Hesabın tarixi

Hesabın tarixi — hesabın görünüşündən tutmuş aksiomlar sistemindən istifadə etməklə ədədlərin rəsmi müəyyənləşdirilməsinə və hesab əməliyyatlarına qədər dövrü əhatə edir. Hesab - ədədlər, onların xüsusiyyətləri və əlaqələri haqqında elm - əsas riyazi elmlərdən biridir. Cəbr və ədədlər nəzəriyyəsi ilə sıx əlaqəlidir.

Hesablama. Pinturikkonun rəsm əsəri. Bordcia mənzilləri. 1492-1495-ci illər. Roma, Vatikan sarayları

Hesabın meydana gəlməsi səbəbi saymağa, sadə ölçmələrə və hesablamalara praktik ehtiyac idi. Hesablama bilikləri haqqında ilk etibarlı məlumatlar eramızdan əvvəl III - II minilliklərə aid Babil və Qədim Misirin tarixi abidələrində tapılmışdır. Hesabın inkişafına dünyanın bütün qanunlarını müəyyənləşdirmək üçün nömrələrdən istifadə etməyə çalışan yunan riyaziyyatçıları, xüsusən də Pifaqorçular məktəbi böyük töhfə vermişdilər. Orta əsrlərdə arifmetikanın əsas tətbiq sahələri ticarət və təxmini hesablamalar idi. Hesab ilk növbədə Hindistan və İslam ölkələrində inkişaf etdi və yalnız bundan sonra Qərbi Avropaya gəldi. XVII əsrdə dəniz astronomiyası, mexanika, daha mürəkkəb kommersiya hesablamaları, hesablama texnikasına yeni hesab sorğuları qoydu və sonrakı inkişafa təkan verdi.

Ədəd anlayışının nəzəri əsasları, ilk növbədə,1889-cu ildə hazırlanmış natural ədədin və Peano aksiomlarının tərifi ilə əlaqələndirilir. Bunlardan sonra,rasional, həqiqi, mənfi və kompleks ədədlərin qəti tərifləri izlənildi. Say anlayışının daha da genişlənməsi,yalnız hesab qanunlarından birini rədd etdikdə mümkündür.

Hesabın yaranması

 

Hesabı göstərən İşanqo sümüklərindəki saylar, Eduard gölü yaxınlığında tapılıb və 30 min ildən çox yaşı var.

İki dəstdə (əşyalar dəsti) bir dəstin hər bir elementinin başqa dəstdə tək cütü olsa,onda bu dəstlər eyni dərəcədə güclüdür. Cisimlər iki sıra düzüldükdə, ibtidai icma quruluşu zamanı ibtidai tayfalar mübadilə olaraq istifadə edildikdə,belə bir faktiki müqayisə obyektlər qrupları arasında kəmiyyət əlaqələri yaratmağa imkan verir və say anlayışını tələb etmir.

Gələcəkdə saymağın təbii standartları, məsələn, barmaqlar, sonra əllər kimi standart dəstlər meydana çıxdı. Xüsusi nömrələri simvollaşdıran standartların meydana çıxması,say anlayışının ortaya çıxması ilə əlaqələndirilir. Cisimlərin sayı göydəki ayla,gözlərin sayı, əldəki barmaqların sayı müqayisə edildi. Daha sonra bir çox standart ən uyğun sayma üsulu ilə ümumiyyətlə barmaq və ya ayaq barmaqlarını saymaqla əvəz edildi.

Növbəti addım konkret cisimlərdən ayrılmış bir natural ədədin ümumi konsepsiyasının ortaya çıxması idi. Natural ədədlər,hüdudsuz bir dəstin sabit və bölünməz obyektlərin (insanlar, qoyunlar, günlər və s.) idealizasiyası kimi,yarandı; müvafiq olaraq, ədədlərlə hərəkətlər,əvvəlcə bu cür dəstlərlə həqiqi hərəkətləri əks etdirirdi(birləşmə, bölmə və s.). Hind-Avropa dilləri üçün, onluq say sistemindən istifadə edərək yüzə qədər daxil olan rəqəmlərin adları artıq yenidən qurulmuşdur. Henri Lebesqyu qeyd edirdi: "İnsanların on bir barmağı olsaydı,on birlik say sisteminin qəbul edilməsi mümkündür".

Hesabın nəticələrini yazmaq üçün bir ağacdan və ya sümüklərdən, iplərdəki düyünlərdən - süni hesab standartlarından istifadə edildi.< Üzərində 55 çərtik olan gənc qurdun mil sümüyü 1937-ci ildə Dolni Vestoniçe (Çexiya) kəndi yaxınlığında tapılmışdır. Tapıntının yaşı təxminən 5 min ildir (digər mənbələrə görə, təxminən 30 min il ),uzun müddət bu ədəd ən qədim bilinən rekord idi. Novosibirskdən olan bir paleolit dövrü mütəxəssisi B. A. Frolov Üst Paleolit dövrünün Dolni Vestoniçe abidələrində qrafik bəzəklərini görür,bu dövrdən etibarən bu dövrün insanlarının eyni elementlərin müəyyən miqdarlarını: 5 və ya 7 , habelə onlardan çox(xüsusən 10 və 14)predmeti ayırd etdiklərini və xüsusilə bəzi miqdarları tez-tez vurğuladığına dair bir çox dəlillər olduğunu deyir.

Rəqəmləri adlandırarkən,ya təyin olunmayan adlardan istifadə edilmişdir (belə ədədlər nodal ədədlər deyilirdi)və ya alqoritmik adlardan istifadə edilmişdir.Üstəlik, alqoritmik ədədlərin birləşməsi nodal ədədlər üzərində aparılan arifmetik əməliyyatlara əsaslanır.

Nömrələmə, habelə nömrələrin adlarının üç prinsipindən birinə əsaslanır:

• aşqar (additio — toplama ) - ${\displaystyle 1,10,100}$  üçün simvol və bu simvolların təkrarlanması (${\displaystyle 1n,10n,100n}$ );
• subtraktiv (subtractio — çıxma) - ədədlərin birləşməsi ${\displaystyle mn}$ ,burada ${\displaystyle m<n}$ , ${\displaystyle n-m}$  fərqinə bərabərdir;
• multiplikativ (multiplicatio — vurma) - ${\displaystyle mn}$  ədədlərin birləşməsi məhsula bərabərdir,Hind -Avropa dillərində, xüsusən də rus dilində on və yüzün adları üçün istifadə olundu.

Yuxarıda göstərilənlərə əlavə olaraq, bir sıra mənbələrdə bölünməyə əsaslanan prinsip də qeyd olunur.

Qədim riyazi mətnlər və say sistemləri

Qədim Misir

 

Rinda papirusunun hissəsi

Misir riyaziyyatı ilə bağlı əsas məlumatlar, Misir mirzəsi Axmesin (e.ə. XVIII-XVII əsrlər) toplusu olan Axmes papirusuna,eləcə də Moskva riyazi papirusuna əsaslanır. Hər iki papirus Orta padşahlıq (Misir) dövrünə aiddir. Yeni padşahlıq , habelə Erkən və Qədim padşahlığın riyazi mətnləri haqqında məlumat qorunub saxlanılmamışdır. Qədim Misirin riyazi papirusları təhsil məqsədləri üçün tərtib edilmişdir, bu papiruslarda tam və kəsr ədədlər üzərində olan köməkçi cədvəllərə,həllərə,arifmetik və həndəsi silsilələrə,həmçinin tənliklərə də rast gəlinir.

Misirlilər onluq say sistemindən istifadə edirdilər. Misir heroqlif yazısı ${\displaystyle 1,10,100,1000}$  və sair on milyona qədər xüsusi simvollarla nömrələnmişdi, bu vaxt heroqlif yazılarda 1-dən 9- dək,onluq,yüzlük,minlik saylar üçün işarələr,həmçinin ${\displaystyle 1/n}$  formalı kəsrlər üçün xüsusi simvollar meydana gəldi.

Misir riyazi mətnlərində problemlərin həlli üsullarının çox asılı olduğu hesablama və buradan ortaya çıxan çətinliklərə xüsusi diqqət yetirilirdi. Misirlilər əlavə olaraq toplama və kəsr kimi arifmetik əməliyyatlardan da istifadə etdilər. Hansısa tam ədədin vurma və hansısa qalıqsız bölmə ikiqat əməliyyatın dəfələrlə təkrarlanması ilə həyata keçirilirdi,bu da ardıcıllığın müəyyən üzvlərinin ${\displaystyle 1,2,4,8,16,...}$  iştirak etdiyi iri həcmli hesablamalara gətirib çıxarırdı. Misirdə yalnız Misir kəsrlərindən istifadə edilirdi və bütün digər kəsrlər Misir kəsrlərinin cəminə parçalandı. Axmes papirusunda ${\displaystyle 2/n}$  forma kəsrli cədvəllər verilib,digər kəsr ilə hesablamalar ikiqat artırılaraq yerinə yetirilmişdir. Bir kvadratın sahəsini, bir kubun həcmini və ya sahəsinə görə kvadratın bir tərəfi misirlilər tərəfindən müəyyən edilərkən,bu əməliyyatların adı hələ alınmamış olsa da,eksponentləşmə və kök çıxarılması əməliyyatları ilə qarşılaşdılar.

Babil

 

${\displaystyle {\sqrt {2}}<math>{\sqrt {2}}\approx 1+24/60+51/60^{2}+10/60^{3}}$ 
= 1.41421296… hesablaması olan Babil cədvəli

Babil mixi yazılı riyazi mətnlərində şumerlərə xas altmışlıq say sistemindən istifadə edilmişdir və bura əsası 60 olan kəsrlər,1-dən 59-a qədər ədədlərin daxil olduğu vurma cədvəlləri, həmçinin mənfi ədədlərin cədvəlləri,natural ədədlərin kvadratı və kubu olan cədvəllər, faiz hesablama cədvəlləri, bazası 60 olan fraksiyalar daxil edilmişdir.Riyazi problemlərin və ədədi cədvəllərin mətnləri ilə zəngin üç yüzdən çox cədvəl məlumdur. Babil üçün cədvəllərin geniş istifadəsi ilə xarakterikdir.

Ardıcıl nömrələmə öncə Babildə meydana gəlir. İlk əlli doqquz ədəd vahid işarələrin təkrarlanması ilə yazılır. Altmış çoxluğu ilk dəstin soluna eyni şəkildə yazıldı. Daha sonra bu tənzimləmə istənilən formada:${\displaystyle 60^{n}}$  və ${\displaystyle 1/60^{n}}$  yayılmağa başladı. Bundan əlavə babillilər ədəd yazarkən sıfır işarəsindən də istifadə etməyə başladılar.

Babildə çıxma və toplama işarələri, onluq mövqelər sistemindəki bu işarələrə bənzər idi ki, sonrakı kateqoriyaya keçid həm sistemin qurulması üçün, həm də vahidlər və onluqlar üçün lazım idi. Babillilər yalnız ${\displaystyle 59}$ -a qədər çox sayda elementin daxil olduğu tək vurma cədvəlindən istifadə etmədilər, ${\displaystyle 1}$ -dən ${\displaystyle 59}$ -a qədər ədədlərin daxil oldduğu ${\displaystyle 1,2,3,...,19,20,30,40,50}$  nömrələrinin böyük hərflərinin istifadə olunduğu məhsul cədvəllərindəndə istifadə olunurdu. Babillilərdə bölmə əməli yox idi,buna görə qarşılıqlı dəyərlər cədvəlinin tərtib edilməsinə, yəni ${\displaystyle 60}$  -ı ${\displaystyle 2,3,4,...}$  -ə bölməklə əmələ gələn ədədlərin hazırlanmasına çox diqqət yetirildi. Bölmə zamanı, sonsuz kəsr verilərkən əvvəlcə mənfi ədədin olmadığı yazılmış və daha sonra təxmini bir dəyər verilmişdir.

Hesab problemlərini həll edərkən, babillilər nisbət və irəliləyişəetibar etdilər. Aritmetik irəliləmənin ${\displaystyle n}$  üzvlərinin cəminin düsturunu, həndəsi irəliləmənin cəmlənməsi qaydalarını bilirdilər,faiz məsələlərini həll edirdilər. Babildə çoxları Pifaqor üçlüyünü bilirdi, onların axtarışı üçün bəlkə də naməlum bir ümumi texnikadan istifadə edilmişdir.Ümumiyyətlə, tənliyin bütöv və rasional həllərini tapmaq problemi ${\displaystyle x^{2}+y^{2}=z^{2}}$  ədəd nəzəriyyəsinə aiddir.. ${\displaystyle {\sqrt {a^{2}+r}}\approx a+{\frac {r}{2a}}}$  qaydasından istifadə edərək,həndəsi tapşırıqlar, kvadrat köklərinin təxmini çıxarılmasına və nəticəni daha da yaxınlaşdırmaq üçün iterativ metodlara ehtiyac duyulurdu

Qədim Yunanıstan

 

Rafael Santi. Pifaqor (Afina məktəbinin təfərrüatı)

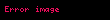
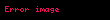
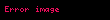
Yunanlar əvvəlcə ${\displaystyle 1,5,10,50,100,500,1000}$  nömrələrinin işarənməsi üçün istifadə edilən Attik say sistemindən istifadə etdilər. Bu sistem eramızın II əsrində qrammatik və tarixçi Eliy Herodian tərəfindən tərtib edilmişdir. Attik nömrələrindən istifadə edərək, abak hesablama lövhəsində hesablamaların nəticələri yazılırdı. Zaman keçdikcə attik rəqəmlər kompakt hərflərlə, yunan rəqəmləri ilə əvəz olumağa başladı. İon say sistemi Yunan əlifbasının 24 hərfindən və üç köhnəlmiş hərflərdən istifadə edilərək ${\displaystyle 1}$ -dən ${\displaystyle 9}$ -a qədər,${\displaystyle 10}$ -dan ${\displaystyle 90}$ -a qədər və ${\displaystyle 100}$ -dən ${\displaystyle 900}$ -ə qədər yüzlərlə (dövriyyədən çıxan hərflər ${\displaystyle 6,90,900}$  rəqəmlərini bildirmək üçün istifadə olunurdu) olan vahidləri göstərdi. Rəqəmləri yuxarıdakı hərflərdən ayırmaq üçün bir xətt qoyurdular. ${\displaystyle 1000}$  rəqəmini yazmaq üçün eyni simvoldan istifadə edilirdi,yalnız sol tərəfdən alt hissədə ştrix qoyulurdu. Bu mövqeli say sisteminə bənzəyirdi,amma ona tam olaraq keçid baş vermədi. Belə bir sistemin hesabı çətinləşdirdiyini,lakin, 1882-ci ildə, fransız riyaziyyat tədqiqatçısı Pol Tanneri, düzgün yanaşma ilə Yunan say sisteminin hesablama sürətində onluq sistemindən çox fərqli olmadığı qənaətinə gəldi.

Qədim yunan arifmetikasının inkişafı Pifaqorçular məktəbi ilə əlaqələndirilir.Onların fikrincə, bütün maddi və mənəvi şeylər və anlayışlar əslində rəqəmlərin obrazlarıdır, onlarla eynilik təşkil edirlər. Eyni zamanda rəqəmlər həndəsi mənada anlaşılırdı. Nöqtə vahiddir, iki nöqtədən düzxət alınır, üç nöqtə artıq müstəvidir.Beləliklə, rəqəmlər Pifaqor məktəbində universal obyektlərdir. Onlar təkcə riyazi deyil, həm də həqiqətin çoxluğunun göstəricisidir. Onlara görə hər şeyin, o cümlədən mənəvi məsələlərin də riyazi mahiyyəti vardır. Xüsusilə, pifaqorçu Arxitas (Tarentli) yazırdı: "Hesablama, fikrimcə, biliklərin təkmilləşdirilməsi üçün digər elmlər arasında fərqlənir; və həndəsədə daha mükəmməldir, çünki hər hansı bir mövzunu həndəsədən daha aydın bir şəkildə araşdırır".

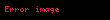
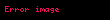
Pifaqorçular "fiqurlu ədədlər"in ("üçbucaqlı", "kvadrat" və digərləri) tərifi ilə xarakterizə olunur. Ədədlərin xüsusiyyətlərini öyrənərək, onları tək və cüt (ikiyə bölünmə əlaməti olaraq), sadə və mürəkkəb hala gətirdilər. Çox ehtimal ki, yalnız bölmə nişanından istifadə edərək Pifaqorçulular sübut edə bildilər,${\displaystyle 1+2+...+2^{n}=p}$  — sadə ədəddir, onda ${\displaystyle 2^{n}p}$  — mükəmməl ədəddir. Sübut Evklidin "Başlanğıcları" nda göstərilmişdir (IX, 36), yalnız XVIII əsrdə Leonard Eyler başqa mükəmməl ədədlərin olmadığını sübut etdi və mükəmməl ədədlərin sayının sonsuzluğu məsələsi hələ həll edilməmişdir. Pifaqorçular da bir düstur əldə etdilər və ${\displaystyle x^{2}+y^{2}=z^{2}}$ , sözdə Pifaqor üçlüyü tənliyinin sonsuz sayda tam həllini tapdılar.(Pifaqor üçlüsünün müəyyənləşdirilməsi üçün ilk düsturun nəticəsi hesab və ya ədədlər elminə çox diqqət yetirən Platona aid edilmişdir.).

Məlumdur ki, Pifaqorçuar arasında rasional ədədlər və ya parçaların əlaqələri doktrinası mövcud idi,lakin özü qorunub saxlanılmamışdır. Eyni zamanda,vahid kvadratın tərəflərinin diaqonalının uyğunsuzluğunun sübutlarına sahibdirlər. Bu kəşf tam ədədlərin əlaqəsinin istənilən parçaların əlaqələrini ifadə etmək üçün yetərli olmadığını və bunun əsasında metrik həndəsə qurmağın mümkün olmadığını ifadə etdi. İrrasionallığın ilk doktrinası Sokratın tələbəsi Afinalı Teetetə məxsusdur.O sahəsi kvadrat olmayan tam ədəd kimi ifadə edilən bir kvadrat üçün,tərəf vahid kvadratın yan tərəfi ilə ölçülməz olduğunu müəyyən etdi,başqa sözlə, 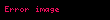${\displaystyle {\sqrt {N}}}$  formasının irrasionallığını müəyyənləşdirdi, bənzər bir şəkildə,vahid kub üçün ${\displaystyle {\sqrt[{3}]{N}}}$  formasının irrasionallığını təyin etdi.

Ümumi bölünmə nəzəriyyəsi e.ə. 399-cu ildə ortaya çıxdı və yəqin ki, Teeteteyə aiddir. Evklid ona "Başlanğıclar" ın VII və IX kitablarını həsr etmişdi. Nəzəriyyə iki ədədin ən böyük ortaq böləninin ƏBOB un tapılması üçün Evklid alqoritminə əsaslanır. Alqoritmin nəticəsi,istənilən sayın sadə amillərə parçalanma ehtimalı, eləcə də belə bir parçalanmanın bənzərsizliyidir. Faktorlaşmanın vahidliyi qanunu tam ədədlərin hesabının əsasını təşkil edir. Evklid alqoritmi rasional ədədin qismən parçalanmasını davamlı kəsrə təyin etməyə imkan verir. Ancaq Qədim Yunanıstanda davamlı kəsr anlayışı yaranmadı.

Evklidin ardınca,rasional ədədlər üçün, tam ədədlərdən fərqli olaraq bölmə həmişə mümkündür. Yunanıstanda ${\displaystyle m/n}$  formalı kəsrləri necə idarə etməyi bilirdilər: onları toplaya,çıxa, ortaq məxrəcə gətirə bilir,vura və bölə, həmçinin ixtisar apara bilirdilər. Nəzəri quruluşlarda yunanlar bir bölünməzliyə əsaslandılar və vahid kəsrlər haqqında deyil,tam ədədlərin nisbəti haqqında danışdılar. Bu münasibətlər üçün mütənasiblik anlayışı müəyyən edildi, bütün münasibətləri boşaldılan siniflərə çevirdi. Qədim Yunanıstanda, eyni əlaqələrə sahib olanların ən kiçik cütü və ya rəqəmlərin qarşılıqlı olduğu cütlük təyin edildi,bu da, azalmayan kəsrlər anlayışına uyğundur.

Son ölçülərin qurulması və həqiqi sayların müəyyən edilməsi problemləri e.ə. V əsrdə elmi böhranın üzərinə düşdü,hansı ki,buna Qədim Yunanıstanın bütün fəlsəfi məktəbləri cəlb edildi. Bu problemlərin həllində rast gəlinən bütün çətinliklərin həllinə,Eleyalı Zenonun paradokslarında və ya aporialarında müvəffəq olundu. Riyaziyyatın yeni əsaslarını Knidli Evdoks təklif etdi. Həndəsi kəmiyyət haqqında daha çox ümumi bir konsepsiya - məsələn parça, sahə, həcm hazırladı. Bərabər çoxluqlar üçün Evdoks, aksiomlardan istifadə edərək çoxluqlar münasibətləri nəzəriyyəsini müəyyənləşdirdi və eyni zamanda Arximed aksiomu olaraq bilinən aksiomu təqdim etdi.Bu yanaşma çoxluqların ixtiyari əlaqələrini təyin etməyə imkan verdi,o zaman məlum olan uyğunsuzluq problemlərini həll etdi.Bununla belə,Knidli Evdoks davamlılıq aksiomunun analoqunu yaratmadı,bunun üçün uyğunluq məsələsi tam həll edilmədi.Evdoks da çoxluqlar üçün hesab əməliyyatlarını təyin etməmişdir. Nəhayət say və kəmiyyət anlayışlarını (daha doğrusu, kəmiyyətin vahid standartına nisbəti) İsaak Nyuton "Universal Hesab"ında (1707) birləşdirdi. Eyni zamanda, Evdoksun quruluşları, Riçard Dedekind tərəfindən verilən həqiqi ədədlər nəzəriyyəsinin sonrakı tərifinə o qədər yaxındır ki,Rudolf Lipsçitz məktublarının birində ondan yeni nə etdiyini soruşdu.

Makedoniyalı İskəndərin fəthlərindən sonra Yunan elminin mərkəzi İsgəndəriyyəyə köçdü. O dövrün əsas işi on üç kitabdan ibarət Evklidin "Başlanğıclar" əsəri idi. V kitab Evdoksun münasibətlər nəzəriyyəsinə, VI kitabı - parçaların vurulması və ya paraleloqramların qurulması ilə əlaqələrin qurulması, VII-IX kitablarda parça kimi qəbul olunan tam ədədlər və rasional ədədlər nəzəriyyələri,X kitab - Afinalı Teetetəyə görə irrasionalların təsnifatına həsr olunmuşdur.

 

Diofantın "Hesab" ından (XIV əsrin əlyazması) vərəq. Üst sətirdə aşağıdakı tənlik var::${\displaystyle x^{3}\cdot 8-x^{2}\cdot 16=x^{3}}$ 

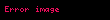
Arximedin "Psammit" əsərində ixtiyari böyük sayları ifadə etmək üçün bir üsul hazırlanmışdır. Onun qurulması (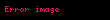${\displaystyle 10^{8}}$ -ə qədər) birinci dərəcəli ədədlərin qurulmasına, sonra (${\displaystyle 10^{8}}$ -dən ${\displaystyle 10^{8}\cdot 10^{8}}$ -ə dək) ikinci sıraya imkan verir və bu,daha sonra davam etdirilə bilər. Arximed həmçinin göstərir ki, diametri Yer kürəsindən ${\displaystyle 10000}$  dəfə az olan bir sferadakı qum dənələrinin sayı ${\displaystyle 10^{63}}$ -dən çox deyil, başqa sözlə, sonludur.

Gələcəkdə, ümumiyyətlə riyaziyyat kimi qədim yunan hesabı da tənəzzülə doğru getdi. Yeni bilik eramızın yalnız I-II əsrlərdə meydana çıxır. III əsrdə İskəndəriyyəli Diofant həndəsəyə əsaslanmayan,hesaba əsaslanan cəbr qurmağa başladı. Diofant ayrıca say sistemini mənfi ədədlərə qədər genişləndirdi. Diofantın rasional ədədlərdə qeyri-müəyyən tənliklərin həlli,say nəzəriyyəsi və cəbr həndəsəsinin qovşağı üzərində işləyir.

Qədim Roma

Rum rəqəmləri hesablama sistemi üçün az uyğunlaşdırılmışdı. Rum rəqəmləri əlifbadan öncə yaranmışdı və onun hərflərinə uyğun gəlmir. Əvvəlcə 1-dən 9-a qədər olan rəqəmlərin müvafiq şaquli çubuklarla işarələnir və onların kəsişməsi sayın on qat artması demək idi(X sayı kimi).Buna görə 100 sayını əldə etmək üçün çubuq iki dəfə kənara çəkilirdi. Sonradan sistemin sadələşdirilməsi baş verdi. Hal-hazırda xüsusi hallarda - XIX əsr,VI qurultay və s. istifadə olunur.

Çin

 

Tusi-Paskal üçbucağı Çin orta əsr əlyazmasında, 1303-cü il

Eramızın II əsrində - Çinin bizə gələn bütün riyazi əsərlərindən ən qədimi "Ölçü Qütbü haqqında traktat" (astronomiya haqqında) və "Doqquz kitabda riyaziyyat" (torpaq tədqiqatçıları, mühəndislər, rəsmi şəxslər və ticarətçilər üçün bir kitab) adlı risalə yaradıldı. III-IV əsrlərdə yazılmış bir sıra kitablarla birlikdə uzun müddət dəyişiklik edilmədən yenidən çap olunan "On klassik traktatı" meydana gətirdilər. XIV əsrə qədər Çin riyaziyyatı hesablama lövhəsində həll edilməsi üçün hesablama alqoritmləri toplusu idi.

Çin nömrələri vurma prinsipinə əsaslanır: rəqəmlər yuxarıdan aşağıya və ya soldan sağa yazılır, min ədədi üçün min işarəsi, sonra yüz ədədi üçün yüz işarəsi,on ədədi üçün on işarəsi və nəhayət vahidlərin sayı göstərilir. Hesab əməliyyatlarını yerinə yetirmək üçün bir sayma lövhəsi, suanpan hesablayıcısı və sayma çubuqlarından istifadə edilirdi.Üstəlik, III əsr Çin riyaziyyatçısı Sun Tszıya görə, "adi hesablamada istifadə olunan metodlarda,ilk növbədə sıralarla tanış olunmalıdır: ədəd şaquli, onlar üfüqi; yüzlər durur, minlər yatır; minlərlə və yüzlər eyni görünür, on minlərl və yüzlər də həmçinin"..

Hesablama lövhəsində yerinə yetirilən toplama və çıxma əməliyyatları əlavə cədvəl tələb etmirdi, ancaq vurma üçün ${\displaystyle 1\times 1}$ -dən ${\displaystyle 9\times 9}$ -a qədər vurma cədvəli vardı. Vurma və bölmə əməliyyatları ən yüksək rəqəmlərdən başlayardı,bunun üçün yoxlamanı mümkünsüz edən aralıq nəticələr lövhədən çıxarıldı.Əvvəlcə vurma və bölmə müstəqil əməliyyatlar idi, lakin sonra Sun Tszı onların qarşılıqlı tərsini qeyd etdi. Kəsrlər tam ədədlərlə demək olar ki, eyni vaxtda, e.ə.II əsrə qədər meydana gəldi,eramızda kəsr əməliyyatları yaxşı işlənmişdi. Toplama və çıxma üçün məxrəclərin sayından istifadə edildi,vurma həndəsi olaraq düzbucağın sahəsi kimi təyin olundu, bölmə bölmə ilə bağlı tapşırıqlar ilə əlaqəli idi, bölgüdə iştirak edən saylar kəsr ola bilərdi. V əsrdə Çjan Tsyu-tszyan vurma ilə bölməni alt-üst kəsr ilə əvəz etdi,kəsr bir cüt say olaronluq kəsrlər görünür,onların köməyi ilə irrasional kəmiyyətlərin təxmini dəyəri verilirdi.

Çində, avropalıların hind elminə aid etdiyi iki saxta müddəanın qaydasından istifadə edərək problemləri necə həll edəcəyini bilirdilər. Sağdakı ${\displaystyle ax-b=y}$  tənliyinin sol tərəfindəki iki fərqli dəyəri əvəz etməklə iki fərqli dəyər alınır, bunlardan nisbətdən istifadə edərək ${\displaystyle ax-b=0}$  üçün bir həll tapmaq mümkün idi. Çinlilər sağ tərəfdəki artıqlıq və çatışmazlıq olduqda bu seçimdən istifadə etdilər. Xətti tənliklər sistemini həll etmək üçün mənfi ədədləri tətbiq etmək lazım idi. Lövhədə fərqli rəngli çubuqlar ilə, məktublarda çəp xüsusiyyətləri ilə fərqlənirdilər. Bundan əlavə, mənfi ədədlərin xüsusi bir adı var idi. Onlar üçün toplama və çıxma əməliyyatları aparmaq qaydaları tərtib edildi,üstəlik, çıxma ilk növbədə müəyyən edildi. Əvvəlcə mənfi ədədlır yalnız hesablama prosesində istifadə edildi və hesablamaların sonunda lövhədən çıxarıldı,sonra Çin alimləri onu borc məsələlərində,bir çox çatışmamazlıqda istifadə etməyə başladılar.  

Orta əsrlərdə hesab

Hindistan

Mövqeli say sistemi Hindistanda (on rəqəmi, o cümlədən sıfır) tətbiq edilmişdir. Hesab əməliyyatlarını yerinə yetirmək üçün nisbətən sadə qaydaların hazırlanmasına imkan verdi. Alimlər hesab edirlər ki, mövqeli say sistemi ilk dəfə Hindistanda eramızın əvvəlindən gec olmayaraq yaranıb. Ancaq hindlilər yazı üçün kövrək materiallardan istifadə etdiklərinə görə,bu dövrün sənədli abidələri yoxdur. Mövqe nömrələməsindən istifadə edərək orijinal sənəd,XII əsrə aid olduğu hesab olunan Baxşali əlyazması^[en]  hesab olunur.

 

Puna Astronomiya və Astrofizika mərkəzindəki Ariabhata heykəli

Hindistanda tam ədədlər üçün onluq sistemindən istifadə edilmişdir. Əvvəlcə bunlar sağdan sola yazılan Xaroşti məktubundakı, sonra isə soldan sağa yazılan Brahmi məktubundakı ədədlər idi. Hər iki variant da 100-ə qədər ədədlər üçün toplama əməlindən və vurma əməlindən istifadə edildi. Yalnız brahmidə 1-dən 9-a qədər olan nömrələr üçün xüsusi işarələrdən istifadə olunurdu. Bu sistemin əsasında Devanaqari yazılarının müasir rəqəmləri (və ya "ilahi məktublar") hazırlanmışdır,onluq mövqelər sistemində istifadə olunmağa başlandı. 595-ci ilə, doqquz rəqəmin tətbiq olunduğu yazının ilk qeydi aiddir, o zaman hələ sıfır yox idi. Hesablamaların rahat aparılması üçün Ariabhata, Sanskrit yazılarının işarələri ilə nömrələri yazmağı təklif etdi. 662-ci ildə Suriyanın Şimali Seboht xristian yepiskopu yazdı: "Mən hindlilərin elminə toxunmayacağam ... bütün təsvirlərdən üstün olan onların say sistemidir. Hesabda doqquz simvoldan istifadə edildiyini sadəcə demək istəyirəm." .

Hindistanda əsas hesablama əməliyyatları toplama,çıxma,vurma, bölmə, kvadrat və kub hesab edildi, qaydaların inkişaf etdirildiyi kvadrat və kub köklərinin çıxarılması nəzərdən keçirildi. Hesablamalar qum və ya toz ilə bir hesablama lövhəsində və ya sadəcə yerdə aparılırdı və bir çubuqla qeyd edildi. Aralıq hesablamalar silindi, bu, doqquzdan istifadə edərək yoxlamadan istifadə edərək əks əməliyyatdan istifadə edərək yoxlamanı qeyri-mümkün etdi. Hindlilər kəsrləri bilirdilər və üzərində əməliyyatlar, nisbətlər, ədədi silsilələr edə bilirdilər. Artıq eramızın VII əsrindən mənfi ədədlərdən istifadə edərək, borc, həm də irrasional ədədlər kimi şərh etdilər. Ədədlər sırasını yekunlaşdırdılar,xüsusilə, Vedalarda hesab və həndəsi silsilələr nümunələri mövcuddur və XVI əsrdə Narayana Pandit^[en]  daha ümumi ümumiləşdirmələr etmişdir.

Hindistanlı riyaziyyatçılar Ariabhat, Brahmaqupta və Bhaskara, ${\displaystyle ax+b=cy}$  formasının Diofantin tənliklərini tam ədədlərlə həll etdilər. Bundan əlavə, onlar ${\displaystyle ax^{2}+b=y^{2}}$  formasının tam tənliklərini həll etdilər,bu hind riyaziyyatçıların say nəzəriyyəsi sahəsində ən yüksək nailiyyəti idi. Sonradan bu tənlik və ${\displaystyle b=1}$ -dəki xüsusi hadisəsi Pyer Ferma, Leonard Eyler və Jozef Lui Laqranjın diqqətini çəkdi. Laqranja tərəfindən təklif olunan həll yolunu tapmaq üsulu,hindlilərə yaxın idi.

İslam ölkələri

IX-X əsrlərdə İslamın elmi mərkəzi Bağdad idi, burada Əl-Xarəzmi, Həbbəş əl-Həsib, Əl-Fərqani, Sabit ibn Kurra, İbrahim ibn Sinan, Əl-Battani çalışırdılar. Daha sonra İbn Sina, Əl-Biruni və Əbu Kamilin işlədiyi Buxara, Xarəzm və Qahirədə, daha sonra Ömər Xəyyam və Nəsirəddin Tusinin işlədiyi İsfahan və Marağada yeni elmi mərkəzlər yarandı. XV əsrdə Səmərqənddə yeni bir elmi mərkəz yaradıldı, burada Qiyasəddin Cəmşid çalışdı. Afrikanın şimal-qərb sahilləri və Pireney yarımadasının riyazi mərkəzləri biliklərin Avropaya yayılmasında böyük rol oynadı.

 

"Hindistan hesabı haqqında" latın dilli tərcümədən bir səhifə

Ərəblərdə iki növ nömrələmə vardı: hərfi və onluq mövqelər. Hərfi nömrələmə qədim yunan hərfinə bənzəsə də, qədim semit əlifbasına keçir. IX əsrin əvvəllərində Məhəmməd ibn Musa əl-Xarəzmi "Hindistan hesabı haqqında" bir kitab yazdı. Dərslikdə "müxtəlif növ və dərəcələrin" praktik problemlərinin həlli mövcuddur və mövqe say sistemindən istifadə edərək yazılmış ilk kitab idi; bundan əvvəl nömrələr yalnız hesablama lövhəsində hesablama üçün istifadə olunurdu. XII əsrdə Adelard (İngiltərə) və Con Sevelski (İspaniya) kitabın latın dilinə iki tərcüməsini etdilər. Əsli qorunmamışdı, lakin 1857-ci ildə, "Hindistan ədədi haqqında Alxorezm" in latın dilinə tərcüməsi tapıldı. Traktatda toplama,çıxma,vurma, öz-özünə vurma, bölmə və kvadrat kökünün çıxarılması kimi hesablama əməliyyatların sayma lövhəsində hind ədədlərindən istifadə edilmək təsvir olunur.Kəsr çoxalması, bölünmə kimi, nisbətlərdən istifadə edərək hesab edildi: ${\displaystyle a}$  ilə ${\displaystyle b}$ -yə vurmaq ${\displaystyle q}$ -ı tapmağa bərabər idi ki, ${\displaystyle q:a=b:1}$ . Bu nəzəriyyə ərəb arifmetikasının əsası idi. Bununla birlikdə kəsrlərin başqa bir hesablaması var idi,hər hansı bir kəsri alikvot kəsrlərin cəmi kimi təmsil edirdi.

952-953-cü illərdə Əbu l-Həsən Əhməd əl-Uklidisi özünün "Hindistan arifmetikasına dair kitablar" əsərində tək ədədləri yarıya bölmək və digər hesablamalar zamanı onluq kəsrlərdən istifadə etdi, lakin bu kitab sonrakı inkişafa təsir etmədi. XV əsrin əvvəllərində əl-Kaşi bütün əməliyyatları tam ədədlərlə həyata keçirən və "astronomların hesablamasını" bilməyənlər üçün mövcud olan kəsr sistemini qurmağı planlaşdırırdı.1427-ci ildə əl-Kaşi onluq sistem təsvir etdi, 1585-ci ildə Simon Stevin yazılarından sonra Avropada geniş yayıldı. Beləliklə, əl-Kaşi kəsrlərın əsas qaydalarını tərtib etdi,onları altmışlıq say sisteminə və əksinə çevirmək üçün düsturlar hazırladı.

Əl-Xarəzminin əsərlərinə kvadrat kök çıxartma metodu, Kuşyar ibn Labbana kub kökləri çıxarmaqla məşğul olmuş, Ömər Xəyyam köklərin hesablanması metodlarının ümumi inkişafı ilə məşğul olmuşdur. "Lövhələr və tozun köməyi ilə hesablama toplusu" (1265) əsərində Tusi hər hansı bir dərəcənin kökünü tam bir ədəddən çıxartmağın izahını vermişdir. Sxem əslində XIX əsrdə təklif olunan Hörner sxemi ilə üst-üstə düşür,kökün kəsr hissəsi ${\displaystyle {\sqrt[{n}]{a^{n}+r}}}$ ,təxminən ${\displaystyle {\frac {r}{(a+1)^{n}-a^{n}}}}$  şəklindədir. Bundan əlavə,Tusi,Paskal üçbucağına bənzər Tusi-Paskal üçbucağında binomial əmsalların üçbucaq formasında düzülüşü cədvəlini verir. Ərəb ölkələrində diqqət daha çox irrasional ədədlərə və təxmini hesablamalara verilirdi. Əl-Xarəzmi qədim Yunanıstanda istifadə olunan ölçülməz seqmentlərdən daha çox,kökaltılarla sadə əməliyyatlar etdi. Nisbətlər nəzəriyyəsi tənqidi təhlildən keçdi. Xüsusilə, Ömər Xəyyam 1077-ci ildə "Evklid kitabının təqdim edilməsindəki çətinliklər haqqında şərhlər" traktatında qədim yunan tərifinin nisbətlərin əsl mahiyyətini əks etdirmədiyini söylədi. Xəyyam nisbətin yeni tərifini verdi, "daha çox" və "daha az" əlaqəsini təqdim etdi, müsbət həqiqi ədədlər anlayışını ümumiləşdirdi. Mənfi ədədlər ərəb riyaziyyatçıları arasında məşhur deyildi.

Məsələləri həll etmək üçün ərəblər Hindistandan gəlmiş nisbəti istifadə etdilər və Əl-Biruni tərəfindən "Hindistan Rəşiklərinin Kitabındakı" bir sıra digər tövsiyələr ilə birlikdə, Çindən gəlmiş və Kust ibn Luccanın "İki yalnış mövqe qaydası kitabı" nın nəzəri əsaslandırmasının iki saxta müddəası təsvir edilmişdir.

Sayı nəzəriyyəsində İslam elminin uğurları az əhəmiyyət kəsb etmir. Tam ədədlərdə birinci və ikinci dərəcəli tənliklərin necə həll olunacağını bilirdilər, Tusi-Paskal üçbucağının qurulması qaydalarını bilirdilər və ilk dəfə bunu da bildirirdilər ki, ${\displaystyle x^{3}+y^{3}=z^{3}}$  tənliyi Böyük Ferma teoreminin xüsusi bir hadisəsi olan rasional ədədlərdə həll edilə bilməz. Bu ifadənin yuxarıdakı dəlilləri qorunub saxlanılmadı.

Bizans

İlk Bizans xristian riyaziyyatçısı VI əsrdə yaşamış Anfimiy idi. Bizans hesab sisteminə ərəb və qədim yunan riyaziyyatçılarının əsərləri təsir etmişdir. XI əsrdə yaşamış Mixail Psell, hesablama sistemi mövzusunda esseyə sahibdir; bu esse rəqəmlərin və əlaqələrin təsnifatına aiddir və ${\displaystyle x^{5}}$  "ilk görünməz" və ${\displaystyle x^{7}}$  - "ikinci əlçatmaz" deyərkən dərəcə adlarını verir. Psell, əvvəllər olduğu kimi eksponentlərin məhsul ilə ifadə edildiyi bir vurma sistemini bildiyini və istifadə etdiyini qeyd edir. XIII əsrdə yaşamış Maksim Planud;Diofantınn "Arifmetikasına",habelə "Hindistanda modelləşdirilən arifmetikadakı" şərhlər verdi. XIV əsrdə John Pediasim, çətin suallarını vurğulayaraq, arifmetikaya dair bir neçə esse yazdı, Nikolay Ravda barmaqlarda hesablama metodu və kvadrat kökləri çıxartmaq üçün təxminən bir üsul verdi və Isak Arqir, Evklidin "Başlanğıclarının" ilk altı kitabını şərh etdi və altıbucaqlı kəsrlərdən istifadə edərək 102-ə qədər ədədlər üçün kvadrat kökləri çıxartma cədvəlini qurdu..

Amerika

 

Arifmetik hesablamalar üçün yupanadan istifadə edildi

Mərkəzi Amerikada əsasən iyirmilik say sistemindən istifadə olunurdu. Yukatandan olan Mayya kahinləri,onu süni şəkildə yaratdı və təqvim hesablamalarında istifadə etdi. Bu, ikinci kateqoriya natamam idi və yalnız ${\displaystyle 19}$ -a çatdı. Əlavə bir səbəb olaraq,${\displaystyle 5}$  sayı da istifadə edilmişdir. Maya təqvimi bir mövqe sistemi idi,burada hər mövqedə müəyyən sayda əlaməti olan bir tanrı var idi. Yazarkən, tanrılar təsvir olunmurdu və boş bir yeri göstərmək üçün,açıq bir boşluq və ya göz simvolu istifadə edildi.Cənubi Amerikada sayları qeyd etmək üçün ədədlərdən və ya kipudan istifadə olunurdu.

Arifmetik hesablamalar abakusun analoqu olan yupanadan istifadə edilərək aparıldı, lakin say sisteminin özəlliklərinə görə, astronomik hesablamalarla əlaqəli olmayan arifmetika zəif inkişaf etdirildi.

Qərbi Avropa

Qərbi Avropada erkən feodalizm dövründə elmə ehtiyac praktik hesab və həndəsə məsələlərindən də yan keçmədi. Kitablarda yeddi sərbəst sənət haqqında,hesab da daxil olmaqla əsas məlumatlar var. Ən məşhurları VI əsrə aid Boesiusun yazıları idi,digərləri ilə, Nikomaxusun (Gerasalı) "Arifmetik ilahiyyatını" öz say nümunələri ilə latın dilinə və dəqiq sübutlar olmadan Evklidin "Başlanğıcları" nın bir hissəsini tərcümə etmişdir.

XX əsrdə İspaniya və Siciliya vasitəsilə ərəb dünyası ilə elmi əlaqələr qurulmağa başladı. Bu zaman daha sonra Papa II Silvester olan rahib Oriyakalı Herbert Kataloniyada oldu. "Nömrələrin bölünməsi haqqında kitab" və "Abak hesab qaydaları" kimi əsərlər ona aiddir. Hər iki kitabda ədədlər sözlə və ya Rum rəqəmləri ilə yazılmışdır. Herbert abak lövhəsi üzərindəkiləri hesablayıcılar adlandırdı.

 

Fibonaççinin "Abak kitabı" ndan səhifə

XII-XIII əsrlərdə hesaba dair ərəb ərəb kitablarının latınca tərcümələri Avropada meydana gəldi. Əsas tərcümələr arxiyepiskop I Raymondun himayəsi altında Toledo şəhərində,Pireney yarımadasının ərazisində, həmçinin Barselona və Seqoviyada ərəb dilindən edilmişdir. Kitablarda onlu nömrələmənin tərəfdarları latınca riyaziyyatçı Əl-Xarəzmi adı ilə "Alqoristlər" adlandırmağa başladılar. Tədricən yeni sistem üstünlük təşkil etdi. Onun əsas üstünlüyü hesab işlərinin sadələşdirilməsi idi. Ancaq Almaniyada, Fransada və İngiltərədə XV əsrin sonlarına qədər yeni rəqəmlərdən istifadə edilmədi.

Sonrakı tərcümələr XIII əsrdə yaşayan italiyalı Leonardo Fibonaççi(Pisano və ya Pizalı) tərəfindən aparılmışdır. 1202-ci ildə yazılmış əsas əsəri "Abak kitabı"nda, hind ədədlər sistemini müdafiə etdi və abakist tətbiqləri doğru yoldan sapma hesab etdi. Fibonaççi sıfırdan həqiqi ədəd kimi istifadə etdi, doqquzu istifadə edərək bir yoxlama etdi,2, 3, 5, 9 ilə bölünmə əlamətlərini bilirdi,məxrəci azolan kəsrdən istifadə edərək kəsrlərin ortaq məxrəcə gətirilməsini,nisbəti təyin etdi, beş, yeddi, doqquz miqdar saylarından istifadə edərək digər nisbət və tənasüb qaydalarını izah etdi,sıraları cəmləşdirməklə idarə olunan qarışdırma problemlərini həll etdi,əks sıralar və ya Fibonaççi ədədləri daxil olmaqla,kvadrat və kub köklərinin təxmini hesablanması üsullarını izah etdi. "Abak kitabında" sonrakı riyaziyyatçıların əsərlərində geniş istifadə edilmiş müxtəlif üsullar sübut ilə birlikdə təqdim olunmaqla yanaşı tapşırıqlarda verilmişdir.

Daha sonra Kenterberi kafedralı arxiyepiskopu olmuş Oksford Universitetinin müəllimi Tomas Bradvardin (XIV əsrin əvvəlləri),Boesiusun "Arifmetik ilahiyyat" əsərinin qısaldılmış versiyasını,"Nəzəri həndəsə" kitabını yazır.Bundan əlavə, bu mütəfəkkir mexanika ilə əlaqədar işində "yarım" münasibətdən istifadə etdi,fransız riyaziyyatçısı Nikola Orem "Sfera haqqında traktat" adlı əsarində kəsr eksponentləri nəzəriyyəsini inkişaf etdirdi,həm də kifayət qədər yaxın tam ədədlər və kəsr ədədləri arasında bağlana bilən və müsbət kəsr göstəriciləri ilə bir gücə yüksəldilə bilən irrasional göstərici anlayışına yaxınlaşdı,kəsr üstlü qüvvət anlayışını daxil etdi. Oremin əsərləri yalnız XIX əsrdə nəşr edilmişdir.

 

Flamand nəşrinin "Onuncu"nun baş səhifəsi

1484-cü ildə Fransız Tibb Bakalavrı Nikola Şyukenin "Ədədlər haqqında üç hissədən ibarət elm" əsəri nəşr olundu,ilk dəfə məchulun dərəcəsini göstərmək üçün qüvvət üstündən istifadə etmişdir. 1487-ci ildə Luka Paçoli hesab əməlləri qaydalarını, bəzi cəbri tənliklərin həllərini, həndəsi mütənasiblik nəzəriyyəsini şərh etmişdir. "Hesab, həndəsə, nisbət və mütənasibliyə dair biliklərin cəmi" dərsliyinin müəllifidir. 1494-cü ildə Venesiyada nəşr olunan bir kitabda, Paçoli, cəbr simvollarından istifadə edərək müxtəlif hesablama metodlarını göstərmişdir. Paçoli toplamanı — ${\displaystyle {\tilde {p}}}$ ,cıxmanı isə — ${\displaystyle {\tilde {m}}}$  ilə işarələdi. Bundan əlavə, mənfi ədəd üçün "sıfırdan az" ifadəsini istifadə etdi və ədədləri çoxaltdıqda işarələrin dəyişəcəyi qaydasını hazırladı.

Cerolamo Kardanonun "Böyük sənət" əsərində XVI əsrdə xəyali kəmiyyətlər və ya sofizm anlayışını təqdim edildi. Kub tənliyin həll düsturu onun adı ilə bağlıdır. Kardanonun özü bunları yararsız hesab etsə də, Raffaele Bombelli tərəfindən kub tənliklərini həll etmək üçün istifadə olunurdu, xəyali və həqiqi ədədlərin çoxalma qaydalarını da təqdim etdi. Raffaele Bombelli "Cəbr" (1572-ci il) əsərinin müəllifidir,ilk dəfə riyaziyyata kompleks ədədlər anlayışını daxil etmişdir. Eyni əsrdə Avropada onluq kəsrlər yayıldı. Bunlar Fransua Viyet, İmanuel Bonfis, Simon Stevinin əsərlərində görünürlər. 1585-ci ildə "Onuncu" kitabında onlar onluq kəsrlərin geniş yayılması üçün təşəbbüs göstərdilər. Elə həmin il "Arifmetik" əsərində "hər şeyin miqdarı ifadə olunan köməyi ilə" irrasional ədədlər kökünün yeni tərifini verdi. Stevin irrasional və qismən mənfi ədədləri kəsrlər kimi həqiqi saydı,ayrıca bölünən vahid hesab edildi.

Mixel Ştifel "Tam hesab" kitabının müəllifidir,o, kitabda onun yazıldığı dövrdə hesab əməlləri, məchul və onun qüvvətlərinin işarələnmələrində aparılan bütün dəyişikliklər öz əksini tapmışdır; kvadrat kökləri işarə etmək üçün simvol daxil etmişdir,ədədi silsiləni mənfi ədədlər obastına genişləndirmiş, həndəsi silsilədə isə mənfi üstlü qüvvət daxil etmişdir. 1569-cu ildə Aristotelin tənqid etdilməsi kralın verdiyi sərəncamla qadağan edilmiş fransız professoru Pyer de la Rame "Otuz bir kitabda riyaziyyat kursu" əsərini yazdı,riyaziyyata həndəsəyə deyil,hesaba əsaslanan yeni bir əsaslandırma verməyə çalışdı.

Yeni dövr hesablaması

XVII əsrdə astronomik naviqasiya, mexanika və daha mürəkkəb kommersiya hesablamaları hesablama texnikasına yeni tələblərlə hesabı təqdim etdi,sonrakı inkişafa təkan verdi.

Onluq hesab və say anlayışının genişləndirilməsi

Say anlayışı əhəmiyyətli dəyişikliyə uğradı. Əvvəllər yalnız müsbət rasional ədədlər ədədlər sahəsinə aid edilirdisə, XVI əsrdən bəri irrasional və mənfi ədədlər getdikcə daha çox tanınırdı. 1637-ci ildə Rene Dekartın "Həndəsə" sində hesab və həndəsi quruluşlar arasında əlaqə qurulur,üstəlik, ədədi coxluqlar, Evkliddəkindən fərqli olaraq, ölçüsünü itirir və həndəsədən ayrılır. Hər hansı bir kəmiyyətin vahid standartına nisbəti bu vəziyyətdə həqiqi ədədin ekvivalentidir,əsaslandırma həm nisbi, həm də müqayisə olunmamış parçalar üçün doğru olaraq qalsa da,Dekartın özü sonuncunu "kar ədədlər" (nombres sourds) adlandırdı. Nyuton mühazirələrində də ədədləri üç növə bölür: tam ədədlər (vahidlə ölçülür), kəsr (vahidin çoxlu kəsrləri) və irrasional ədədlər (bölmə ilə ölçülməz). 1710-cu ildən bəri sayın belə bir tərifi bütün dərsliklərə qəti şəkildə daxil edilmişdir..

 

Hesab cədvəlləri. 1835-ci il

Dövrü kəsrlər 1603-cü ildə İ.Q. Beyerin "Onluq Hesab" (Logistica decimalis) əsərində meydana çıxmışdır. Con Vallis 1685-ci ildə "Cəbr haqqında traktatında" bunların üzərində işləməyi davam etdirdi və burada azalmayan ${\displaystyle p/q}$  kəsr üçün bir dövrün rəqəmlərinin ${\displaystyle q-1}$ -dən az və ya bərabər olduğunu müəyyən etdi. Bundan əlavə, Vallis, ${\displaystyle 2^{m}5^{n}}$  formasının məxrəci ilə kəsrlərin sonluğunu göstərdi, eyni zamanda dövrü kəsrlərlə irrasional ədədləri ifadə etməyin mümkün olmadığını da bildirdi.

XVII əsrin əvvəllərində Con Neper loqarifmik xətkeş və loqarifmanı icad etdi. Loqarifmaların və onluq kəsrlərin istifadəsi, rasional yaxınlaşmalar ardıcıllığı kimi irrasional ədədlər anlayışının hesaba daxil edilməsi XVII əsrin sonlarında hesabın əhatə dairəsini genişləndirdi və davamlı kəmiyyətlərin öyrənilməsi üçün elmin əsas əhəmiyyətini müəyyənləşdirdi.

XVIII əsrdə onluq kəsrlər,xüsusən sonsuz və dövrü onluq kəsrlər üzərində iş davam etdi.Hər hansı bir dövriü kəsrin rasional bir sıra olması və məxrəcdə iki və beşdən başqa sadə bölücü olan hər hansı bir azalmayan kəsrin dövrü olaraq parçalanması,riyaziyyatda π (pi) ədədinin irrasional olması,XVIII əsrin ortalarında İohann Lambert tərəfindən sübut edildi. Karl Fridrix Qauss "Ədədi tədqiqatlar" əsərində kvadratik çıxıq nəzəriyyəsi, kvadratik formaların qısa ifadəsi, n-dərəcəli tənliklər nəzəriyyəsi öz əksini tapmışdır,bu nəzəriyyədən istifadə edərək dövrü kəsrlərin daha dərin xüsusiyyətlərini təqdim edir. Eyni zamanda, o dövrün dərsliklərində, onluq kəsrlərə keçərkən üzdən toxunulur və ya ümumiyyətlə qeyd olunmurdu. Leonard Eyler davamlı kəsrlərlə məşğul idi, ilk dəfə sonsuz davam edən kəsrləri sonsuz seriyaya çevirmə üsullarını təqdim etdi; sonra 1748-ci ildə "Analizə giriş"in,birinci cildində onlara bir fəsil həsr etmişdir. Eyler, hər rasional ədədin sonlu davam edən bir kəsr kimi göstərilə biləcəyinə və rəqəmlərdə vahidləri olan dövrü fasiləsiz kəsrin kvadrat tənliyin kökü olduğuna dair dəlillərə sahibdir. Bunun əksini 1768-ci ildə Jozef Lui Laqranj sübut etdi. XVIII əsrdə Eyler və onun tələbələri hesabı müasir formaya gətirdilər.

Alber Jirar və Dekart mənfi ədədləri həndəsi olaraq əks istiqamətli parçalar şərh etdilər. Baxmayaraq ki, Dekart müsbət, həqiqi köklərlə yanaşı bərabərliklərin mənfi köklərini də artıq hesab etmişdir(xəyali fərqli olaraq),mənfi ədədlərin bəzi xassələri uzun müddət bəlli deyildi. 1742-ci il sentyabrın 1-də Leonard Eyler Nikolay I Bernoulliyə göndərdiyi məktubda əvvəlcə hər hansı bir cəbri tənliyin köklərinin ${\displaystyle a+b{\sqrt {-1}}}$  forma alması barədə məlumat verdi. 1747-ci ildə "Küləklərin ümumi səbəbi haqqında düşüncələrində" Dalember ${\displaystyle (a+b{\sqrt {-1}})^{g+h{\sqrt {-1}}}=A+B{\sqrt {-1}}}$  göstərdi. "Xəyali köklər üzərində aparılan araşdırmalarında" Eyler xəyali bir rəqəmi "sıfırdan böyük və ya sıfırdan az, sıfıra bərabər olmayan", lakin "mümkün olmayan bir şey" olaraq təyin edir. Üstəlik, hər bir xəyali nömrənin ${\displaystyle M}$  həqiqi sayının və həqiqi ${\displaystyle N}$ -nin ${\displaystyle {\sqrt {-1}}}$  əmsalı ilə əmələ gəldiyi teoremini sübut edir. Problem fərdi funksiyalar üçün həll edildi, xəyali ədədlərə edilən əməliyyatların dairəsi açıqlanmadı. Bundan əlavə,xəyali ədədlərin həndəsi şərhlərində də problemlər var. İlk cəhd xəyali ədədlərin gerçəyə perpendikulyar olan parçalar olduğuna inanan Vallis tərəfindən edildi, sonra 1753-cü ildə Henrix Kyun əsərində,xəyali bir ədədi mənfi sahəsi olan bir kvadratın tərəfi hesab edirdi. Kaspar Vessel və Jan Roben Arqan, Vallis tərifini yalnız XVIII-XIX əsrin sonlarında inkişaf etdirməyə müvəffəq oldular.

Say nəzəriyyəsinin yaranması və inkişafı

XVII əsrin 30-cu illərində Pyer Ferma yalnız Evkliddən və bəlkə də Diofantdan təsirlənirək say nəzəriyyəsini hesab sahəsi olaraq ayırdı. Pyer Ferma Diofant tənliklərinin və tam ədədlərin bölünməsinin həllində iştirak edirdi. O, sübutu olmadan bir sıra teoremlər hazırladı, xüsusən də Kiçik və Böyük Ferma teoremlərini. Pyer Ferma say nəzəriyyəsinə dair xüsusi bir əsər yazmadı,onun təklifləri yalnız yazışmalarda, həm də Diofantın "Arifmetikası"nda şərh şəklində qorunurdu.

70 ildən sonra Fermanın işi bir neçə onilliklər boyu say nəzəriyyəsi ilə məşğul olan Leonard Eylerin diqqətini çəkdi. Eyler 30 cildlik riyazi seriyasının dörd yarım tomunu ona həsr etmişdir. Eyler kiçik Ferma teoremini ümumiləşdirdi,eyni zamanda 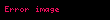${\displaystyle n=3}$  böyük Ferma teoreminin sübutudur. Eyler ilk olaraq riyaziyyatın digər sahələrinin aparatlarından say nəzəriyyəsi problemləri, ilk növbədə riyazi analiz üçün istifadə etdi. O,funksiyaları yaradan metodu,rieman zeta funksiyasını,sadə ədədlərin toplanması ilə bağlı problemləri ümumiləşdirdi.

Eylerin işindən sonra say nəzəriyyəsinin ayrıca bir elmə çevrildiyi güman edilir.

Hesablamanın əsaslandırılması problemləri

 

Cüzeppe Peano

XIX əsrdə baş verən riyaziyyat əsaslarının tənqidi nəzərdən keçirilməsi prosesi,Nikolay Lobaçevskinin həndəsə işi ilə bağlıdır. Hələ XVIII əsrdə ədədlər üçün nəzəri əsaslandırmalar verməyə başladı. Əvvəlcə bu yalnız Evklid prinsiplərindən götürülən müxtəlif aksiom və təriflərin tətbiq olunduğu, çox vaxt lazımsız və eyni zamanda yetərsiz olan natural ədədlərin hesablanmasına aiddir. Hesabın əsas qanunları da belə idi: komutativ və vurma,toplama qanunları çox tez-tez xatırlandığı assosiativ,paylama qanunu toplama və vurmaya nisbətən - daha azdır və bütün bu beş qanun son dərəcə nadirdir. Qotfrid Leybnits öncə arifmetikanın deduktiv qurulması vəzifəsini qoymuş və xüsusilə, 1705-ci ildə etdiyi "İnsanın ağılındakı yeni təcrübələr" əsərində "iki üstə gəl iki bərabərdir dörd" bərabərliyini sübut etməyin zəruriliyini göstərmişdi. Bu məsələni həll etmək üçün 1770-ci ildə Xristian Volf, 1790-cı ildə Şultz, 1822-ci ildə Martin Om, 1861-ci ildə Qerman Qrassman və nəhayət 1889-cu ildə Cüzeppe Peano öz aksiomlarını təqdim etdi.

Arifmetikanın əsas prinsiplərini vurğulamağın çətinliyi onun ilkin mövqelərinin sadəliyi ilə əlaqədardır. Yalnız XIX əsrin ortalarında Qrassman toplama və vurmanı müəyyən edən əsas aksiomlar sistemini seçdi. Sistem hesabın qalan mövqelərini aksiomların məntiqi nəticəsi kimi əldə etməyə imkan verdi. Əsas aksiomlar əsasında toplama və vurma dəyişikliyinin komutativ, assosiativ və paylayıcı qanunları sübut edildi,kəsr anlayışını müəyyən müqayisə və hərəkət qanunları ilə cüt tam ədəd kimi təqdim olunur. Qrassmanın işi Peano tərəfindən davam etdirildi. Kurt Hödel 1932-ci ildə natamamlıq teoremini sübut edənə qədərnatural ədədlərin hesablanmasının tam nəzəri əsaslandırılmasına, xüsusən David Hilbertin əsərinə yaxınlaşmaq üçün daha çox cəhdlər edildi.

Eynilə,iki konsepsiya: vahidin bərabər kəsrləri və ya iki vahid dəyərin nisbəti önə çıxan rasional kəsrlər üçün nəzəri əsaslandırma cəhdləri oldu. Rasional kəsrlər üçün əlavə olaraq kəsrlərin toplanması və çıxılmasında istifadə olunan bərabərliyi ${\displaystyle {\frac {am}{bm}}={\frac {a}{b}}}$  и ${\displaystyle {\frac {a:m}{b:m}}={\frac {a}{b}}}$  (${\displaystyle m}$  — natural ədəd) sübut etmək lazım idi. Bərabərlik münasibət nəzəriyyəsində mənasız idi, lakin müstəqil olmayan bir konsepsiyada heç də aydın deyildi. Lakin o, sadəcə sadiq sayılırdı. Kəsrlərin arifmetikliyi 1894-cü ildə J. Tanneri tərəfindən əsaslandırılmışdır,onun modelində kəsrlər cüt ədəd kimi göstərilmişdir.

1758-ci ildə "Hesabın, həndəsənin, planetin və sferik triqonometriyanın inkişafının ilk əsaslarında" Kestner bütün hesab anlayışların tam bir say ilə əsaslandırılmasını müdafiə etdi. Beləliklə, kitab qaydası ilə natural ədədləri, kəsrləri, mənfi ədədləri, onluq kəsrləri, irrasional ədədləri və yalnız bundan sonra əlaqələr nəzəriyyəsini təyin etdi. İrrasional ədədlər üzərində əməliyyatlar,rasional kəsrlərin yaxınlaşmalarına əsaslanaraq araşdırılmağa başladı. Üstəlik, irrasional ədədlərin mövcudluğu əvvəlcədən qəbul edildi və özləri də rasional ədədlərin ardıcıllığının hüdudları kimi şərh edildi. İrrasional ədədlər üçün Nyutonun tərifi,nisbi kəmiyyətlərin əlaqələri kimi istifadə edildi (Leonard Eyler buna bənzər bir tərif verdi). P.A.Rəhmanov "Həndəsi cəhətdən müqayisə olunan və qeyri-mütənasib miqdarın məzmunu və nisbətlərinin yeni bir nəzəriyyəsi və sonuncu vəziyyətdə həddlər nəzəriyyəsində" irrasional ədədlərə eyni şəkildə münasibət göstərdi. Yalnız XIX əsrin ikinci yarısında Şarl Mere, Georq Kantor, Riçard Dedekind və Karl Vilhelm Veyerştrass tərəfindən tərtib edilmiş həqiqi ədədlərin ciddi nəzəriyyələri meydana çıxdı.

Mənfi ədədlər nəzəriyyəsinin formalaşmasında əsas problem mənfi ədədin sıfırdan az olması, yəni heç bir şeydən az olmasıdır. İşarələr üçün qaydalar tərtib etməyə cəhd edilərkən mənfi ədədlərin ciddi tərifi yox idi("minus üstəgəl plus mənfi verir" və "minus üstəgəl mənfi plus verir"). 1813-cü ildə bir fransız riyaziyyatçısı Lazar Carno yazırdı: "İşarələrin qayda-qanunlarının metafizikası daha dərindən araşdırılsa, bəlkə də daha böyük ,sonsuz kəmiyyətlərin metafizikasından daha çox çətinlikləri ortaya qoyur; bu qayda heç vaxt tamamilə qənaətbəxş şəkildə sübut edilməmişdir və görünür,hətta kafi bir şəkildə sübut edilə bilməz". Mənfi ədədlər nəzəriyyəsini formalaşdırmaq üçün ilk cəhdlər XIX əsrin ortalarında edilmiş, Uilyam Rouen Hamilton və Qrassmana aiddir.

Kompleks ədədlərin tam həndəsi təsviri Kaspar Vessel tərəfindən 1799-cu ildə "İstiqamət və analitik təmsilçilik təcrübəsi, əsasən də müstəvi və sferik çoxbucaqlıların həllində" əsərində təklif edilmişdir. Vessel,cəbr əməliyyatlarından istifadə edərək təyyarədə yön parçaları ilə işləmək istədi,ancaq həqiqi ədədlər üçün,yalnız istiqaməti əks istiqamətə dəyişməyə və özbaşına bir istiqamət qurmamağa icazə verdilər.Vessel əsas vahidlərdən ${\displaystyle +1}$ , ${\displaystyle -1}$ , ${\displaystyle +\epsilon }$ , ${\displaystyle -\epsilon }$  istifadə etdi və vurma əməlindən istifadə edərək ${\displaystyle \epsilon ={\sqrt {-1}}}$  nəticəsinə gəldi. Vesselin əməyi təqribən 100 il ərzində diqqətdən kənarda qaldı. Bu müddət ərzində Jan Rober Arqan, 1813-1814-cü illərdə xəyali ədədlərin şərhini verdi, 1831-ci ildə Şayss "Bikvadrat qalıqlar nəzəriyyəsini, həmçinin 1832-ci ildə Hamilton,kompleks ədədləri həqiqi cüt kimi qəbul edən hesab nəzəriyyəsini qurdu.

Vessel ünəzəriyyəni,üçölçülü boşluqda ümumiləşdirməyə çalışdı,amma bacarmadı.Uilyam Rouen Hamilton,vurulduqda kvaternion qanunu ödəməyən qraflar nəzəriyyəsini qurana qədər sual açıq formada qaldı. Ancaq Karl Vilhelm Veyerştrass, Ferdinand Frobenius və Benjamin Pirsin araşdırmaları göstərdi ki,kompleks ədədlərdən kənarda ədədlər anlayışının genişlənməsi ilə hər hansı bir hesab qanunundan imtina edilməlidir.

Azərbaycanda riyaziyyatın tərəqqisi

Orta əsrlərdə İslam dünyasında riyaziyyat yüksək inkişaf dərəcəsinə çatmışdı. Evklid həndəsəsi və qeyri-Evklid həndəsəsinə yol açan paralellik postulatı, triqonometriya, cəbri tənliklərin (xüsusilə kvadrat və kub tənliklərin) həlli, sferik həndəsə və riyaziyyatın astronomiyaya tətbiqi, onluq kəsrlərin kəşfi, funksiya və limit anlayışlarının inkişafı Yaxın Şərqdə vüsət tapmışdı. Marağa rəsədxanasının təşkilatçısı və rəhbəri Mühəmməd ibn Həsən Nəsirəddin Tusi (1201-1274) elm aləmində tək öz zəmanəsinin deyil, bütün dövrlərin ən böyük riyaziyyatçı və astronomlarından biri olaraq qəbul edilmişdir.

14-cü əsrdən başlayaraq İslam dünyasında, o cümlədən Azərbaycanda riyaziyyat sahəsində kəşf və tədqiqatlar zəiflədi. 16-cı əsrdə Avropa riyaziyyatçıları və astronomları ön sıraya çıxdılar.

Yüksək ixtisaslı riyaziyyatçıların yetişməsi Azərbaycanda yalnız sövet dövrünün 30-cu illərində özünü göstərməyə başladı. Mikayıl Xıdırzadə, İbrahim İbrahimov, Zahid Xəlilov, Əşrəf Hüseynov rus riyaziyyat məktəbinin yetişdirdiyi ilk riyaziyyatçılar oldular. 50-ci illərdə Azərbaycan riyaziyyatçıları kəmiyyət və keyfiyyətcə artmağa başladılar. 70-ci illərdən başlayaraq Azərbaycanda riyaziyyatın geniş vüsət tapdığı, riyazi mədəniyyətin inkişaf etdiyi bir dövr hesab olunur.

Məcid Rəsulov, Məqsud Cavadov, Qoşqar Əhmədov, Cəlal Allahverdiyev, Mirabbas Qasımov, Arif Babayev, Sasun Yaqubov, Hamlet İsayev, Abbas Əzimov, , Fərhad Hüseynov, Hüseyn Hüseynov, Arif Səlimov, Oqtay Vəliyev, Rəşid Məmmədov və başqa Azərbaycan riyaziyyatçıları Sovet İttifaqında və Qərbdə qiymətləndirilən elmi nəticələr aldılar.

İstinadlar

1. Boyer & Merzbach, 2010, Concepts and Relationships
2. Arithmetic
3. История математики, т. I, 1970. səh. 9—12
4. Депман, 1965. səh. 18—20
5. Mallory, J. P. (1997). Encyclopedia of Indo-European Culture / J. P. Mallory, Q. A. Douglas. L.: Fitzroy Dearborn Publishers. ISBN 9781884964985..
6. Мах Э. (1979). "Познание и заблуждение". Альберт Эйнштейн и теория гравитации. М.: Мир. 74 (подстрочное примечание).: «прежде чем возникнет понятие о числе, должен существовать опыт, что в известном смысле равноценные объекты существуют множественно и неизменно».
7. История математики, т. I, 1970. səh. 12—13
8. Арнольд, 1970
9. Фролов, Б. А (1974). Числа в графике палеолита. Новосибирск: Наука. səh. 93—94.
10. Арифметика, 1951. səh. 12—13
11. Арифметика, 1951. səh. 24
12. Беллюстин, 1909, Глава 4: Различные системы счисления
13. Меннингер, 2011. səh. 100
14. История математики, т. I, 1970. səh. 19—20
15. Scott, 1958. səh. 8
16. Депман, 1965. səh. 49—52
17. История математики, т. I, 1970. səh. 21
18. История математики, т. I, 1970. səh. 23—24
19. История математики, т. I, 1970. səh. 25
20. История математики, т. I, 1970. səh. 34
21. История математики, т. I, 1970. səh. 35
22. История математики, т. I, 1970. səh. 37—39
23. Scott, 1958. səh. 10
24. История математики, т. I, 1970. səh. 36
25. История математики, т. I, 1970. səh. 40
26. История математики, т. I, 1970. səh. 50
27. История математики, т. I, 1970
28. Scott, 1958. səh. 40—41
29. История математики, т. I, 1970. səh. 62
30. История математики, т. I, 1970. səh. 64
31. Депман, 1965. səh. 53—54
32. История математики, т. I, 1970. səh. 67
33. История математики, т. I, 1970. səh. 68
34. История математики, т. I, 1970. səh. 68—69
35. Scott, 1958. səh. 20
36. История математики, т. I, 1970. səh. 70—72
37. История математики, т. I, 1970. səh. 73
38. История математики, т. I, 1970. səh. 94—98
39. История математики, т. II, 1970. səh. 33—35
40. История математики, т. I, 1970. səh. 106
41. История математики, т. I, 1970. səh. 111—114
42. История математики, т. I, 1970. səh. 128
43. Выгодский, 1967. səh. 265
44. История математики, т. I, 1970. səh. 139
45. История математики, т. I, 1970. səh. 143
46. История математики, т. I, 1970. səh. 144—146
47. История математики, т. I, 1970. səh. 146—148
48. Депман, 1965. səh. 57—58
49. История математики, т. I, 1970. səh. 178
50. История математики, т. I, 1970. səh. 157—160
51. История математики, т. I, 1970. səh. 162—163
52. История математики, т. I, 1970. səh. 167—169
53. Депман, 1965. səh. 62—68
54. История математики, т. I, 1970. səh. 181—183
55. История математики, т. I, 1970. səh. 201
56. История математики, т. I, 1970. səh. 194—195
57. История математики, т. I, 1970. səh. 205—209
58. История математики, т. I, 1970. səh. 209—210
59. Депман, 1965. səh. 90—94
60. Депман, 1965
61. История математики, т. I, 1970. səh. 212—214
62. История математики, т. I, 1970. səh. 216—218
63. История математики, т. I, 1970. səh. 218—219
64. История математики, т. I, 1970. səh. 227—229
65. История математики, т. I, 1970. səh. 249—250
66. Меннингер, 2011. səh. 80—81
67. Меннингер, 2011. səh. 83—84
68. Ifrah, 2000. səh. 310
69. Boyer & Merzbach, 2010, Early Number Bases
70. Депман, 1965. səh. 61
71. Депман, 1965. səh. 59
72. Ifrah, 2000. səh. 322
73. История математики, т. I, 1970. səh. 254—256
74. Арифметика, 1951
75. История математики, т. I, 1970. səh. 261—265
76. История математики, т. I, 1970. səh. 289—290
77. История математики, т. I, 1970. səh. 286—287
78. История математики, т. I, 1970. səh. 304—306
79. История математики, т. I, 1970. səh. 316
80. История математики, т. I, 1970. səh. 307
81. История математики, т. II, 1970. səh. 34—36
82. История математики, т. III, 1972. səh. 45—47
83. История математики, т. II, 1970. səh. 36—39
84. А. П. Юшкевич (1972). История математики. III. М.: Наука. səh. 61-66.
85. А. П. Юшкевич (1972). История математики. III. М.: Наука. səh. 61-66.
86. История математики, т. II, 1970. səh. 74
87. История математики, т. II, 1970. səh. 78
88. История математики, т. II, 1970
89. История математики, т. III, 1972. səh. 37—38
90. А. А. Карацуба, Чаган — Экс-ле-Бен (1978). Чисел теория. 29. M: Советская энциклопедия,.
91. История математики, т. II, 1970. səh. 17
92. История математики, т. III, 1972. səh. 47—49
93. История математики, т. III, 1972. səh. 49—52
94. А. П. Юшкевич (1972). История математики. III. М.: Наука. səh. 61-66.
95. История математики, т. III, 1972
96. А. П. Юшкевич (1972). История математики. III. М.: Наука. səh. 61-66.
97. А. П. Юшкевич (1972). История математики. III. М.: Наука. səh. 61-66.
98. http://www.anl.az/el/a/Azf-265604.pdf
99. http://anl.az/down/meqale/kitabxanashunasliq-biblioqrafiya/1_2009/ka.pdf

Ədəbiyyat

• Беллюстин, В. (1909). Как_постепенно_дошли_люди_до_настоящей_арифметики Как постепенно дошли люди до настоящей арифметики (#bad_url). М.: Типография К. Л. Меньшова.
• Выгодский, М. Я. (1967). Арифметика и алгебра в древнем мире. М.: Наука.
• Депман, И. Я. (1965). История арифметики. М.: Просвещени.
• Матвиевская Г. П. (1967). Учение о числе на средневековом Ближнем и Среднем Востоке. Ташкент: ФАН. Вопреки названию, книга прослеживает историю чисел и арифметики с самых древних времён.
• Меннингер, К. (2011). История цифр. Числа, символы, слова. М.: ЗАО Центрполиграф. ISBN 9785952449787.
• Boyer, C. B. (2010). A History of Mathematics. John Wiley & Sons.
• Ifrah, G. (2000). The Universal History of Numbers. John Wiley & Sons. ISBN 0471393401.
• Scott, J. F. (1958). A History of Mathematics From Antiquity to the Beginning of the Nineteen Century. L.: Tailor & Francis Ltd.
• 2 (1890—1907). "Арифметика" . Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). СПб..
• История математики. I. М.: Наука. под ред. А. П. Юшкевича. 1970.
• История математики. II. М.: Наука. под ред. А. П. Юшкевича. 1970.
• История математики. III. М.: Наука. под ред. А. П. Юшкевича. 1972.
• Энциклопедия элементарной математики. М.: Государственное издательство технико-теоретической литературы. под ред. Александров, Павел Сергеевич, А. И. Маркушевича и А. Я. Хинчина. 1951.

Həmçinin bax

Sitat səhvi: <ref> tags exist for a group named "qeyd.", but no corresponding <references group="qeyd."/> tag was found