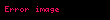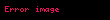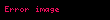Hörner sxemi (və ya Hörner üsulu) qismət çoxhədlisinin tapılması alqoritmi. Qalıqlı bölmənin tərifinə görə n dərəcəli
çoxhədlisini, x-α ikihədlisinə böldükdə qismət çoxhədlisi n-1 dərəcəli çoxhədli qalıq isə ədəd olur.
qismət çoxhədlisinin əmsallarını və qalığı Hörner sxemi adlanan xüsusi üsulun köməyi ilə asan tapmaq olur.
İzahı
Tərifə görə
bərabərliyinin sağ tərəfində mötərizələri açıb, onu x-in dərəcələrinə görə düzsək, iki çoxhədli bərabərlik şərtinə əsasən yaza bilərik ki,
Buradan, 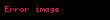
şəklində taparıq. Göründüyü kimi bölünən çoxhədlinin əmsalları və α məlum olduqda qismət çoxhədlisinin əmsallarını və r-ə qiymətlər verməklə asanlıqla (2) düsturlarından təyin etmək olar.
Qismət çoxhədlisinin bu üsulla tapılmasına Hörner sxemi deyilir və adətən, bu sxem cədvəl şəklində verilir. Bu cədvəlin birinci sətrində P(x)-in əmsalları, ikinci sətrində isə ardıcıl olaraq, bölmənin sərbəst həddi Q(x)-in əmsalları və qalıq yazılır.
| an | an-1 | ... | a1 | a0 | |
| α | bn-1=a | bn-2=αbn-1+an-1 | b0=αb1+a1 | r=αb0+a0 |
Nümunə:
çoxhədlisini x+2 ikihədlisinə bölək. Bunun üçün Hörner sxemini tətbiq edək.
| 1 | 0 | -2 | 0 | 4 | -7 | |
| -2 | 1 | -2 | 2 | -4 | 12 | -31 |
Deməli, 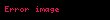
Mənbə
- Cəbr və analizin başlanğıcı - Ümumtəhsil məktəblərinin XI sinfi üçün dərslik; M.C.Mərdanov, M.H.Yaqubov, S.S.Mirzəyev, A.B.İbrahimov, İ.H.Hüseynov, M.A.Kərimov, Ə.F.Quliyev; Çaşıoğlu nəş. 2007-ci il.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Horner sxemi ve ya Horner usulu qismet coxhedlisinin tapilmasi alqoritmi Qaliqli bolmenin terifine gore n dereceli P x anxn an 1xn 1 a1 a0 displaystyle P x a n x n a n 1 x n 1 a 1 a 0 coxhedlisini x a ikihedlisine boldukde qismet coxhedlisi n 1 dereceli coxhedli qaliq ise eded olur Q x bn 1xn 1 bn 2xn 2 b1 b0 displaystyle Q x b n 1 x n 1 b n 2 x n 2 b 1 b 0 qismet coxhedlisinin emsallarini ve qaligi Horner sxemi adlanan xususi usulun komeyi ile asan tapmaq olur IzahiTerife gore anxn an 1xn 1 a1 a0 x a bn 1xn 1 bn 2xn 2 b1 b0 r displaystyle a n x n a n 1 x n 1 a 1 a 0 x alpha b n 1 x n 1 b n 2 x n 2 b 1 b 0 r beraberliyinin sag terefinde moterizeleri acib onu x in derecelerine gore duzsek iki coxhedli beraberlik sertine esasen yaza bilerik ki an bn 1 displaystyle a n b n 1 an 1 bn 2 abn 1 displaystyle a n 1 b n 2 alpha b n 1 an 2 bn 3 abn 2 displaystyle a n 2 b n 3 alpha b n 2 displaystyle displaystyle a3 b2 ab3 displaystyle a 3 b 2 alpha b 3 a2 b1 ab2 displaystyle a 2 b 1 alpha b 2 a1 b0 ab1 displaystyle a 1 b 0 alpha b 1 a0 r ab0 displaystyle a 0 r alpha b 0 Buradan Q x bn 1xn 1 bn 2xn 2 b1 b0 displaystyle Q x b n 1 x n 1 b n 2 x n 2 b 1 b 0 qismet emsallarini ve r qaligini bn 1 an displaystyle b n 1 a n bn 2 an 1 abn 1 displaystyle b n 2 a n 1 alpha b n 1 bn 3 an 2 abn 2 displaystyle b n 3 a n 2 alpha b n 2 displaystyle 2 displaystyle 2 b2 a3 ab3 displaystyle b 2 a 3 alpha b 3 b1 a2 ab2 displaystyle b 1 a 2 alpha b 2 b0 a1 ab1 displaystyle b 0 a 1 alpha b 1 r a0 ab0 displaystyle r a 0 alpha b 0 seklinde tapariq Gorunduyu kimi bolunen coxhedlinin emsallari ve a melum olduqda qismet coxhedlisinin emsallarini ve r e qiymetler vermekle asanliqla 2 dusturlarindan teyin etmek olar Qismet coxhedlisinin bu usulla tapilmasina Horner sxemi deyilir ve adeten bu sxem cedvel seklinde verilir Bu cedvelin birinci setrinde P x in emsallari ikinci setrinde ise ardicil olaraq bolmenin serbest heddi Q x in emsallari ve qaliq yazilir an an 1 a1 a0a bn 1 a bn 2 abn 1 an 1 b0 ab1 a1 r ab0 a0 Numune x5 23 4x 7 displaystyle x 5 2 3 4x 7 coxhedlisini x 2 ikihedlisine bolek Bunun ucun Horner sxemini tetbiq edek 1 0 2 0 4 7 2 1 2 2 4 12 31 Demeli Q x x4 2x3 2x2 4x 12 displaystyle Q x x 4 2x 3 2x 2 4x 12 R 31 MenbeCebr ve analizin baslangici Umumtehsil mekteblerinin XI sinfi ucun derslik M C Merdanov M H Yaqubov S S Mirzeyev A B Ibrahimov I H Huseynov M A Kerimov E F Quliyev Casioglu nes 2007 ci il
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State