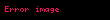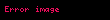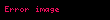Kompleks ədədlər (lat. complex) - şəklində olan ifadəyə deyilir.

Tarixi
"Kompleks ədədlər" terminini ilk dəfə fransız alimi işlətmişdir. Kompleks ədədlərinin həndəsi izahını isə Norveç əsilli Danimarka alimi vermişdir. Xəyali ədədin simvolu ("i") 1777-ci ildə isveçrə alimi Leonard Eyler tərəfindən işlədilmişdi. Sözün kökü olan "imaginarius" ifadəsi latınca "xəyali" deməkdir.
Xarakteristika
Kvadrat tənliklərində diskriminant sıfırdan kiçikdirsə, onda bu tənliyin həqiqi ədədlər çoxluğunda kökü yoxdur. Məs. x2+9=0 tənliyinin həqiqi ədədlər çoxluğunda kökü yoxdur. Buradan alınır ki, həqiqi ədədlər çoxluğunu elə genişləndirmək lazımdır ki, yeni tənliyin kökü olsun, vurma və toplama əməllərinin xassələri saxlanılsın. Bu məqsədlə (xəyali vahid) daxil edilir. "i" ədədi daxil edildikdən sonra çoxluğu elə genişləndirmək lazımdır ki, bütün həqiqi ədədlər və "i" ədədi bu çoxluğa daxil olsun. a və b ədədləri isə həqiqi ədədlər olduğundan bi hasili daxil edək. Buradan alınır: a + bi.
z = a+bi şəklində olan ifadə və ya i2 = -1 şərtini ödəyən i ədədinə Kompleks ədəd deyilir. Burada a-ya z-in həqiqi hissəsi deyilir və Re(z) = a düsturu şəklində, b-yə isə z-in xəyali hissəsi deylir və Im(z)= b düsturu şəklində yazılır. Buradan alınır ki, həqiqi ədədlər kompleks ədədlərinin içərisindədir. Aşağıda kompleks ədələrinin növləri göstərilmişdir:
- Cəbri şəkildə verilmiş kompleks ədədlər: z = a+bi şəklində olan kompleks ədədə deyilir.
- Tərs kompleks ədədlər: hasili 1-ə bərabər olan kompleks ədədə deyilir: zw=1.
- Kompleks ədədlərin bərabərliyi:əgər iki kompleks ədəd bərabərdirsə, onların xəyali və həqiqi hissələri də bir-brinə bərabərdir: z=w , a=b.
- Sırf : 0 + bi şəklində olan ifadəyə deyilir. 0 ədədi yeganə kompleks ədəddir ki, həm sırf xəyali , həm də .
Kompleks ədədlərinin triqonometrik forması
Verilmiş kompleks ifadəni triqonometrik şəklə gətirmək üçün aşağıdakı üsullardan istifadə edilir:
- |z| = R2 = a2 + b2 (məsələn; 2 – 3i olduqda, a=2 və b= -3)
- cos α = a / R , sin α = b / R.
- z = R (cos α + isin α)
Verilən cos α = a / R və sin α = b / R ifadələrində arqument olan α bucağını hesablamaq üçün aşağıdakı üsullardan istifadə edilir:
- 1) + sin α və – cos α olduqda, tapılan bucaq π-dən çıxılır.(2-ci rüb)
- 2) – sin α və – cos α olduqda, tapılan bucaq π üzərinə əlavə edilir.(3-cü rüb)
- 3) – sin α və + cos α olduqda, tapılan bucaq 2π-dən çıxılır.(4-cü rüb)
- 4) + sin α və + cos α olduqda, tapılan bucaq olduğu kimi qalır.(1-ci rüb)
Formullar
- Fərqləndirmə:
ifadəsi,
və
bərabərliklərini bildirir.
- Toplama:
- Çıxılma:
- Vurma:
- Bölmə:
Kompleks ədədlərə aid misallar
- Toplama:
- Çıxılma:
- Vurma:
1➕i
- Modul:
Resurs
Riyazi istinadları
- Conway, John B. Functions of One Complex Variable I. Springer. 1986. ISBN .
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP. Section 5.5 Complex Arithmetic // Numerical Recipes: The Art of Scientific Computing (3rd). New York: Cambridge University Press. 2007. ISBN .
Tarixi istinadları
- Nahin, Paul J. An Imaginary Tale: The Story of
(hardcover). Princeton University Press. 1998. ISBN .
- A gentle introduction to the history of complex numbers and the beginnings of complex analysis.
- H.-D. Ebbinghaus ... Numbers (hardcover). Springer. 1991. ISBN .
- An advanced perspective on the historical development of the concept of number.
Xarici keçidlər

- at Convergence. MAA Mathematical Sciences Digital Library.
- John and Betty's Journey Through Complex Numbers
- Dimensions: a math film.
- Wikibooks: Komplexe Zahlen
- Geschichte der komplexen Zahlen
- Eine Facharbeit, die eine Einführung in die komplexen Zahlen gibt
- Rechnen mit komplexen Zahlen
- Dimensions: a math film. Einbettung der komplexen Zahlen in die Darstellung höherer Dimensionen (auch Chaostheorie) insb. Kapitel 5 und 6
- Java-Applet zur geometrischen Deutung 2013-04-13 at the Wayback Machine
- Java-Klasse, zur Berechnung komplexer Zahlen
- Rechner für komplexe Zahlen
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Kompleks ededler lat complex z a bi displaystyle z a bi seklinde olan ifadeye deyilir Kompleks ededlerinin hendesi formasiTarixi Kompleks ededler terminini ilk defe fransiz alimi isletmisdir Kompleks ededlerinin hendesi izahini ise Norvec esilli Danimarka alimi vermisdir Xeyali ededin simvolu i 1777 ci ilde isvecre alimi Leonard Eyler terefinden isledilmisdi Sozun koku olan imaginarius ifadesi latinca xeyali demekdir XarakteristikaKvadrat tenliklerinde diskriminant sifirdan kicikdirse onda bu tenliyin heqiqi ededler coxlugunda koku yoxdur Mes x2 9 0 tenliyinin heqiqi ededler coxlugunda koku yoxdur Buradan alinir ki heqiqi ededler coxlugunu ele genislendirmek lazimdir ki yeni tenliyin koku olsun vurma ve toplama emellerinin xasseleri saxlanilsin Bu meqsedle I ededi xeyali vahid daxil edilir i ededi daxil edildikden sonra coxlugu ele genislendirmek lazimdir ki butun heqiqi ededler ve i ededi bu coxluga daxil olsun a ve b ededleri ise heqiqi ededler oldugundan bi hasili daxil edek Buradan alinir a bi z a bi seklinde olan ifade ve ya i2 1 sertini odeyen i ededine Kompleks eded deyilir Burada a ya z in heqiqi hissesi deyilir ve Re z a dusturu seklinde b ye ise z in xeyali hissesi deylir ve Im z b dusturu seklinde yazilir Buradan alinir ki heqiqi ededler kompleks ededlerinin icerisindedir Asagida kompleks edelerinin novleri gosterilmisdir Cebri sekilde verilmis kompleks ededler z a bi seklinde olan kompleks edede deyilir Ters kompleks ededler hasili 1 e beraber olan kompleks edede deyilir zw 1 Kompleks ededlerin beraberliyi eger iki kompleks eded beraberdirse onlarin xeyali ve heqiqi hisseleri de bir brine beraberdir z w a b Sirf 0 bi seklinde olan ifadeye deyilir 0 ededi yegane kompleks ededdir ki hem sirf xeyali hem de Kompleks ededlerinin triqonometrik formasiVerilmis kompleks ifadeni triqonometrik sekle getirmek ucun asagidaki usullardan istifade edilir z R2 a2 b2 meselen 2 3i olduqda a 2 ve b 3 cos a a R sin a b R z R cos a isin a Verilen cos a a R ve sin a b R ifadelerinde arqument olan a bucagini hesablamaq ucun asagidaki usullardan istifade edilir 1 sin a ve cos a olduqda tapilan bucaq p den cixilir 2 ci rub 2 sin a ve cos a olduqda tapilan bucaq p uzerine elave edilir 3 cu rub 3 sin a ve cos a olduqda tapilan bucaq 2p den cixilir 4 cu rub 4 sin a ve cos a olduqda tapilan bucaq oldugu kimi qalir 1 ci rub FormullarFerqlendirme a bi c di displaystyle a bi c di ifadesi a c displaystyle a c ve b d displaystyle b d beraberliklerini bildirir Toplama a bi c di a c b d i displaystyle a bi c di a c b d i Cixilma a bi c di a c b d i displaystyle a bi c di a c b d i Vurma a bi c di ac bci adi bdi2 ac bd bc ad i displaystyle a bi cdot c di ac bci adi bdi 2 ac bd bc ad i Bolme a bic di a bi c di c di c di ac bdc2 d2 bc adc2 d2 i displaystyle frac a bi c di frac a bi c di c di c di frac ac bd c 2 d 2 left frac bc ad c 2 d 2 right i Kompleks ededlere aid misallarToplama 3 2i 5 5i 3 5 2 5 i 8 7i displaystyle 3 2 mathrm i 5 5 mathrm i 3 5 2 5 mathrm i 8 7 mathrm i Cixilma 5 5i 3 2i 5 3 5 2 i 2 3i displaystyle 5 5 mathrm i 3 2 mathrm i 5 3 5 2 mathrm i 2 3 mathrm i Vurma 2 5i 3 7i 2 3 5 7 2 7 5 3 i 29 29i displaystyle 2 5 mathrm i cdot 3 7 mathrm i 2 cdot 3 5 cdot 7 2 cdot 7 5 cdot 3 mathrm i 29 29 mathrm i 1 i Modul 6 8i 62 82 36 64 100 10 displaystyle 6 8 mathrm i sqrt 6 2 8 2 sqrt 36 64 sqrt 100 10 ResursRiyazi istinadlari Conway John B Functions of One Complex Variable I Springer 1986 ISBN 0 387 90328 3 Press WH Teukolsky SA Vetterling WT Flannery BP Section 5 5 Complex Arithmetic Numerical Recipes The Art of Scientific Computing 3rd New York Cambridge University Press 2007 ISBN 978 0 521 88068 8 Tarixi istinadlari Nahin Paul J An Imaginary Tale The Story of 1 displaystyle scriptstyle sqrt 1 hardcover Princeton University Press 1998 ISBN 0 691 02795 1 A gentle introduction to the history of complex numbers and the beginnings of complex analysis H D Ebbinghaus Numbers hardcover Springer 1991 ISBN 0 387 97497 0 An advanced perspective on the historical development of the concept of number Xarici kecidlerVikianbarda Komplexe Zahlen ile elaqeli mediafayllar var at Convergence MAA Mathematical Sciences Digital Library John and Betty s Journey Through Complex Numbers Dimensions a math film Wikibooks Komplexe Zahlen Geschichte der komplexen Zahlen Eine Facharbeit die eine Einfuhrung in die komplexen Zahlen gibt Rechnen mit komplexen Zahlen Dimensions a math film Einbettung der komplexen Zahlen in die Darstellung hoherer Dimensionen auch Chaostheorie insb Kapitel 5 und 6 Java Applet zur geometrischen Deutung 2013 04 13 at the Wayback Machine Java Klasse zur Berechnung komplexer Zahlen Rechner fur komplexe Zahlen
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State