Natural loqarifm

Natural loqarifm — əsası e olan loqarifm. Burada e — irrasional sabitdir və təxminən 2,718281828-ə bərabərdir. Natural loqarifm adətən ln (x) kimi işarələnir. Həmçinin log_e (x) və ya əgər e əsası nəzərdə tutulursa, sadəcə log("x") kimi işarələnir. e (ln (e) ) ədədinin natural loqarifm vahidə bərabərdir, çünki e¹ = e. Vahidin natural loqarifmi (ln (1) ) sıfıra bərabərdir, çünki e⁰ = 1-dir. Loqarifmin tərifinə görə istənilən əsaslı vahidin loqarifmi sıfıra bərabərdir.

Natural loqarifm funksiyasının qrafiki. Funksiya x artımı anında yavaş-yavaş müsbət sonsuzluğa yaxınlaşır. "x" sıfır olduqda isə mənfi sonsuzluğa doğru sürətlə yaxınlaşır ("yavaş-yavaş" və "sürətlə" kəlmələri istənilən digər funksiya ilə müqayisədə işlənmişdir).

Natural loqarifm y= 1/x əyrisi altındakı sahədə 1-dən a-ya qədər olan istənilən müsbət həqiqi ədəd kimi müəyyən edilə bilər. Bu təyinin sadəliyi, başqa düsturlarla da uyğun gəlir. Bu düsturların bir çoxunda natural loqarifm tətbiq olunur. Bu təyinlərə əsasən e əsaslı loqarifmə "natural" loqarifm deyilir. Bu tərifi kompleks ədədlərdə də istifadə etmək olar.

Əsas natural loqarifmik eyniliklər:

${\displaystyle e^{\ln {a}}=a\quad (a>0)}$

Qeyd: Ümumiyyətlə bu eynilik əsas loqarifmik eynilik sayılır:${\displaystyle {a^{\log _{a}b}}=b}$

${\displaystyle \ln(e^{a})=a}$

İsbatı: ${\displaystyle \ln(e^{a})=a\cdot {\ln {e}}=a}$

Bütün loqarifmlərdə olduğu kimi, hasilin natural loqarifmi vuruqların loqarifmləri cəminə bərabərdir:

${\displaystyle \ln(xy)=\ln(x)+\ln(y)\!\,}$

Beləliklə, loqarifmik funksiyaların vurulması (müsbət ədədlər qrupu), bu funksiyalarının toplanması (həqiqi ədədlər qrupu) ilə izomorfizm təşkil edir. Bunu funksiya kimi belə təsvir etmək olar:

${\displaystyle \ln :\mathbb {R} ^{+}\to \mathbb {R} .}$

İstənilən əsasdan 1-dən başqa istənilən ədədin loqarifmini təyin etmək mümkündür. Loqarifmlər bir çox tənliklərin həllində istifadə edilir. Xüsusən də naməlum obyektin dərəcə göstəricisi kimi istifadə edilir. Məsələn, loqarifmlər məlum yarımparçalanma dövrü üçün və ya radioaktivlik məsələlərinin həllində parçalanma zamanın tapılması, parçalanma sabitinin tapılması üçün istifadə olunur. Loqarifmlər riyaziyyat və tətbiqi elmlərin bir çox sahələrində mühüm rol oynayır. Bir çox məsələlərin həllində - maliyyə sahəsində, mürəkkəb faizlərin tapılması kimi əməliyyatlarda istifadə edilir.

Tarixi

Natural loqarifm birinci dəfə Nikolas Merkator tərəfində 1668-ci ildə dərc edilmiş Logarithmotechnia əsərində qeyd etmişdir. Hərçənd ki, hələ 1619-cu ildə riyaziyyat müəllimi olan Con Spaydell natural loqarifmlərın cədvəlini qurmuşdu. Əvvəllər bu loqarifmi hiperbolik loqarifm adlandırırdılar, çünki natural loqarifm hiperbolain altındakı sahədə təyin olunur. Bəzən bu loqarifmi Nepera loqarifmi da adlandırırlar.

Yazılış müxtəlifliyi

Sovet sistemi

Natural loqarifmin "ln (x)" yazılışı qəbul edilmişdir. Əsası 10 olan onluq loqarifm — "lg (x)" vasitəsilə və başqa əsaslar "log" simvolu ilə yazılış qəbul edilmişdir.

Diskret riyaziyyat, kibernetika, informatika müəlliflərinin bir çoxu əsası 2 olan loqarifmlər üçün "log (x)" işarəsindən istifadə edirlər, amma bu yazılış hamı tərəfindən qəbul edilməyib və izah olunmayıb.

Loqarifm arqumenti mötərizə daxilində (əgər bu düsturun səhv oxumasına gətirmirsə) yazılır. Loqarifmik ifadələrin qüvvətini bilavasitə loqarifmin işarələrinə yazırlar: ln² ln³ 4x⁵ = [ln ( [ln (4x⁵)] ³)] ².

İngilis-Amerikan sistemi

Riyaziyyat, statistika və mühəndislikə adətən natural loqarifm "ln (x)" və ya "log (x)" işarəsi ilə yazılır. Əsası 10 olan onluq loqarifm — "log₁₀ (x)" kimi yazılır.

Bəzi mühəndislər, bioloqlar və mütəxəssislər həmişə "ln(x)" yazırlar (bəzən "log_e (x)"). Onlar əsasın natural (və ya onluq) loqarifm olduğunu nəzərdə tutaraq "log (x)" işarəsindən də istifadə edirlər.

Nəzəri informatikada, məlumat nəzəriyyəsində "log (x)" kriptoqrafiyası adətən əsası 2 olan ( "log₂ (x)") loqarifmi bildirir.

Texnika

Ən çox istifadə edilən proqramlaşdırma dillərində və tətbiqi proqramlar paketləri olan C, C++, SAS, MATLAB, Fortran və Basic "log" və ya "LOG" funksiyaları natural loqarifmə aiddir.

Adi kalkulyatorlarda natural loqarifm ln kimi işarə edilir. Burada log əsası 10 olan loqarifmin işarəsidir.

Xüsusi halları

• ${\displaystyle \ln(1)=0}$ 
• ${\displaystyle \ln(-1)=i\pi }$ 

(kompleks loqarifm)

• ${\displaystyle \ln(x)<\ln(y)\quad {\text{for}}\quad 0<x<y}$ 
• ${\displaystyle {\frac {h}{1+h}}\leq \ln(1+h)\leq h\quad {\text{for}}\quad h>-1}$ 
• ${\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1.}$ 

Natural loqarifm terminin mənşəyi

Əvvəla onu demək olar ki, hal-hazırda biz onluq say sistemindən istifadə edirik və bu əsas e əsasından daha da naturaldır. Lakin 10 riyazi ədədinin ayrıca əhəmiyyəti yoxdur. Bu əsas ən çox məişətdə istifadə olunur. Bu əsas bir çox hesablama sistemləri üçün ümumidir. Bu fikri insan barmaqlarının 10 ədəd olması ilə bağlayırlar. Bəzi sivilizasiyalar başqa əsaslar ilə öz hesablama sistemlərini qurmuşdur: 2, 5, 8, 12, 20 və 60.

log_e loqarifmi isə "natural" loqarifmdir, çünki, bu əsas riyaziyyatda çox sıx rast gəlinir. Məsələn, loqarifmik funksiyasının törəmə probleminə baxaq:

${\displaystyle {\frac {d}{dx}}\log _{b}(x)={\frac {d}{dx}}\left({\frac {1}{\ln(b)}}\ln {x}\right)={\frac {1}{\ln(b)}}{\frac {d}{dx}}\ln {x}={\frac {1}{x\ln(b)}}}$ 

Əgər b əsası e-yə bərabərdirsə, onda törəmə sadəcə 1/x-ə bərabərdir və x = 1 olduqda bu törəmə vahidə bərabərdir. Başqa əsaslandırılma, loqarifm e əsasında ən "naturaldır", bunu sadəcə inteqralın və ya bir sıra Teylor terminləri ilə təyin etmək olar. Bu fikri başqa loqarifmlər haqqında demək olmaz.

Naturallığın bir sonrakı əsaslandırılması hesablamayla bağlı deyildir. Belə ki, məsələn, natural loqarifmlərlə bağlı bir neçə sadə sıra var idi. Petro Menqoli və Nikolay Merkator bu sıranı loqarifmus naturalis bir neçə onluq sırası adlandırırdı. Lakin, o vaxtı hələ Nyuton və Leybnits diferensialı kəşf edilməşdir və inteqral hesablamadan istifadə olunmurdu.

Təyini

 

ln(a), f (x)= 1 əyrisinin altındakı sahədə 1-dən a-ya kimi təyin edilir

Adətən ln (a) qrafikdə 1/x əyrisi altındakı sahədə 1-dən a-ya qədər təyin olunur, yəni inteqralı aşağıdakı kimidir:

${\displaystyle \ln(a)=\int _{1}^{a}{\frac {1}{x}}\,dx.}$ 

Natural loqarifm, həqiqətən də loqarifmdır, çünki natural loqarifm, loqarifmin fundamental xüsusiyyətlərinə cavab verir:

${\displaystyle \ln(ab)=\ln(a)+\ln(b)}$ 

Bunu göstərmək üçün 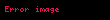${\displaystyle t={\tfrac {x}{a}}}$  olduğunu güman edib, aşağıdakı qaydanı yerinə yetirmək lazımdır:

${\displaystyle \ln(ab)=\int _{1}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{a}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{t}}\;dt=\ln(a)+\ln(b)}$ 

ln (a) = 1 olduqda e ədədi a-nın yeganə həqiqi ədədi kimi təyin olunur.

Yaxud, əgər nümunəvi funksiya əvvəl mənfi sonsuz sıralarda təyin olunursa, natural loqarifm ona əks funksiyadır, yəni ${\displaystyle e^{\ln(x)}=x\!}$ . Çünki həqiqi arqumentlərin, səciyyəvi funksiyanın qiymətlər oblastında bütün müsbət həqiqi ədədləri mövcuddur. Səciyyəvi funksiya artandır və bütün müsbət x-lər üçün təyin olunan funksiyadır.

Törəmə, Teylor sırası

 

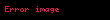Teylor çoxhədliləri ${\displaystyle \ln(1+x)\,}$  üçün yalnız - 1 < x ≤ 1 oblastında dəqiq yaxınlaşmanı verir. Qeyd edək ki, x > 1 olduqda Teylor çoxhədlisi zəif yaxınlaşmasını verir.

Natural loqarifmin törəməsi:

${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}}.}$ 

Buna əsasən 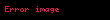${\displaystyle \ln(1+x)\,}$  ayrılışını yerinə yetirmək olar və Teylor təxminən 0 ətrafında qiymət alır və bu Merkator sırası adlandırılır:

${\displaystyle \ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\dots \quad {\text{for}}\quad \left|x\right|\leq 1\quad }$ 

${\displaystyle {\text{unless}}\quad x=-1}$ 

Sağda təsvir edilmiş 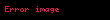${\displaystyle \ln(1+x)\,}$  və başqa Teylor çoxhədliləri 0 ətrafında qiymət alır. Bu yaxınlaşma yalnız - 1 < x ≤ 1 oblastında mümkümdür və bu hüdudlar xaricində yüksək dərəcəli Teylor çoxhədliləri daha az dəqiq yaxınlaşma verir. x-in yerinə x-1 qoysaq, ln (x) üçün alternativ formanı alaq:

${\displaystyle \ln(x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}(x-1)^{n}}$ 

${\displaystyle \ln(x)=(x-1)-{\frac {(x-1)^{2}}{2}}+{\frac {(x-1)^{3}}{3}}-{\frac {(x-1)^{4}}{4}}+\dots }$ 

${\displaystyle {\text{for}}\quad \left|x-1\right|\leq 1\quad {\text{unless}}\quad x=0.}$ 

Bir sıra Merkator Eyler dəyişikliyinin köməyi ilə aşağıdakı ifadəni almaq olar (yalnız x>1 olduğu halda):

${\displaystyle \ln {x \over {x-1}}=\sum _{n=1}^{\infty }{1 \over {nx^{n}}}={1 \over x}+{1 \over {2x^{2}}}+{1 \over {3x^{3}}}+\dots }$ 

Bu sıra Beyli — Borueyn — Plaffa düsturuna oxşardır.

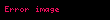
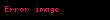
Həmçinin onu da qeyd edək ki, ${\displaystyle x \over {x-1}}$  — bu xüsusi inverik funksiyadır, buna görə də y-in müəyyən ədədinin natural loqarifminin alınması üçün sadəcə x-ə ${\displaystyle y \over {y-1}}$  qiymətini mənimsətmək lazımdır.

Natural loqarifmin inteqralı

Natural loqarifm g (x)= f(x) /f (x) növünün sadə inteqral funksiyasını verir: g (x) funksiyaları ln(|f(x)|) funksiyalarına bənzəyir. Bu zəncir qaydası ilə və aşağıdakı faktla təsdiq edilir:

${\displaystyle \ {d \over dx}\left(\ln \left|x\right|\right)={1 \over x}.}$ 

Başqa növ:

${\displaystyle \int {1 \over x}dx=\ln |x|+C}$ 

və

${\displaystyle \int {{\frac {f'(x)}{f(x)}}\,dx}=\ln |f(x)|+C.}$ 

Aşağıda g (x)=tan(x) üçün nümunə verilmişdir:

${\displaystyle \int \tan(x)\,dx=\int {\sin(x) \over \cos(x)}\,dx}$ 

${\displaystyle \int \tan(x)\,dx=\int {-{d \over dx}\cos(x) \over {\cos(x)}}\,dx.}$ 

Tutaq ki, f (x) = cos (x) və f'(x) = - sin (x):

${\displaystyle \int \tan(x)\,dx=-\ln {\left|\cos(x)\right|}+C}$ 

${\displaystyle \int \tan(x)\,dx=-\ln {\left|\cos(x)\right|}+C}$ 

${\displaystyle \int \tan(x)\,dx=\ln {\left|\sec(x)\right|}+C}$ 

burada C — sərbəst sabit həddir.

Natural loqarifmi hissə-hissə inteqrallama üsulu ilə inteqrallamaq olar:

${\displaystyle \int \ln(x)\,dx=x\ln(x)-x+C.}$ 

Ədədi qiyməti

Ədədin natural loqarifminin qiymətinin hesablaması üçün sıra şərtini gözləməklə Teylor üsulundan istifadə etmək olar:

${\displaystyle \ln(1+x)=x\,\left({\frac {1}{1}}-x\,\left({\frac {1}{2}}-x\,\left({\frac {1}{3}}-x\,\left({\frac {1}{4}}-x\,\left({\frac {1}{5}}-\dots \right)\right)\right)\right)\right)\quad {\text{for}}\quad \left|x\right|<1.}$ 

Bu prosesi daha tez etmək üçün aşağıdakı eynilikdən istifadə etmək olar:

${\displaystyle \ln(x)=\ln \left({\frac {1+y}{1-y}}\right)}$	${\displaystyle =2\,y\,\left({\frac {1}{1}}+{\frac {1}{3}}y^{2}+{\frac {1}{5}}y^{4}+{\frac {1}{7}}y^{6}+{\frac {1}{9}}y^{8}+\dots \right)}$
	${\displaystyle =2\,y\,\left({\frac {1}{1}}+y^{2}\,\left({\frac {1}{3}}+y^{2}\,\left({\frac {1}{5}}+y^{2}\,\left({\frac {1}{7}}+y^{2}\,\left({\frac {1}{9}}+\dots \right)\right)\right)\right)\right)}$

Qeyd:y = (x−1) / (x+1) və x > 0 şərtini gözləməklə.

ln (x) üçün x > 1 olduqda və x nə qədər 1-ə yaxın qiymət aldıqda bu proses sürətlə gedir. Həmçinin loqarifm ilə bağlı eyniliklərdən istifadə etmək olar:

${\displaystyle \ln(123{,}456)\!}$	${\displaystyle =\ln(1{,}23456\times 10^{2})}$
	${\displaystyle =\ln(1{,}23456)+\ln(10^{2})}$
	${\displaystyle =\ln(1{,}23456)+2\times \ln(10)}$
	${\displaystyle \approx \ln(1{,}23456)+2\times 2{,}3025851}$

Bu metodlar hələ kalkulyatorlar yaranmamışdan əvvəl tətbiq edilirdi. Bunun üçün yuxarıda göstərilən analoji ədəd cədvəllərindən istifadə olunurdu və manipulyasiyalar yerinə yetirilirdi.

Yüksək dəqiqlik

Kiçik miqyaslı dəqiqliklə natural loqarifmin hesablanması üçün bir Teylor üsulu əlverişli deyil və vaxt aparandır. Alternativ və səmərəli Nyuton üsulundan istifadə etmək olar.

Çox yüksək dəqiqlikli hesablanma üçün düstur:

${\displaystyle \ln x\approx {\frac {\pi }{2M(1,4/s)}}-m\ln 2}$ 

haradakı M - 1 və 4/s arifmetik-həndəsi ortasını ifadə edirsə və

${\displaystyle s=x\,2^{m}>2^{p/2},}$ 

m p dəqiqlik simvolunun təyini üçün istifadə edilir (adətən 8 qiyməti kifayət edir). Əslində, bu metodun istifadə olunması üçün səciyyəvi funksiyanın natural loqarifminə Nyuton inversiyası tətbiq etmək mümkün olmalıdır.

Hesablama çətinliyi

Natural loqarifmlərin (arifmetik-həndəsi ortanın köməyi ilə) hesablama çətinliyi O(M (n) ln n) bərabərdir. Burada n — dəqiqlik rəqəmlərinin sayıdır, hansının ki, natural loqarifminin qiyməti olmalıdır, və M (n) — iki n-rəqəmli ədədin vurulmasının hesablaması çətinliyidir.

Davamlı kəsrlər

Hərçənd ki, loqarifmin təsviri üçün sadə davamlı kəsr mövcud deyil, amma bir neçə ümumiləşmiş davamlı kəsrdən istifadə etmək olar:

${\displaystyle \log(1+x)={\frac {x^{1}}{1}}-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\dots ={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}}$ 

${\displaystyle \log \left(1+{\frac {2x}{y}}\right)={\cfrac {2x}{y+{\cfrac {x}{1+{\cfrac {x}{3y+{\cfrac {2x}{1+{\cfrac {2x}{5y+{\cfrac {3x}{1+\ddots }}}}}}}}}}}}={\cfrac {2x}{y+x-{\cfrac {(1x)^{2}}{3(y+x)-{\cfrac {(2x)^{2}}{5(y+x)-{\cfrac {(3x)^{2}}{7(y+x)-\ddots }}}}}}}}}$ 

Mənbə

1. Mortimer, Robert G. Mathematics for physical chemistry (3rd). Academic Press. 2005. səh. 9. ISBN 0-125 - 08347-5., Extract of page 9
2. J J O'Connor and E F Robertson. "The number e". The MacTutor History of Mathematics archive. 2001-09. 2012-02-11 tarixində arxivləşdirilib. İstifadə tarixi: 2013-12-08.
3. Cajori, Florian. A History of Mathematics, 5th ed. AMS Bookstore. 1991. 152. ISBN 0821821024.
4. Flashman, Martin. "Estimating Integrals using Polynomials". 2012 - 02-12 tarixində arxivləşdirilib.
5. Boyers, Carl. A History of Mathematics. John Wiley & Sons. 1968.
6. Harris, John. (PDF). Australian Aboriginal Studies. 2. 1987: 29–37. 2007-08-31 tarixində orijinalından (PDF) arxivləşdirilib. İstifadə tarixi: 2013-12-14.
7. Large, J.J. wid=636 "The vigesimal system of enumeration" (#bad_url). Journal of the Polynesian Society. 11 (4). 1902: 260–261.
8. Cajori first=Florian. "Sexagesimal fractions among the Babylonians". American Mathematical Monthly. 29 (1). 1922: 8–10. doi:10.2307/2972914. JSTOR 2972914. (#missing_pipe)
9. Larson, Ron. id=rbDG7V0OV34C Calculus: An Applied Approach (#bad_url) (8th). Cengage Learning. 2007. səh. 331. ISBN 0-618 - 95825-8. (#missing_pipe)
10. Ballew, Pat. "Math Words, and Some Other Words, of Interest". 2012-02-11 tarixində # ln orijinalından (#bad_url) arxivləşdirilib. İstifadə tarixi: 2020-09-16.
11. "Logarithmic Expansions" at Math2.org
12. Sasaki, T.; Kanada, Y. [http: //ci.nii.ac.jp / naid/110002673332 "Practically fast multiple-precision evaluation of log (x)"] (#bad_url). Journal of Information Processing. 5 (4). 1982: 247–250. İstifadə tarixi: 30 March 2011.
13. Ahrendt, Timm. "Fast computations of the exponential function". Lecture notes in computer science. 1564. 1999: 302–312. doi:10.1007/3-540-49116-3_28.