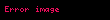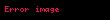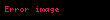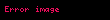Törəmə — funksiyanın hər hansı verilmiş bir nöqtədə dəyişmə sürətini göstərir. y=f(x) funksiyası hər hansı a nöqtəsində kəsilməzdirsə, arqumentin sonsuz kiçilən artımına funksiyanın da sonsuz kiçilən artımı uyğun olur ki, bu təklifin əksi də doğrudur. Yəni arqumentin a nöqtəsindəki sonsuz kiçilən artımına funksiyanın da bu nöqtədə sonsuz kiçilən artımı uyğundursa, funksiya bu nöqtədə kəsilməzdir. Arqument artımı sifra yaxınlaşdıqda funksiya artımının arqument artımına nisbətinin limiti varsa, bu limitə f(x) funksiyasının a nöqtəsində törəməsi deyilir. Əgər →0 şərtində

nisbətinin sonlu limiti varsa, onda həmin limitə y=f(x) funksiyasının x nöqtəsində törəməsi deyilir. Verilmiş x nöqtəsində törəməsi olan funksiyaya həmin nöqtədə diferensiallanan funksiya deyilir. (a, b) intervalının hər bir nöqtəsində törəməsi olan funksiya həmin intervalda diferensiallanan funksiya adlanır. Funksiyanın törəməsini tapmaq əməlinə həmin funksiyanın diferensiallanması deyilir.
Elementar funksiya törəmələri
- Eksponensial və alqoritmik funksiyalar:
- Triqonometriya funksiyaları:
- Tərs triqonometrik funksiyalar:
Törəmənin tətbiqi
Törəmənin sıfra bərabər olduğu və törəmənin olmadığı daxili nöqtələr funksiyanın böhran nöqtələridir. Həmin nöqtələr funksiyanın aldığı ən böyük və ya ən kiçik qiymətlər ola bilər. Bundan başqa cismin sürətinin zamana görə funksiyasının törəməsi onun təcilinə bərabərdir.
İstinadlar
Həmçinin bax
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Toreme funksiyanin her hansi verilmis bir noqtede deyisme suretini gosterir y f x funksiyasi her hansi a noqtesinde kesilmezdirse arqumentin sonsuz kicilen artimina funksiyanin da sonsuz kicilen artimi uygun olur ki bu teklifin eksi de dogrudur Yeni arqumentin a noqtesindeki sonsuz kicilen artimina funksiyanin da bu noqtede sonsuz kicilen artimi uygundursa funksiya bu noqtede kesilmezdir Arqument artimi sifra yaxinlasdiqda funksiya artiminin arqument artimina nisbetinin limiti varsa bu limite f x funksiyasinin a noqtesinde toremesi deyilir Eger Dx displaystyle Delta x 0 sertindeFunksiyanin qrafiki qara rengde ona toxunan duz xettin qrafiki ise qirmizi rengde gosterilmisdir Duz xettin qrafikinin funksiyanin qrafikine toxundugu noqtenin deyeri hemin toxunanin bucaq emsalina beraberdir DyDx f x Dx f x Dx displaystyle frac Delta y Delta x frac f x Delta x f x Delta x nisbetinin sonlu limiti varsa onda hemin limite y f x funksiyasinin x noqtesinde toremesi deyilir Verilmis x noqtesinde toremesi olan funksiyaya hemin noqtede diferensiallanan funksiya deyilir a b intervalinin her bir noqtesinde toremesi olan funksiya hemin intervalda diferensiallanan funksiya adlanir Funksiyanin toremesini tapmaq emeline hemin funksiyanin diferensiallanmasi deyilir Elementar funksiya toremeleriEksponensial ve alqoritmik funksiyalar ddxex ex displaystyle frac d dx e x e x ddxax ln a ax displaystyle frac d dx a x ln a a x ddxln x 1x x gt 0 displaystyle frac d dx ln x frac 1 x qquad x gt 0 ddxloga x 1xln a displaystyle frac d dx log a x frac 1 x ln a Triqonometriya funksiyalari ddxsin x cos x displaystyle frac d dx sin x cos x ddxcos x sin x displaystyle frac d dx cos x sin x ddxtan x sec2 x 1cos2 x 1 tan2 x displaystyle frac d dx tan x sec 2 x frac 1 cos 2 x 1 tan 2 x Ters triqonometrik funksiyalar ddxarcsin x 11 x2 1 lt x lt 1 displaystyle frac d dx arcsin x frac 1 sqrt 1 x 2 1 lt x lt 1 ddxarccos x 11 x2 1 lt x lt 1 displaystyle frac d dx arccos x frac 1 sqrt 1 x 2 1 lt x lt 1 ddxarctan x 11 x2 displaystyle frac d dx arctan x frac 1 1 x 2 Toremenin tetbiqiToremenin sifra beraber oldugu ve toremenin olmadigi daxili noqteler funksiyanin bohran noqteleridir Hemin noqteler funksiyanin aldigi en boyuk ve ya en kicik qiymetler ola biler Bundan basqa cismin suretinin zamana gore funksiyasinin toremesi onun teciline beraberdir IstinadlarHemcinin baxTeylor teoremi Differensial riyaziyyat
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State