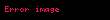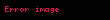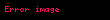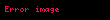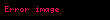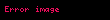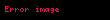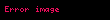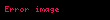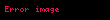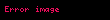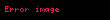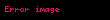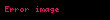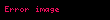İnteqral

İnteqral – kəsilməz f(x) funksiyasının ibtidai funksiyalarının ümumi şəklinə f(x) funksiyasının inteqralı deyilir.

f(x)-in a dan b'yə qədər olan inteqralı, y=f(x) funksiyasının a ilə b arasındakı fiqurun sahәsinә bәrabәrdir.

Tarixi

İnteqral sahəsində ən böyük işləri Qotfrid Leybnits və İsaak Nyuton görmüşlər. "İnteqral" sözünü və işarəsini ilk dəfə elmə alman alimi Qotfrid Leybnits daxil etmişdir. Bu söz latıncadan "Cəm" ("ſumma", "summa") mənasını verir. İnteqral ∫ hərfi ilə işarə edilir:

${\displaystyle F(x)=\int f(x)+c,}$

[a, b] parçasında götürülmüş f(x) funksiyasının müəyyən inteqralın düsturu belədir:

${\displaystyle \int _{a}^{b}\!f(x)\,dx\,}$

Qeyri-müəyyən inteqralın isə düsturu belədir:

${\displaystyle F=\int f(x)\,dx+c}$

İnteqral hesabına aid nümunə

${\displaystyle f(x)=5x^{2}+9x+15\,}$.

${\displaystyle f'(x)=10x+9+0\,}$.

${\displaystyle \int (10x+9)\,dx=5x^{2}+9x+C}$.

Bəsit funksiyaların inteqralları

Rasional funksiyalar

${\displaystyle \int dx=x+C}$

${\displaystyle \int {dx \over x}=\ln {\left|x\right|}+C}$

${\displaystyle \int {dx \over {a^{2}+x^{2}}}={1 \over a}\arctan {x \over a}+C}$

İrrasional funksiyalar

${\displaystyle \int {dx \over {\sqrt {a^{2}-x^{2}}}}=\arcsin {x \over a}+C}$

${\displaystyle \int {-dx \over {\sqrt {a^{2}-x^{2}}}}=\arccos {x \over a}+C}$

${\displaystyle \int {dx \over x{\sqrt {x^{2}-a^{2}}}}={1 \over a}\sec {|x| \over a}+C}$

Loqarifmik funksiyalar

${\displaystyle \int \ln(x)\,dx=x\ln(x)-x+C,}$

${\displaystyle \int \log _{b}{x}\,dx=x\log _{b}{x}-x\log _{b}{e}+C}$:)

Üstlü funksiyalar

${\displaystyle \int e^{x}\,dx=e^{x}+C}$

${\displaystyle \int a^{x}\,dx={\frac {a^{x}}{\ln {a}}}+C}$

${\displaystyle \int a^{ln(x)}\,dx=\int x^{ln(a)}\,dx={\frac {x\,a^{ln(x)}}{\ln {a}+1}}+C={\frac {x\,x^{ln(a)}}{\ln {a}+1}}+C}$

Triqonometrik funksiyalar

Qotfrid Leybnits

Ser İsaak Nyuton

${\displaystyle \int \sin {x}\,dx=-\cos {x}+C}$

${\displaystyle \int \cos {x}\,dx=\sin {x}+C}$

${\displaystyle \int \tan {x}\,dx=-\ln {\left|\cos {x}\right|}+C}$

${\displaystyle \int \cot {x}\,dx=\ln {\left|\sin {x}\right|}+C}$

${\displaystyle \int \sec {x}\,dx=\ln {\left|\sec {x}+\tan {x}\right|}+C}$

${\displaystyle \int \csc {x}\,dx=\ln {\left|\csc {x}-\cot {x}\right|}+C}$

${\displaystyle \int \sec ^{2}x\,dx=\tan x+C}$

${\displaystyle \int \csc ^{2}x\,dx=-\cot x+C}$

${\displaystyle \int \sec {x}\,\tan {x}\,dx=\sec {x}+C}$

${\displaystyle \int \csc {x}\,\cot {x}\,dx=-\csc {x}+C}$

${\displaystyle \int \sin ^{2}x\,dx={\frac {1}{2}}(x-\sin x\cos x)+C}$

${\displaystyle \int \cos ^{2}x\,dx={\frac {1}{2}}(x+\sin x\cos x)+C}$

${\displaystyle \int \sec ^{3}x\,dx={\frac {1}{2}}\sec x\tan x+{\frac {1}{2}}\ln |\sec x+\tan x|+C}$

${\displaystyle \int \sin ^{n}x\,dx=-{\frac {\sin ^{n-1}{x}\cos {x}}{n}}+{\frac {n-1}{n}}\int \sin ^{n-2}{x}\,dx}$

${\displaystyle \int \cos ^{n}x\,dx={\frac {\cos ^{n-1}{x}\sin {x}}{n}}+{\frac {n-1}{n}}\int \cos ^{n-2}{x}\,dx}$

${\displaystyle \int \arctan {x}\,dx=x\,\arctan {x}-{\frac {1}{2}}\ln {\left|1+x^{2}\right|}+C}$

Hiperbolik funksiyalar

${\displaystyle \int \sinh x\,dx=\,coshx+C}$

${\displaystyle \int \cosh x\,dx=\sinh x+C}$

${\displaystyle \int \tanh x\,dx=\ln |\cosh x|+C}$

${\displaystyle \int {\mbox{csch}}\,x\,dx=\ln \left|\tanh {x \over 2}\right|+C}$

${\displaystyle \int {\mbox{sech}}\,x\,dx=\arctan(\sinh x)+C}$

${\displaystyle \int \coth x\,dx=\ln |\sinh x|+C}$

${\displaystyle \int {\mbox{sech}}^{2}x\,dx=\tanh x+C}$

Tərs hiperbolik funksiyalar

${\displaystyle \int \operatorname {arcsinh} x\,dx=x\operatorname {arcsinh} x-{\sqrt {x^{2}+1}}+C}$

${\displaystyle \int \operatorname {arccosh} x\,dx=x\operatorname {arccosh} x-{\sqrt {x^{2}-1}}+C}$

${\displaystyle \int \operatorname {arctanh} x\,dx=x\operatorname {arctanh} x+{\frac {1}{2}}\log {(1-x^{2})}+C}$

${\displaystyle \int \operatorname {arccsch} \,x\,dx=x\operatorname {arccsch} x+\log {\left[x\left({\sqrt {1+{\frac {1}{x^{2}}}}}+1\right)\right]}+C}$

${\displaystyle \int \operatorname {arcsech} \,x\,dx=x\operatorname {arcsech} x-\arctan {\left({\frac {x}{x-1}}{\sqrt {\frac {1-x}{1+x}}}\right)}+C}$

${\displaystyle \int \operatorname {arccoth} \,x\,dx=x\operatorname {arccoth} x+{\frac {1}{2}}\log {(x^{2}-1)}+C}$

Xarici keçidlər

• Wolfram Integrator