Bütöv mühit mexanikası mexanikanın bir bölməsi olub materialların mexaniki xassəsini və kinematik analizini öyrənir. Materiallar diskret paylanmış hissəciklər şəklində yox, bütöv (arasıkəsilməz paylanmış) kütlə şəklində modelləşdirilir. Belə bir model ilk dəfə XIX əsrdə Fransız riyaziyyatçısı Auqusto Koşi (fr. Augustin Louis Cauchy) tərəfindən ifadə edilmişdir, amma tədqiqatlar bu gün də davam etdirilir.
| Bütöv mühit mexanikası | ||||||||||
 | ||||||||||
| ||||||||||
Qısa şərh
| Klassik mexanika | ||||||||
 (Nyutonun ikinci qanunu) | ||||||||
| ||||||||
Bir obyektin bütöv cisim şəklində modelləşdirilməsi dedikdə obyekti təşkil edən cismin obyektin tutduğu fəzanı tamamilə doldurması fərziyyəsi nəzərdə tutulur. Obyektin belə modelləşdirilməsi maddənin atomlardan təşkil olunmasını və beləliklə bütöv olmamasını nəzərə almır. Buna baxmayaraq atomlar arası məsafələrdən qat-qat böyük ölçü miqyaslarında belə modellər olduqca dəqiqdir. Belə obyektlərin xassəsini təsvir edən çıxarılması üçün , və kimi özül fizika qanunlarını belə modellərə tətbiq etmək olar.
Bütöv mühit mexanikası bərk, maye və qazların fiziki xassələrini onların müşahidə edildiyi istənilən xüsusi koordinat sistemindən asılı olmadan öyrənir. Beləliklə, bu fiziki xassələr tenzorlarla ifadə edilir ki, tenzorlar tələb olunan xassəyə malik riyazi predmet olub koordinat sistemindən asılı deyildir. Bu tenzorlar hesablamanı asanlaşdırmaq üçün koordinat sistemləri ilə də ifadə oluna bilər.
Anlayış
Bərk, maye və qazlar kimi materiallar "boş" fəza ilə bir-birindən ayrılmış molekullardan təşkil olunub. Mikroskopik ölçüdə, materiallarda çatlar və kəsilmələr (materialın bütöv və davamlı olmaması, onlarda qüsurların olması nəzərdə tutulur) mövcuddur. Buna baxmayaraq, müəyyən fiziki hadisələr "bütöv mühit - cisimdəki maddə miqdarı kəsilməz yayılmışdır və cismin tutduğu fəzanı tamamilə doldurur deməkdir" fərziyyəsi qəbul olunmaqla modelləşdirilə bilər. Bir bütöv mühit elə bir cisimdir ki, o davamlı olaraq çox kiçik elementlərə bölündükdə belə, bu kiçik hissəciklər əsas cismin xassələrini özündə saxlayır.
Bütöv mühit mexanikasının əsas sahələri
| Bütöv mühit mexanikası Bütöv (kəsilməz) materialların fizikasını öyrənən elm | Müəyyən olunmuş dayanıqlı formaya malik bütöv materialların fizikasını öyrənən elm. | Elastiklik Tətbiq olunmuş gərginliklər götürüldükdən sonra materialın dayanıqlı vəziyyətinə qayıtmasını təsvir edir. | |
| Plastiklik Kifayət həddə qüvvə tətbiq edildikdə qalıq deformasiyaya uğrayan materialları təsvir edir. | Reologiya Bərk və maye xüsusiyyətinə malik materialları öyrənən elm . | ||
Qüvvə tətbiq olunduqda formasını dəyişən bütöv materialların fizikasını öyrənən elm. | tətbiq olunmuş kəsici gərginliyə mütənasib olaraq nisbi deformasiya tezliyinə məruz qalmır. | ||
| tətbiq olunmuş kəsici gərginliyə mütənasib olaraq nisbi deformasiya tezliyinə məruz qalır. | |||
Modelin ifadə olunması

Bütöv mühit mexanikası modeli, modelləşdiriləcək material cisim 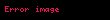

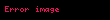
Cisim daxilindəki hər hansı bir hissəciyin müəyyən bir konfiqurasiyada vəziyyəti radius-vektoru ilə ifadə edilir
Burada 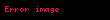
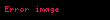
Bu funksiya fiziki məna verməsi üçün müxtəlif xassəllərə malik olmalıdır. 
- zamanda kəsilməzdir, yəni cisimin dəyişməsi reallığı əks edirir,
- istənilən bütün zaman kəsiyində tərs funksiyasına malikdir, yəni cisimdə heç bir hissəcik yox olmur və ya yenisi yaranmır (riyazi olaraq bu, hissəciklərin deformasiya olunmuş və deformasiya olunmamış konfiqurasiyalarda birin-birə əlaqələrinin olmasını nəzərdə tutur),
- dəyişməz oriyentasiyalıdır, yəni təbiətdə heç bir tansformasiya cisimdə güzgü əksi yaratmır.
Modelin riyazi ifadəsi üçün, 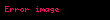
Bütöv mühitdə qüvvələr
Bütöv mühit mexanikası mütləq bərk cisminlərin əksinə deformasiya olunan cisimlərlə məşğuldur. Bərk cisim deformasiya oluna bilən cisim olub kəsici müqavimətə, yəni kəsici qüvvələrə (cismin səthinə parallel təsir göstərən qüvvə nəzərdə tutulur) qarşı müqavimətə, malikdir. Anacaq mayelər belə müqavimətə malik deyillər. Maye və bərk cisimləri tədqiq etmək üçün onların bütöv olması fərz olunur, yəni onların həcimlərinin, tutduqları fəzanın bütün sahəsini doldurması nəzərdə tutulur. Ona görə də, bütov mühit mexanikasında cisimdəki nöqtə və ya hissəcikdən danışıldıqda bu hər hansı bir atom hissəciyi və ya atom miqyasında bir nöqtə deyil, bu nöqtəni əhatə edən cismin ideallaşdırılmış bir hissəsi nəzərdə tutulur.
Nyuton və Eyler-in klassik dinamikasına əsaslanaraq, bir maddi cismin hərəkəti ona tədbiq olunmuş xarici qüvvələrin təsirindən yaranır. Bu qüvvələrin iki cür: səthi qüvvələr 


Səthi qüvvələr
və ya təmas qüvvələri vahid sahəyə düşən qüvvə kimi ifadə olunur. Bu qüvvələr ya bir cismin başqa cisimlərlə təması nəticəsində onun sərhəd səthinə, ya da bir cismin hissələri arasındakı mexaniki qarşılıqlı təsiri nəticəsinə təsir səthinin hər iki tərəfinə təsir göstərə bilər. Bir cismə xarici təmas qüvvələri təsir etdikdə, bu zaman daxili təmas qüvvəlləri Nyutonun üçüncü hərəkət qanuna və eləcədə bucaq momentinin və xətli momentin saxlanması qanunlarına görə cisim daxilində nöqtədən nöqtəyə ötürülməklə müvazinətləşir (bütöv mühit mexanikasında bu qanunlar Eylerin hərəkət qanunları adlandırılır). Daxili təmas qüvvələri, material tənlikləri (materialın fiziki xarakteristikasını məs. elatiklik, plastiklik və s. təyin edən tənliklər) vasitəsilə cismin deformasiyası ilə əlaqələndirilir.
Daxili qüvvələrin cismin bütün həcmində kəsilməz olaraq yayılması fərz edilir. Beləliklə, daxili qüvvələr təmas qüvvə sıxlığı və ya Koşi dartma sahəsi 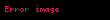
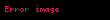

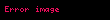

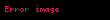
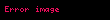
Verilmimş bir daxili 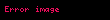



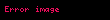
.
Burada 
Xüsusi səthdəki yekun təmas qüvvəsi 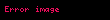

Bütöv mühit mexanikasında bir cisim o halda gərginliksiz hesab edilir ki, yeganə mövcud qüvvəllər atomlar arası (ionik, metalik, və Van-der-Vaals) qüvvələrdir ki, bu qüvvələr də bütün xarici təsirlərin (yerin cazibə qüvvəsi də bura daxildir) yoxluğunda, cismin özünü saxlaması və formasını qoruması üçün vacibdir. Cismin istehsalı zamanı yaranan gərginliklər də, hesablanma zamanı istisna edilir. Beləliklə, bütöv mühit mexanikasında gərginliklər adətən qəbul olunmuş ilkin konfiqurasiyaya nəzərən deformasiyanın yaratdığı gərginlikləri nəzərdə tutur. Başqa sözlə, cisimdəki gərginliyin mütləq (gerçək) qiymətinə deyil, yalnız gərginlikdəki nisbi dəyişmələrə baxılır.
Həcmi qüvvələr
cismin həcminə (və ya kütləsinə) xaricdən təsir göstərən qüvvələrdir. Həcmi qüvvələrin xaricdən təsir edən qüvvələr olduğunu deməklə, biz fərz edirik ki, cismin müxtəlif hissələri arasındakı qarşılıqlı təsir (daxili qüvvələr) yalnız təmas (kontakt) qüvvələri ilə verilir. Həcmi qüvvələr cismin, məs. qravitasiya sahəsi, elektrik sahəsi və ya maqnit sahəsi kimi qüvvə sahələrində yerləşməsindən yaranır. Bütöv cismin kütləsinin kəsilməz paylandığı fərz edildiyindən, bu kütlədən qaynaqlanan istənilən qüvvə də kəsilməz paylanacaqdır. Beləliklə, həcmi qüvvələr cismin bütün həcmi üzrə kəsilməz olan, yəni cismin hər bir nöqtəsinə təsir edən, vektor sahələri ilə verilir. Həcmi qüvvələr həcmi qüvvə sıxlığı (vahid kütləyə düşən qüvvə) 
Həcmi qüvvələr qravitasiya qüvvələri olduqda, bu qüvvənin intensivliyi materialın kütlə sıxlığı 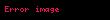

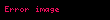
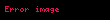
Bir bütöv cismə təsir göstərən bütün həcmi qüvvələr belə təsvir edilir
Cismə təsir göstərən həcmi qüvvələr və təmas qüvvələri müəyyən bir nöqtəyə nəzərən müvafiq qüvvə momentləri (fırladıcı momentlər) yaradır. Beləliklə, bütün tətbiq olunmuş fırladıcı moment 
Kinematika: hərəkət və deformasiya

Bütöv cismin konfiqurasiyasının dəyişməsi sahəsi ilə təsvir edilir. Cismin yerdəyişməsinin iki tərkib hissəsi mövcuddur: mütləq-cisim yerdəyişməsi və deformasiya. Mütləq-cisim yerdəyişməsi, cismin forma və ölçülərini dəyişməyən eyni anda baş verən irəlilləmə və fırlanma hərəkətlərindən təşkil olunur. Deformasiya, cismin başlanğıc vəziyyətinə nəzərən forma və ya ölçülərini dəyişməsini bildirir. Cismin başlanğıc vəziyyəti onun başlanğıc və ya istinad konfiqurasiyası (
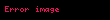
Bütöv bir cismin hərəkəti yerdəyişmələrin zamanda kəsilməz ardıcıllığından ibarətdir. Beləliklə, material cisim müxtəlif zaman anlarında müxtəlif konfiqurasiyaları tutur ki, cismin istənilən bir hissəciyi də fəzada uyğun olaraq müəyyən nöqtələr sırasınında yerini dəyişir. Bu nöqtələr sırası həmin hissəciyin trayektoriyasını təsvir edir.
Bütöv cisimin deformasiyası və ya hərəkəti ərzində aşağıdakı mənada kəsilməzlik vardır:
- İstənilən bir zaman anında qapalı bir əyri meydana gətirən material nöqtələri, sonrakı istənilən zaman ardıcıllığına da həmişə qapalı bir əyri meydana gətirəcəklər.
- İstənilən bir zaman anında qapalı bir səth meydana gətirən material nöqtələri, sonrakı istənilən zaman ardıcıllığında da həmişə qapalı bir səth meydana gətirəcəklər və bu qapalı səth daxilindəki maddə həmişə bu səth daxilində qalacaqdır.
Əsas tənliklər
Bütöv mühit mexanikası materialların xassələri ilə məşğul olur ki, onlar müəyyən uzunluq və zaman miqyasları üçün kəsilməz olaraq təqribi hesablana bilər. Materialların mexanikasını təyin edən belə tənliklərə , və üçün müvazinət (balans və ya saxlanma) qanunları daxildir. Əsas (idarəedici) tənliklər sistemini tamlamaq üçün asılılıqlar və lazım gəlir. Material asılılıqları formasına fiziki məhdudiyyətlər termodinamikanın ikinci qanunu-nun bütün şərtlərdə təmin edilməsi tələbi ilə tətbiq edilə bilər. Bərk cisimlərin bütöv mühit mexanikasında, əgər entropiya bərabərsizliyi şəklində təmin edilmişdirsə, termodinamikanın ikinci qanunu təmin edilmiş hesab olunur.
Müvazinət qanunları vahid həcmdə bir kəmiyyətin (kütlə, moment, enerji) dəyişmə tezliyinin üç səbəbdən yaranması ideyasını ifadə edir:
- fiziki kəmiyyət özlüyündə həcmi hüdudlandıran (sərhədləndirən) səthindən axır,
- həcmin səthində fiziki kəmiyyətin qaynağı (mənbəyi) mövcuddur, yaxud/və,
- həcm daxilində fiziki kəmiyyətin qaynağı vardır.
Gəlin, 


Cisim daxilindəki material nöqtələri aşağıdakı tənliklə deformasiya olunur
burada, 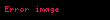
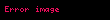
Deformasiya qradiyenti verilir
Müvazinət qanunları
Qoy 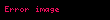
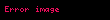

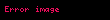



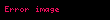

Onda, müvazinət qanunları aşağıdakı ümumi formada ifadə edilə bilər
Nəzər alın ki, 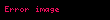
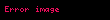

Əgər biz nöqteyi nəzərdən çıxış etsək, kütlə, moment, bucaq momenti və enerji üçün müvazinət qanunlarının aşağıdakı şəkildə olacağını göstərmək olar (kütlə və bucaq momenti üçün qaynaq həddlərin sıfır olduğu fərz olunur)
Yuxarıdakı bərabərliklərdə 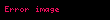
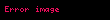



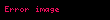



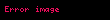



İstinad konfiqurasiyasına (Laqranj nöqteyi nəzərdən) nəzərən, müvazinət qanunları aşağıdakı kimi yazıla bilər
Yuxarıda, 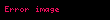

Biz əlavə olaraq birinci Piola-Kirxhof gərginlik tenzorunun transponiri olan nominal gərginlik tenzoru 
Beləliklə müvazinət qanunları aşağıdakı kimi də verilə bilər
Yuxarıdakı tənliklərdəki operatorlar belə təyin edilmişdir
harada 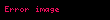

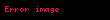
harada 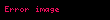


İkinci tərtib tenzorların daxili hasili (skalyar hasili) belə təyin edilmişdir
Klausius-Duhem bərabərsizliyi
Klausius-Duhem bərabərsizliyi elastik-plastik materiallarda termodinamikanın ikinci qanununu ifadə etmək üçün istifadə edilir. Bu bərabərsizlik təbii prosesslərin dönməzliyini, xüsusilə enerji itgisini, xarakterizə edən bir ifadədir.
Əvvəlki bölmədəki müvazinət tənliklərində olduğu kimi, nəzərdə tutulan bir kəmiyyətin selinin və mənbəsinin və eləcə də həmin kəmiyyətin vahid kütlədə daxili sıxlığının olması fərz edilir. Bu bölmədə nəzərdə tutulan kəmiyyət entropiyadır. Beləliklə, biz entropiya selinin, entropiya mənbəsinin və daxili spesifik entropiya (vahid kütləyə düşən entropiya) 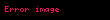


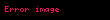


Gəlin 
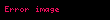

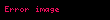

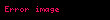
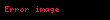
Skalyar entropiya seli, səthdəki vektoriyal sel ilə 
yuxarıda 

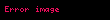

Beləliklə Klausius-Duhem bərabərsizliyi integral şəkildə verilir:
Biz göstərə bilərik ki, entropiya bərabərsizliyi differensial formada aşağıdakı kimi verilir
Koşi stressi və daxili enerjidən istifadə etməklə Klausius-Duhem bərabərsizliyi aşağıdakı kimi yazıla bilər
Qeydlər
Mənbələr
- Batra, R. C. Elements of Continuum Mechanics. Reston, VA: AIAA. 2006.
- Chandramouli, P.N. . Yes Dee Publishing Pvt Ltd. 2014. ISBN . 2018-08-04 tarixində orijinalından arxivləşdirilib. İstifadə tarixi: 2015-03-27.
- Eringen, A. Cemal. Mechanics of Continua (2nd edition). Krieger Pub Co. 1980. ISBN .
- Chen, Youping. Meshless Methods in Solid Mechanics (First Edition). Springer New York. 2009. ISBN .
- Dill, Ellis Harold. Continuum Mechanics: Elasticity, Plasticity, Viscoelasticity. Germany: CRC Press. 2006. ISBN .
- Dimitrienko, Yuriy. Nonlinear Continuum Mechanics and Large Inelastic Deformations. Germany: Springer. 2011. ISBN .
- Hutter, Kolumban; Klaus Jöhnk. Continuum Methods of Physical Modeling. Germany: Springer. 2004. ISBN .
- Fung, Y. C. A First Course in Continuum Mechanics (2nd). Prentice-Hall, Inc. 1977. ISBN .
- Gurtin, M. E. An Introduction to Continuum Mechanics. New York: Academic Press. 1981.
- Lai, W. Michael; David Rubin; Erhard Krempl. (3rd edition). Elsevier, Inc. 1996. ISBN . 2009-02-06 tarixində orijinalından arxivləşdirilib. İstifadə tarixi: 2015-03-27.
- Lubarda, Vlado A. Elastoplasticity Theory. CRC Press. 2001. ISBN .
- Lubliner, Jacob. (PDF). Dover Publications. 2008. ISBN . 2010-03-31 tarixində orijinalından (PDF) arxivləşdirilib. İstifadə tarixi: 2015-03-27.
- Malvern, Lawrence E. Introduction to the mechanics of a continuous medium. New Jersey: Prentice-Hall, Inc. 1969.
- Mase, George E. Continuum Mechanics. McGraw-Hill Professional. 1970. ISBN .
- Mase, G. Thomas; George E. Mase. Continuum Mechanics for Engineers (Second Edition). CRC Press. 1999. ISBN .
- Maugin, G. A. The Thermomechanics of Nonlinear Irreversible Behaviors: An Introduction. Singapore: World Scientific. 1999.
- Nemat-Nasser, Sia. Plasticity: A Treatise on Finite Deformation of Heterogeneous Inelastic Materials. Cambridge: Cambridge University Press. 2006. ISBN .
- Ostoja-Starzewski, Martin. Microstructural Randomness and Scaling in Mechanics of Materials. Boca Raton, FL: Chapman & Hall/CRC Press. 2008. ISBN .
- Rees, David. Basic Engineering Plasticity - An Introduction with Engineering and Manufacturing Applications. Butterworth-Heinemann. 2006. ISBN .
- Wright, T. W. The Physics and Mathematics of Adiabatic Shear Bands. Cambridge, UK: Cambridge University Press. 2002.
Xarici link
- www.continuummechanics.org
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Butov muhit mexanikasi mexanikanin bir bolmesi olub materiallarin mexaniki xassesini ve kinematik analizini oyrenir Materiallar diskret paylanmis hissecikler seklinde yox butov arasikesilmez paylanmis kutle seklinde modellesdirilir Bele bir model ilk defe XIX esrde Fransiz riyaziyyatcisi Auqusto Kosi fr Augustin Louis Cauchy terefinden ifade edilmisdir amma tedqiqatlar bu gun de davam etdirilir Butov muhit mexanikasiDiaqram Bernulli qanunundan istifade etmekle bir cixarisi gosterirQanunlar Elastiklik Plastiklik Huk qanunu Ozluluk Tezyiq Sarl qanunu Reologiya FerromayelerAlimlerBernoulli Boyl Kosi Sarl Eyler Huk Paskal NyutonbaxredakteQisa serhKlassik mexanikaF ddt mv displaystyle vec F frac mathrm d mathrm d t m vec v Nyutonun ikinci qanunuFundamental anlayislar Zaman Kutle Enerji ImpulsIfadelerNyuton mexanikasi BolmeleriButov muhit mexanikasiAlimlerQalileo Qaliley Iohan Kepler Isaak Nyuton Leonard Eyler Pyer Simon Laplas Jan Leron Dalamber Jozef Lui Laqranj Vilyam Hamilton Auqusto Kosibaxredakte Bir obyektin butov cisim seklinde modellesdirilmesi dedikde obyekti teskil eden cismin obyektin tutdugu fezani tamamile doldurmasi ferziyyesi nezerde tutulur Obyektin bele modellesdirilmesi maddenin atomlardan teskil olunmasini ve belelikle butov olmamasini nezere almir Buna baxmayaraq atomlar arasi mesafelerden qat qat boyuk olcu miqyaslarinda bele modeller olduqca deqiqdir Bele obyektlerin xassesini tesvir eden cixarilmasi ucun ve kimi ozul fizika qanunlarini bele modellere tetbiq etmek olar Butov muhit mexanikasi berk maye ve qazlarin fiziki xasselerini onlarin musahide edildiyi istenilen xususi koordinat sisteminden asili olmadan oyrenir Belelikle bu fiziki xasseler tenzorlarla ifade edilir ki tenzorlar teleb olunan xasseye malik riyazi predmet olub koordinat sisteminden asili deyildir Bu tenzorlar hesablamani asanlasdirmaq ucun koordinat sistemleri ile de ifade oluna biler AnlayisBerk maye ve qazlar kimi materiallar bos feza ile bir birinden ayrilmis molekullardan teskil olunub Mikroskopik olcude materiallarda catlar ve kesilmeler materialin butov ve davamli olmamasi onlarda qusurlarin olmasi nezerde tutulur movcuddur Buna baxmayaraq mueyyen fiziki hadiseler butov muhit cisimdeki madde miqdari kesilmez yayilmisdir ve cismin tutdugu fezani tamamile doldurur demekdir ferziyyesi qebul olunmaqla modellesdirile biler Bir butov muhit ele bir cisimdir ki o davamli olaraq cox kicik elementlere bolundukde bele bu kicik hissecikler esas cismin xasselerini ozunde saxlayir Butov muhit mexanikasinin esas saheleriButov muhit mexanikasi Butov kesilmez materiallarin fizikasini oyrenen elm Mueyyen olunmus dayaniqli formaya malik butov materiallarin fizikasini oyrenen elm Elastiklik Tetbiq olunmus gerginlikler goturuldukden sonra materialin dayaniqli veziyyetine qayitmasini tesvir edir Plastiklik Kifayet hedde quvve tetbiq edildikde qaliq deformasiyaya ugrayan materiallari tesvir edir Reologiya Berk ve maye xususiyyetine malik materiallari oyrenen elm Quvve tetbiq olunduqda formasini deyisen butov materiallarin fizikasini oyrenen elm tetbiq olunmus kesici gerginliye mutenasib olaraq nisbi deformasiya tezliyine meruz qalmir tetbiq olunmus kesici gerginliye mutenasib olaraq nisbi deformasiya tezliyine meruz qalir Modelin ifade olunmasiSekil 1 Butov cismin konfiqurasiyasi Butov muhit mexanikasi modeli modellesdirilecek material cisim B displaystyle mathcal B nin uc olculu mueyyen bir sahede yerlesdirilmesi ile baslanir Hemin sahedeki noqteler hissecikler ve ya material noqteleri adlandirilir Deformasiyaya ugrayan cisim Evklid fezasinda ilkin yerlesme sahesinden yerini deyismeye baslayir Deformasiyanin her aninda cismin fezada tutdugu her bir sahe bu cismin konfiqurasiyasi ve ya hali adlandirilir t displaystyle t zamaninda cismin konfiqurasiyasina uygun sahe kt B displaystyle kappa t mathcal B ile isarelenir Cisim daxilindeki her hansi bir hisseciyin mueyyen bir konfiqurasiyada veziyyeti radius vektoru ile ifade edilir x i 13xiei displaystyle mathbf x sum i 1 3 x i mathbf e i Burada ei displaystyle mathbf e i hell olunacaq mesele ucun teyin olunmus hesablama sisteminde Bax sekil 1 Bu vektor eyni zamanda hemin hisseciyin her hansi bir secilmis istinad konfiqurasiyasinda adeten cismin deformasiya olunmamis ilkin yerlesme konfiqurasiyasi istinad ve ya hereketin ve ya processin baslangic konfiqurasiyasi kimi secilir veziyyeti koordinantlari X displaystyle mathbf X in funksiyasi kimi ifade edile biler bele ki x kt X displaystyle mathbf x kappa t mathbf X Bu funksiya fiziki mena vermesi ucun muxtelif xassellere malik olmalidir kt displaystyle kappa t cdot zamanda kesilmezdir yeni cisimin deyismesi realligi eks edirir istenilen butun zaman kesiyinde ters funksiyasina malikdir yeni cisimde hec bir hissecik yox olmur ve ya yenisi yaranmir riyazi olaraq bu hisseciklerin deformasiya olunmus ve deformasiya olunmamis konfiqurasiyalarda birin bire elaqelerinin olmasini nezerde tutur deyismez oriyentasiyalidir yeni tebietde hec bir tansformasiya cisimde guzgu eksi yaratmir Modelin riyazi ifadesi ucun kt displaystyle kappa t cdot nin iki defe kesilmez differensiallanan olmasi ferz olunur bununla da cismin hereketini teyin eden differensial tenlikler ifade oluna biler Butov muhitde quvvelerButov muhit mexanikasi mutleq berk cisminlerin eksine deformasiya olunan cisimlerle mesguldur Berk cisim deformasiya oluna bilen cisim olub kesici muqavimete yeni kesici quvvelere cismin sethine parallel tesir gosteren quvve nezerde tutulur qarsi muqavimete malikdir Anacaq mayeler bele muqavimete malik deyiller Maye ve berk cisimleri tedqiq etmek ucun onlarin butov olmasi ferz olunur yeni onlarin hecimlerinin tutduqlari fezanin butun sahesini doldurmasi nezerde tutulur Ona gore de butov muhit mexanikasinda cisimdeki noqte ve ya hissecikden danisildiqda bu her hansi bir atom hisseciyi ve ya atom miqyasinda bir noqte deyil bu noqteni ehate eden cismin ideallasdirilmis bir hissesi nezerde tutulur Nyuton ve Eyler in klassik dinamikasina esaslanaraq bir maddi cismin hereketi ona tedbiq olunmus xarici quvvelerin tesirinden yaranir Bu quvvelerin iki cur sethi quvveler FC displaystyle mathbf F C ve hecmi quvveler FB displaystyle mathbf F B olmasi ferz olunur Belelikle cisime ve ya onun bir hissesine tedbiq edilmis yekun quvve F displaystyle mathcal F bele ifade oluna biler F FB FC displaystyle mathcal F mathbf F B mathbf F C Sethi quvveler ve ya temas quvveleri vahid saheye dusen quvve kimi ifade olunur Bu quvveler ya bir cismin basqa cisimlerle temasi neticesinde onun serhed sethine ya da bir cismin hisseleri arasindaki mexaniki qarsiliqli tesiri neticesine tesir sethinin her iki terefine tesir gostere biler Bir cisme xarici temas quvveleri tesir etdikde bu zaman daxili temas quvvelleri Nyutonun ucuncu hereket qanuna ve elecede bucaq momentinin ve xetli momentin saxlanmasi qanunlarina gore cisim daxilinde noqteden noqteye oturulmekle muvazinetlesir butov muhit mexanikasinda bu qanunlar Eylerin hereket qanunlari adlandirilir Daxili temas quvveleri material tenlikleri materialin fiziki xarakteristikasini mes elatiklik plastiklik ve s teyin eden tenlikler vasitesile cismin deformasiyasi ile elaqelendirilir Daxili quvvelerin cismin butun hecminde kesilmez olaraq yayilmasi ferz edilir Belelikle daxili quvveler temas quvve sixligi ve ya Kosi dartma sahesi T n x t displaystyle mathbf T mathbf n mathbf x t ile ifade edile biler Kosi dartma sahesi T n x t displaystyle mathbf T mathbf n mathbf x t daxili quvvelerin yayilmasini mueyyen bir konfiqurasiya ucun mueyyen bir t displaystyle t zamaninda temsil edir Bu sahe ancaq material noqtesinin yeri x displaystyle mathbf x den asili deyil eyni zamanda seth elementinin yerli lokal oriyentasiyasi n displaystyle mathbf n den yerli oriyentasiya T n x t displaystyle mathbf T mathbf n mathbf x t sahesinin x displaystyle mathbf x deki oriyentasiyasini bildirir de asilidir Ona gore de bu sahe vektor sahesi deyildir Verilmims bir daxili S displaystyle S sethinin her hansi n displaystyle mathbf n normal vektoruna malik differensial dS displaystyle dS sahesi differensial dFC displaystyle d mathbf F C temas quvvesine meruz qalir Bu quvve cismin S displaystyle S sethinin her iki terefindeki hisseleri arasindaki temasinin neticesinden yaranir ve bele ifade olunur dFC T n dS displaystyle d mathbf F C mathbf T mathbf n dS Burada T n displaystyle mathbf T mathbf n sethi dartqi ve ya gerginlik vektoru dartqi ve ya dartma vektoru adlandirilir Gerginlik vektoru koordinat sisteminin deyismesine nezeren invariantdir Xususi sethdeki yekun temas quvvesi S displaystyle S butun differensial sethlerdeki dS displaystyle dS temas quvvelerinin cemi kimi ifade edilir FC ST n dS displaystyle mathbf F C int S mathbf T mathbf n dS Butov muhit mexanikasinda bir cisim o halda gerginliksiz hesab edilir ki yegane movcud quvveller atomlar arasi ionik metalik ve Van der Vaals quvvelerdir ki bu quvveler de butun xarici tesirlerin yerin cazibe quvvesi de bura daxildir yoxlugunda cismin ozunu saxlamasi ve formasini qorumasi ucun vacibdir Cismin istehsali zamani yaranan gerginlikler de hesablanma zamani istisna edilir Belelikle butov muhit mexanikasinda gerginlikler adeten qebul olunmus ilkin konfiqurasiyaya nezeren deformasiyanin yaratdigi gerginlikleri nezerde tutur Basqa sozle cisimdeki gerginliyin mutleq gercek qiymetine deyil yalniz gerginlikdeki nisbi deyismelere baxilir Hecmi quvveler cismin hecmine ve ya kutlesine xaricden tesir gosteren quvvelerdir Hecmi quvvelerin xaricden tesir eden quvveler oldugunu demekle biz ferz edirik ki cismin muxtelif hisseleri arasindaki qarsiliqli tesir daxili quvveler yalniz temas kontakt quvveleri ile verilir Hecmi quvveler cismin mes qravitasiya sahesi elektrik sahesi ve ya maqnit sahesi kimi quvve sahelerinde yerlesmesinden yaranir Butov cismin kutlesinin kesilmez paylandigi ferz edildiyinden bu kutleden qaynaqlanan istenilen quvve de kesilmez paylanacaqdir Belelikle hecmi quvveler cismin butun hecmi uzre kesilmez olan yeni cismin her bir noqtesine tesir eden vektor saheleri ile verilir Hecmi quvveler hecmi quvve sixligi vahid kutleye dusen quvve b x t displaystyle mathbf b mathbf x t ile tesvir edilir Bu quvveler koordinant sisteminin secilmesinden asili deyildir Hecmi quvveler qravitasiya quvveleri olduqda bu quvvenin intensivliyi materialin kutle sixligi r x t displaystyle mathbf rho mathbf x t ile duz mutenasib olur ve vahid kutleye dusen quvve bi displaystyle b i yaxud vahid hecme dusen quvve pi displaystyle p i seklinde verile biler Bu iki kemiyyet bir biri ile materialin sixligi ile elaqelendirilir yeni rbi pi displaystyle rho b i p i Oxsar olaraq elektrik quvvelerinin intensivliyi elektrik yukunun miqdarindan asilidir Bir butov cisme tesir gosteren butun hecmi quvveler bele tesvir edilir FB Vbdm VrbdV displaystyle mathbf F B int V mathbf b dm int V rho mathbf b dV Cisme tesir gosteren hecmi quvveler ve temas quvveleri mueyyen bir noqteye nezeren muvafiq quvve momentleri firladici momentler yaradir Belelikle butun tetbiq olunmus firladici moment M displaystyle mathcal M koordiant baslangicina gore bele ifade edilir M MC MB displaystyle mathcal M mathbf M C mathbf M B Kinematika hereket ve deformasiyaSekil 2 Butov cismin hereketi Sekilde undeformed configuration deformasiya olunmamis konfiqurasiya deformed configuration deformasiya olunmus konfiqurasiya path line trayektoriya demekdir Butov cismin konfiqurasiyasinin deyismesi sahesi ile tesvir edilir Cismin yerdeyismesinin iki terkib hissesi movcuddur mutleq cisim yerdeyismesi ve deformasiya Mutleq cisim yerdeyismesi cismin forma ve olculerini deyismeyen eyni anda bas veren irelilleme ve firlanma hereketlerinden teskil olunur Deformasiya cismin baslangic veziyyetine nezeren forma ve ya olculerini deyismesini bildirir Cismin baslangic veziyyeti onun baslangic ve ya istinad konfiqurasiyasi k0 B displaystyle kappa 0 mathcal B ve deformasiya olunmus veziyyeti ise onun cari ve ya deformasiya olunmus konfiqurasiyasi kt B displaystyle kappa t mathcal B adlanir Sekil 2 Butov bir cismin hereketi yerdeyismelerin zamanda kesilmez ardicilligindan ibaretdir Belelikle material cisim muxtelif zaman anlarinda muxtelif konfiqurasiyalari tutur ki cismin istenilen bir hisseciyi de fezada uygun olaraq mueyyen noqteler sirasininda yerini deyisir Bu noqteler sirasi hemin hisseciyin trayektoriyasini tesvir edir Butov cisimin deformasiyasi ve ya hereketi erzinde asagidaki menada kesilmezlik vardir Istenilen bir zaman aninda qapali bir eyri meydana getiren material noqteleri sonraki istenilen zaman ardicilligina da hemise qapali bir eyri meydana getirecekler Istenilen bir zaman aninda qapali bir seth meydana getiren material noqteleri sonraki istenilen zaman ardicilliginda da hemise qapali bir seth meydana getirecekler ve bu qapali seth daxilindeki madde hemise bu seth daxilinde qalacaqdir Esas tenliklerButov muhit mexanikasi materiallarin xasseleri ile mesgul olur ki onlar mueyyen uzunluq ve zaman miqyaslari ucun kesilmez olaraq teqribi hesablana biler Materiallarin mexanikasini teyin eden bele tenliklere ve ucun muvazinet balans ve ya saxlanma qanunlari daxildir Esas idareedici tenlikler sistemini tamlamaq ucun asililiqlar ve lazim gelir Material asililiqlari formasina fiziki mehdudiyyetler termodinamikanin ikinci qanunu nun butun sertlerde temin edilmesi telebi ile tetbiq edile biler Berk cisimlerin butov muhit mexanikasinda eger entropiya berabersizliyi seklinde temin edilmisdirse termodinamikanin ikinci qanunu temin edilmis hesab olunur Muvazinet qanunlari vahid hecmde bir kemiyyetin kutle moment enerji deyisme tezliyinin uc sebebden yaranmasi ideyasini ifade edir fiziki kemiyyet ozluyunde hecmi hududlandiran serhedlendiren sethinden axir hecmin sethinde fiziki kemiyyetin qaynagi menbeyi movcuddur yaxud ve hecm daxilinde fiziki kemiyyetin qaynagi vardir Gelin W displaystyle Omega ile cisimi Evkilid fezasinda bir aciq altcoxluq ve W displaystyle partial Omega ile ise onun sethini W displaystyle Omega nin serheddi gosterek Cisim daxilindeki material noqteleri asagidaki tenlikle deformasiya olunur x x X x X displaystyle mathbf x boldsymbol chi mathbf X mathbf x mathbf X burada X displaystyle mathbf X baslangic konfiqurasiyada her hansi bir noqtenin veziyyetini yerini ve x displaystyle mathbf x ise deformasiya olunmus konfiqurasiyada noqtenin yerini gosterir Deformasiya qradiyenti verilir F x X x displaystyle boldsymbol F frac partial mathbf x partial mathbf X nabla boldsymbol mathbf x Muvazinet qanunlari Qoy f x t displaystyle f mathbf x t cisim daxilinde axaran her hansi bir fiziki kemiyyet olsun Elece de gelin g x t displaystyle g mathbf x t le cismin sethindeki qanaqlari h x t displaystyle h mathbf x t le ise daxilindeki qaynaqlari isareleyek Gelin n x t displaystyle mathbf n mathbf x t in cismin W displaystyle partial Omega sethinin vahid normalini isarelemesini qebul edek v x t displaystyle mathbf v mathbf x t ise axan fiziki kemiyyeti ozleri ile dasiyan fiziki hisseciklerin axin suretini nezerde tutur Eyni W displaystyle partial Omega hereket sureti un displaystyle u n n displaystyle mathbf n istiqametinde isarelenir Onda muvazinet qanunlari asagidaki umumi formada ifade edile biler ddt Wf x t dV Wf x t un x t v x t n x t dA Wg x t dA Wh x t dV displaystyle cfrac d dt left int Omega f mathbf x t text dV right int partial Omega f mathbf x t u n mathbf x t mathbf v mathbf x t cdot mathbf n mathbf x t text dA int partial Omega g mathbf x t text dA int Omega h mathbf x t text dV Nezer alin ki f x t displaystyle f mathbf x t g x t displaystyle g mathbf x t ve h x t displaystyle h mathbf x t funksiyalari skalyar vektorial ve ya tenzorial qiymetli funksiyalar ola biler ki bu da muvazinet qanununa daxil olan fiziki kemiyyetden asilidir Eger cisimde daxili serhedler sicrayisli kesilmeler olarsa onlar da muvazinet qanunlarinda nezerde tutulmalidir Eger biz noqteyi nezerden cixis etsek kutle moment bucaq momenti ve enerji ucun muvazinet qanunlarinin asagidaki sekilde olacagini gostermek olar kutle ve bucaq momenti ucun qaynaq heddlerin sifir oldugu ferz olunur r r v 0Kutlenin muvazineti saxlanmasi r v s r b 0Xetli momentin muvazineti Kosinin birinci hereket qanunu s sTBucaq momentinin muvazineti Kosinin ikinci hereket qanunu r e s v q r s 0Enerjinin muvazineti displaystyle begin aligned dot rho rho boldsymbol nabla cdot mathbf v amp 0 amp amp qquad text Kutlenin muvazineti saxlanmasi rho dot mathbf v boldsymbol nabla cdot boldsymbol sigma rho mathbf b amp 0 amp amp qquad text Xetli momentin muvazineti Kosinin birinci hereket qanunu boldsymbol sigma amp boldsymbol sigma T amp amp qquad text Bucaq momentinin muvazineti Kosinin ikinci hereket qanunu rho dot e boldsymbol sigma boldsymbol nabla mathbf v boldsymbol nabla cdot mathbf q rho s amp 0 amp amp qquad text Enerjinin muvazineti end aligned Yuxaridaki beraberliklerde r x t displaystyle rho mathbf x t kutle sixligi cari r displaystyle dot rho r displaystyle rho nun material zaman toremesi v x t displaystyle mathbf v mathbf x t hisseciyin sureti v displaystyle dot mathbf v v displaystyle mathbf v nin material zaman toremesi s x t displaystyle boldsymbol sigma mathbf x t b x t displaystyle mathbf b mathbf x t hecmi quvve sixligi e x t displaystyle e mathbf x t vahid kutleye dusen daxili enerji e displaystyle dot e e displaystyle e nin material zaman toremesi q x t displaystyle mathbf q mathbf x t istilik seli vektoru ve s x t displaystyle s mathbf x t vahid kutleye dusen enerji qaynagidir Istinad konfiqurasiyasina Laqranj noqteyi nezerden nezeren muvazinet qanunlari asagidaki kimi yazila biler r det F r0 0Kutlenin muvazineti saxlanmasi r0 x PT r0 b 0Xetli momentin muvazinetiF PT P FTBucaq momentinin muvazinetir0 e PT F q r0 s 0Enerjinin muvazineti displaystyle begin aligned rho det boldsymbol F rho 0 amp 0 amp amp qquad text Kutlenin muvazineti saxlanmasi rho 0 ddot mathbf x boldsymbol nabla circ cdot boldsymbol P T rho 0 mathbf b amp 0 amp amp qquad text Xetli momentin muvazineti boldsymbol F cdot boldsymbol P T amp boldsymbol P cdot boldsymbol F T amp amp qquad text Bucaq momentinin muvazineti rho 0 dot e boldsymbol P T dot boldsymbol F boldsymbol nabla circ cdot mathbf q rho 0 s amp 0 amp amp qquad text Enerjinin muvazineti end aligned Yuxarida P displaystyle boldsymbol P birinci r0 displaystyle rho 0 ise istinad konfiqurasiyasinda kutle sixligidir Birinci Piola Kirxhof gerginlik tenzoru ile Kosi gerginlik tenzoru arasinda asagidaki asgidaki elaqe movcuddur P J s F T where J det F displaystyle boldsymbol P J boldsymbol sigma cdot boldsymbol F T text where J det boldsymbol F Biz elave olaraq birinci Piola Kirxhof gerginlik tenzorunun transponiri olan nominal gerginlik tenzoru N displaystyle boldsymbol N i teyin edirik N PT J F 1 s displaystyle boldsymbol N boldsymbol P T J boldsymbol F 1 cdot boldsymbol sigma Belelikle muvazinet qanunlari asagidaki kimi de verile biler r det F r0 0Kutlenin muvazineti saxlanmasi r0 x N r0 b 0Xetli momentin muvazinetiF N NT FTBucaq momentinin muvazinetir0 e N F q r0 s 0Enerjinin muvazineti displaystyle begin aligned rho det boldsymbol F rho 0 amp 0 amp amp qquad text Kutlenin muvazineti saxlanmasi rho 0 ddot mathbf x boldsymbol nabla circ cdot boldsymbol N rho 0 mathbf b amp 0 amp amp qquad text Xetli momentin muvazineti boldsymbol F cdot boldsymbol N amp boldsymbol N T cdot boldsymbol F T amp amp qquad text Bucaq momentinin muvazineti rho 0 dot e boldsymbol N dot boldsymbol F boldsymbol nabla circ cdot mathbf q rho 0 s amp 0 amp amp qquad text Enerjinin muvazineti end aligned Yuxaridaki tenliklerdeki operatorlar bele teyin edilmisdir v i j 13 vi xjei ej vi jei ej v i 13 vi xi vi i S i j 13 Sij xj ei sij j ei displaystyle boldsymbol nabla mathbf v sum i j 1 3 frac partial v i partial x j mathbf e i otimes mathbf e j v i j mathbf e i otimes mathbf e j boldsymbol nabla cdot mathbf v sum i 1 3 frac partial v i partial x i v i i boldsymbol nabla cdot boldsymbol S sum i j 1 3 frac partial S ij partial x j mathbf e i sigma ij j mathbf e i harada v displaystyle mathbf v bir vektor sahesini S displaystyle boldsymbol S bir ikinci tertib tenzor sahesini ve ei displaystyle mathbf e i ise cari konfiqurasiyada ortonormal bazisin komponentleridir Eyni ile v i j 13 vi XjEi Ej vi jEi Ej v i 13 vi Xi vi i S i j 13 Sij Xj Ei Sij j Ei displaystyle boldsymbol nabla circ mathbf v sum i j 1 3 frac partial v i partial X j mathbf E i otimes mathbf E j v i j mathbf E i otimes mathbf E j boldsymbol nabla circ cdot mathbf v sum i 1 3 frac partial v i partial X i v i i boldsymbol nabla circ cdot boldsymbol S sum i j 1 3 frac partial S ij partial X j mathbf E i S ij j mathbf E i harada v displaystyle mathbf v bir vektor sahesini S displaystyle boldsymbol S bir ikinci etrtib tenzor sahesini ve Ei displaystyle mathbf E i ise istinad konfiqurasiyada ortonormal bazisin komponentleridir Ikinci tertib tenzorlarin daxili hasili skalyar hasili bele teyin edilmisdir A B i j 13Aij Bij trace ABT displaystyle boldsymbol A boldsymbol B sum i j 1 3 A ij B ij operatorname trace boldsymbol A boldsymbol B T Klausius Duhem berabersizliyi Klausius Duhem berabersizliyi elastik plastik materiallarda termodinamikanin ikinci qanununu ifade etmek ucun istifade edilir Bu berabersizlik tebii prosesslerin donmezliyini xususile enerji itgisini xarakterize eden bir ifadedir Evvelki bolmedeki muvazinet tenliklerinde oldugu kimi nezerde tutulan bir kemiyyetin selinin ve menbesinin ve elece de hemin kemiyyetin vahid kutlede daxili sixliginin olmasi ferz edilir Bu bolmede nezerde tutulan kemiyyet entropiyadir Belelikle biz entropiya selinin entropiya menbesinin ve daxili spesifik entropiya vahid kutleye dusen entropiya h displaystyle eta nin baxilan bolgede olmasini ferz edirik W displaystyle Omega ile bele bir bolgeni ve W displaystyle partial Omega ile onun serhedini isareleyek Bu zaman termodinamikanin ikinci qanunu ifade edir ki h displaystyle eta nin bu bolege artma tezliyi daxili entropiya sixliginin rh displaystyle rho eta deyismesi ile entropiyanin W displaystyle Omega ya sel ve yaxud daxili menbeler vasitesile techizinin ceminden boyuk yaxud beraberdir Daxili entropiya sixliginin deyismesi baxilan bolgeye materialin axaraq daxil ve xaric olmasi ile elaqelendirilir Gelin W displaystyle partial Omega nun un displaystyle u n axis sureti ile hereketde olmasini ve W displaystyle Omega daxilindeki hisseciklerin v displaystyle mathbf v suretlerine malik olmasini ferz edek r displaystyle rho ise bolgede maddenin sixligini q displaystyle bar q sethde entropiya selini ve r displaystyle r vahid hecme dusen entropiya menbeyini gostersin Belelikle entropiya berabersizliyi asagidaki kimi yazila biler ddt Wr h dV Wr h un v n dA Wq dA Wr r dV displaystyle cfrac d dt left int Omega rho eta text dV right geq int partial Omega rho eta u n mathbf v cdot mathbf n text dA int partial Omega bar q text dA int Omega rho r text dV Skalyar entropiya seli sethdeki vektoriyal sel ile q ps x n displaystyle bar q boldsymbol psi mathbf x cdot mathbf n ifadesi vasitesile elaqelendirle biler Zamanin her kicik artan ani ucun isotermal sertler ferz edildikde biz yaza bilerik ps x q x T r sT displaystyle boldsymbol psi mathbf x cfrac mathbf q mathbf x T r cfrac s T yuxarida q displaystyle mathbf q istilik seli vektoru s displaystyle s vahid hecme dusen enerji menbeyi T displaystyle T ise mutleq temperaturdur Kemiyyetler her hansi bir material noqtenin x displaystyle mathbf x veziyyetine ve t displaystyle t zamanina uygun gelir Belelikle Klausius Duhem berabersizliyi integral sekilde verilir ddt Wr h dV Wr h un v n dA Wq nT dA Wr sT dV displaystyle cfrac d dt left int Omega rho eta text dV right geq int partial Omega rho eta u n mathbf v cdot mathbf n text dA int partial Omega cfrac mathbf q cdot mathbf n T text dA int Omega cfrac rho s T text dV Biz gostere bilerik ki entropiya berabersizliyi differensial formada asagidaki kimi verilir r h qT r sT displaystyle rho dot eta geq boldsymbol nabla cdot left cfrac mathbf q T right cfrac rho s T Kosi stressi ve daxili enerjiden istifade etmekle Klausius Duhem berabersizliyi asagidaki kimi yazila biler r e T h s v q TT displaystyle rho dot e T dot eta boldsymbol sigma boldsymbol nabla mathbf v leq cfrac mathbf q cdot boldsymbol nabla T T QeydlerSmith amp Truesdell p 97 Slaughter Lubliner Liu Wu Fung Mase Atanackovic Irgens Liu ChadwickMenbelerBatra R C Elements of Continuum Mechanics Reston VA AIAA 2006 Chandramouli P N Yes Dee Publishing Pvt Ltd 2014 ISBN 9789380381398 2018 08 04 tarixinde orijinalindan arxivlesdirilib Istifade tarixi 2015 03 27 Eringen A Cemal Mechanics of Continua 2nd edition Krieger Pub Co 1980 ISBN 0 88275 663 X Chen Youping Meshless Methods in Solid Mechanics First Edition Springer New York 2009 ISBN 1 4419 2148 6 Dill Ellis Harold Continuum Mechanics Elasticity Plasticity Viscoelasticity Germany CRC Press 2006 ISBN 0 8493 9779 0 Dimitrienko Yuriy Nonlinear Continuum Mechanics and Large Inelastic Deformations Germany Springer 2011 ISBN 978 94 007 0033 8 Hutter Kolumban Klaus Johnk Continuum Methods of Physical Modeling Germany Springer 2004 ISBN 3 540 20619 1 Fung Y C A First Course in Continuum Mechanics 2nd Prentice Hall Inc 1977 ISBN 0 13 318311 4 Gurtin M E An Introduction to Continuum Mechanics New York Academic Press 1981 Lai W Michael David Rubin Erhard Krempl 3rd edition Elsevier Inc 1996 ISBN 978 0 7506 2894 5 2009 02 06 tarixinde orijinalindan arxivlesdirilib Istifade tarixi 2015 03 27 Lubarda Vlado A Elastoplasticity Theory CRC Press 2001 ISBN 0 8493 1138 1 Lubliner Jacob PDF Dover Publications 2008 ISBN 0 486 46290 0 2010 03 31 tarixinde orijinalindan PDF arxivlesdirilib Istifade tarixi 2015 03 27 Malvern Lawrence E Introduction to the mechanics of a continuous medium New Jersey Prentice Hall Inc 1969 Mase George E Continuum Mechanics McGraw Hill Professional 1970 ISBN 0 07 040663 4 Mase G Thomas George E Mase Continuum Mechanics for Engineers Second Edition CRC Press 1999 ISBN 0 8493 1855 6 Maugin G A The Thermomechanics of Nonlinear Irreversible Behaviors An Introduction Singapore World Scientific 1999 Nemat Nasser Sia Plasticity A Treatise on Finite Deformation of Heterogeneous Inelastic Materials Cambridge Cambridge University Press 2006 ISBN 0 521 83979 3 Ostoja Starzewski Martin Microstructural Randomness and Scaling in Mechanics of Materials Boca Raton FL Chapman amp Hall CRC Press 2008 ISBN 978 1 58488 417 0 Rees David Basic Engineering Plasticity An Introduction with Engineering and Manufacturing Applications Butterworth Heinemann 2006 ISBN 0 7506 8025 3 Wright T W The Physics and Mathematics of Adiabatic Shear Bands Cambridge UK Cambridge University Press 2002 Xarici linkwww continuummechanics org
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State