Arximed aksiomu və ya Arximed prinsipi və ya Arximed mülkiyyəti — Qədim yunan riyaziyyatçısı Arximedin adını daşıyan riyazi ifadələr.

Bu təklif əvvəlcə Knidli Evdoks Kəmiyyətlər münasibətləri nəzəriyyəsində formalaşdırıldı (Evdoksun kəmiyyət anlayışı həm nömrələri, həm də davamlı kəmiyyətləri əhatə edir: parçalar, sahələr, həcmlər):
İki miqdar varsa və , -dən azdırsa, sonra olaraq götürüb,kifayət qədər -ni kənarlaşdıra bilərik:
Məsələn, seqmentlər üçün Arximed aksiomu belə səslənir: əgər iki seqment verilirsə, onlardan daha kiçik olanı kifayət qədər dəfə təxirə salmaqla daha böyük hissəni örtə bilər.
Arximed aksiomu ifadəsi mənasız görünür,lakin əsl mənası sonsuz və ya sonsuz böyük miqdarda olmamasıdır. Beləliklə, bu aksiom qeyri-standart analizdə yerinə yetirilmir: hiperreal ədədlər dəstində sonsuz və sonsuz böyük miqdarlar var. Bu cür elementlər Arximedin aksiomunu qane edə bilməz. Digər nümunələr mümkündür.
Arximed əmlakının razı olduğu riyazi quruluşlar,arximediya adlanır,məsələn, Arximed sahəsi və Arximed qrupu və yerinə yetirilməyənlər isə - arximediya deyil.
Tarixi
Riyaziyyatda Arximedin aksiomu kimi tanınan aksiom, əslində ilk olaraq Knidli Evdoks tərəfindən tərtib edilmişdir. Bu təklif əslində əsl ədədlərin ilk aksiomatik nəzəriyyəsi olan münasibətlər nəzəriyyəsində əsas rol oynadı. Buna görə də buna Evdoksun aksiomu da deyilir.
Evdoksun nəzəriyyəsi bizə Evklidin təqdimatında gəldi.("Başlanğıclar", Kitab V).
 | Kəmiyyətlərin bir-biri ilə əlaqəli olduğu deyilir,əgər onlar çoxaldılarsa onlar bir-birini üstələyə bilərlər. "Başlanğıclar",V Kitab,4-cü tərif |  |
Evdoksun aksiomu - Arximed, Evdoks tərəfindən icad edilən "tükənmə metodu" adını daşıyır -Rieman inteqralıvə Darb nəzəriyyəsi analoqundan istifadə etməklə rəqəmlərin sahələrini, bədən həcmlərini, qövslərin uzunluqlarını tapmaq üsuludur. Bununla birlikdə, Arximed bu sahədə ən böyük nəticələrə nail oldu. Öz metodundan istifadə edərək Evdoks sahələrin və həcmlərin hesablanmasına dair bir neçə teoremi ciddi şəkildə sübut etdi. Üstəlik, Qədim Yunanıstanda ardıcıllıq anlayışı olmadığından, ardıcıllığın həddi olduğu üçün Arximed hər konkret tapşırıqda arqumenti yenidən təkrarlamalı idi. Beləliklə, Arximed öz yazılarında Evdoksun - Arximedin aksiomlarını tərtib etmiş və istifadə etmişdir. Eyni zamanda, Arximed özü [en]kitabının giriş hissəsində bu aksiomun sələfləri tərəfindən istifadə edildiyini və Evdoksun əsərlərində əhəmiyyətli rol oynadığını vurğulayır..
Müasir tərif
Xətti sifarişli qrup
Qoy 















Sifarişli sahə
Qoy 
Qoy 

elementi
elementinə nisbətində sonsuz kiçikdir,yalnız onda
-yə münasibətdə sonsuz kiçik olur (belə elementlər sadəcə sonsuz kiçik adlanır).
elementi
elementinə nisbətən sonsuz dərəcədə böyükdür, yalnız onda
-yə münasibətdə sonsuz böyük olur (belə elementlər sadəcə sonsuz böyük adlanır).
Sonsuz kiçik və sonsuz böyük elementlər sonsuz elementlər adı altında birləşdirilir.
Müvafiq olaraq, Arximed aksiomunun tərtib edilməsi sadələşdirilir: sifariş edilmiş sahə 
Hər hansı 



Və ya, ekvivalent formula:
Sahənin hər hansı bir müsbət 


Nümunələr və əks misallar
Həqiqi ədədlər toplusu
Arximed sahəsinin ən məşhur nümunəsi həqiqi ədədlər toplusudur. Həqiqi ədədlər toplusunu rasional dəstin tamamlanması hesab etsək (məsələn, Dedekind kəsiyindən istifadə etməklə),onda həqiqi ədədlər üçün Arximed əmlakı rasional ədədlərin ona sahib olmasıdır.Bununla əlaqədar olaraq qeyd etmək lazımdır ki, David Hilbert tərəfindən təklif olunan həqiqi ədədlərin aksiomu sistemlərindən birində (Hilbertin aksiomatikası),həqiqi ədədlər toplusu, maksimum arximediya sifariş edilmiş sahə, yəni Arximed aksiomunu təmin edən sifarişli bir sahə olaraq təyin olunaraq (yəni sonsuz elementləri ehtiva etmir),daha böyük bir Arximediya sifariş edilmiş sahəyə genişləndirilə bilməz.
Arximed olmayan sifarişli sahə
Arximed aksiomunun yerinə yetirilmədiyi sifariş edilmiş bir sahənin nümunəsi (daha doğrusu, əks misal) olaraq, real əmsallar, yəni forma funksiyaları ilə rasional funksiyalar toplusunu nəzərdən keçiririk

Ümumi əlavə və vurma əməliyyatlarına gəlincə bu məcmu bir sahə meydana gətirir. Rasional funksiyaların cəminə sifarişin əlaqəsini aşağıdakı kimi təqdim edirik.








burada sağ tərəfdəki son müddət müntəzəm rasional fraksiyadır, yəni ədədi dərəcəsi məxrəc dərəcəsindən azdır: 

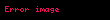

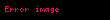

Beləliklə, rasional funksiyaların cəmi sifarişli bir sahə təşkil edir. Qeyd edək ki, bu həqiqi ədədlər sahəsinin uzantısıdır, lakin Arximedin aksiomu burada tətbiq edilmir(əvvəlki hissənin sonuna baxın!).Həqiqətən, 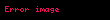



Başqa sözlə, 
Həmçinin bax
İstinadlar
- А. П. Юшкевича. История математики. Наука. 2003. səh. 96.
- Евклид. Начала. 1. М.—Л.: Главное Издательство Технико-Теоретической Литературы. 1948.
- Бурбаки, Н. Очерки по истории математики. М.: Издательство иностранной литературы. Пер. И. Г. Башмаковой под ред. К. А. Рыбникова. 1963. 148.
- Гильберт, Д. Основания геометрии. М.—Л.: Главное Издательство Технико-Теоретической Литературы. 1948. 87.
Ədəbiyyat
- История математики. 1. М.: «Наука». Под ред. А. П. Юшкевича. 2003.
- Евклид. Начала. 1. М.—Л.: Главное Издательство Технико-Теоретической Литературы. Перевод Д. Д. Мордухай—Болтовского. 1948.
- Гильберт, Д. Основания геометрии. М.—Л.: Главное Издательство Технико-Теоретической Литературы. 1948.
- Бурбаки, Н. Очерки по истории математики. М.: Издательство иностранной литературы. Пер. И. Г. Башмаковой под ред. К. А. Рыбникова. 1963.
Xarici keçidlər
- Archimède : fizika tarixi (isp.)
- Riyazi Analiz fənninin proqramı
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Arximed aksiomu ve ya Arximed prinsipi ve ya Arximed mulkiyyeti Qedim yunan riyaziyyatcisi Arximedin adini dasiyan riyazi ifadeler Seqmentler ucun Arximed aksiomu Bu teklif evvelce Knidli Evdoks Kemiyyetler munasibetleri nezeriyyesinde formalasdirildi Evdoksun kemiyyet anlayisi hem nomreleri hem de davamli kemiyyetleri ehate edir parcalar saheler hecmler Iki miqdar varsa a displaystyle a ve b displaystyle b a displaystyle a b displaystyle b den azdirsa sonra a displaystyle a olaraq goturub kifayet qeder b displaystyle b ni kenarlasdira bilerik a a a n gt b displaystyle underbrace a a ldots a n gt b Meselen seqmentler ucun Arximed aksiomu bele seslenir eger iki seqment verilirse onlardan daha kicik olani kifayet qeder defe texire salmaqla daha boyuk hisseni orte biler Arximed aksiomu ifadesi menasiz gorunur lakin esl menasi sonsuz ve ya sonsuz boyuk miqdarda olmamasidir Belelikle bu aksiom qeyri standart analizde yerine yetirilmir hiperreal ededler destinde sonsuz ve sonsuz boyuk miqdarlar var Bu cur elementler Arximedin aksiomunu qane ede bilmez Diger numuneler mumkundur Arximed emlakinin razi oldugu riyazi quruluslar arximediya adlanir meselen Arximed sahesi ve Arximed qrupu ve yerine yetirilmeyenler ise arximediya deyil TarixiRiyaziyyatda Arximedin aksiomu kimi taninan aksiom eslinde ilk olaraq Knidli Evdoks terefinden tertib edilmisdir Bu teklif eslinde esl ededlerin ilk aksiomatik nezeriyyesi olan munasibetler nezeriyyesinde esas rol oynadi Buna gore de buna Evdoksun aksiomu da deyilir Evdoksun nezeriyyesi bize Evklidin teqdimatinda geldi Baslangiclar Kitab V Kemiyyetlerin bir biri ile elaqeli oldugu deyilir eger onlar coxaldilarsa onlar bir birini usteleye bilerler Baslangiclar V Kitab 4 cu terif Evdoksun aksiomu Arximed Evdoks terefinden icad edilen tukenme metodu adini dasiyir Rieman inteqralive Darb nezeriyyesi analoqundan istifade etmekle reqemlerin sahelerini beden hecmlerini qovslerin uzunluqlarini tapmaq usuludur Bununla birlikde Arximed bu sahede en boyuk neticelere nail oldu Oz metodundan istifade ederek Evdoks sahelerin ve hecmlerin hesablanmasina dair bir nece teoremi ciddi sekilde subut etdi Ustelik Qedim Yunanistanda ardicilliq anlayisi olmadigindan ardicilligin heddi oldugu ucun Arximed her konkret tapsiriqda arqumenti yeniden tekrarlamali idi Belelikle Arximed oz yazilarinda Evdoksun Arximedin aksiomlarini tertib etmis ve istifade etmisdir Eyni zamanda Arximed ozu en kitabinin giris hissesinde bu aksiomun selefleri terefinden istifade edildiyini ve Evdoksun eserlerinde ehemiyyetli rol oynadigini vurgulayir Muasir terifXetti sifarisli qrup Qoy G displaystyle G xetti sifarisli qrup a displaystyle a ve b displaystyle b G displaystyle G in musbet elementleri olsun a displaystyle a elementi b displaystyle b elementine munasibetde sonsuz kicikdir lakin eger her hansi bir tebii n displaystyle n berabersizliyi varsa b displaystyle b a displaystyle a ya munasibetdesonsuz boyukdur a a a n lt b displaystyle underbrace a a ldots a n lt b G displaystyle G qrupu eger Arximedin aksiomu yerine yetirilirse Arximediya adlanir G displaystyle G de a displaystyle a elementleri cutu yoxdur bele ki b displaystyle b a displaystyle a b displaystyle b b displaystyle b ye munasibetde sonsuz kicikdir Sifarisli sahe Qoy K displaystyle K sifarisli bir sahe olsun Her sifaris edilmis sahe xetti sifaris edilmis bir qrup oldugundan onda sonsuz kicik ve sonsuz boyuk elementlerin yuxaridaki butun terifleri hemcinin Arximed aksiomunun tertib edilmesi quvvede qalir Bununla birlikde bir sira spesifik xususiyyetler movcuddur buna gore de Arximed aksiomunun formalasdirilmasi sadelesdirilmisdir Qoy a b displaystyle a b K displaystyle K nin musbet elementleri olsun a displaystyle a elementi b displaystyle b elementine nisbetinde sonsuz kicikdir yalniz onda a b displaystyle a b 1 K displaystyle 1 in K ye munasibetde sonsuz kicik olur bele elementler sadece sonsuz kicik adlanir a displaystyle a elementi b displaystyle b elementine nisbeten sonsuz derecede boyukdur yalniz onda a b displaystyle a b 1 K displaystyle 1 in K ye munasibetde sonsuz boyuk olur bele elementler sadece sonsuz boyuk adlanir Sonsuz kicik ve sonsuz boyuk elementler sonsuz elementler adi altinda birlesdirilir Muvafiq olaraq Arximed aksiomunun tertib edilmesi sadelesdirilir sifaris edilmis sahe K displaystyle K sonsuz kicik elementlere sahib deyilse ve ya eyni derecede sonsuz boyuk elementlere sahib deyilse Arximed mulkiyyetine malikdir Sonsuz kicik ve ya sonsuz boyuk bir elementin terifini burada genislendirsek Arximed aksiomunun asagidaki formulasini aliriq Her hansi a displaystyle a elementi K displaystyle K sahesi ucun tebii n displaystyle n n gt a displaystyle n gt a kimi elementleri movcuddur Ve ya ekvivalent formula Sahenin her hansi bir musbet e gt 0 displaystyle varepsilon gt 0 elementi ucun tebii n displaystyle n 1 n lt e displaystyle 1 n lt varepsilon kimi elementleri movcuddur Numuneler ve eks misallarHeqiqi ededler toplusu Arximed sahesinin en meshur numunesi heqiqi ededler toplusudur Heqiqi ededler toplusunu rasional destin tamamlanmasi hesab etsek meselen Dedekind kesiyinden istifade etmekle onda heqiqi ededler ucun Arximed emlaki rasional ededlerin ona sahib olmasidir Bununla elaqedar olaraq qeyd etmek lazimdir ki David Hilbert terefinden teklif olunan heqiqi ededlerin aksiomu sistemlerinden birinde Hilbertin aksiomatikasi heqiqi ededler toplusu maksimum arximediya sifaris edilmis sahe yeni Arximed aksiomunu temin eden sifarisli bir sahe olaraq teyin olunaraq yeni sonsuz elementleri ehtiva etmir daha boyuk bir Arximediya sifaris edilmis saheye genislendirile bilmez Arximed olmayan sifarisli sahe Arximed aksiomunun yerine yetirilmediyi sifaris edilmis bir sahenin numunesi daha dogrusu eks misal olaraq real emsallar yeni forma funksiyalari ile rasional funksiyalar toplusunu nezerden keciririk R x anxn a1x a0bmxm b1x b0 displaystyle R x frac a n x n ldots a 1 x a 0 b m x m ldots b 1 x b 0 Umumi elave ve vurma emeliyyatlarina gelince bu mecmu bir sahe meydana getirir Rasional funksiyalarin cemine sifarisin elaqesini asagidaki kimi teqdim edirik f displaystyle f ve g displaystyle g iki rasional funksiyadir Deyirik ki f gt g displaystyle f gt g eger bezi mehellelerde displaystyle infty ile ferq olduqda f g displaystyle f g ciddi bir musbet isareye malik olur Bu sert rasional funksiyalarin emsallarif displaystyle f ve g displaystyle g baximindan tertib edile biler Ferqi f g displaystyle f g coxbucaqli muntezem rasional fraksiya seklinde yaziriq f x g x cn mxn m c1x c0 dkxk d1x d0xm bm 1xm 1 b1x b0 displaystyle f x g x c n m x n m ldots c 1 x c 0 frac d k x k ldots d 1 x d 0 x m b m 1 x m 1 ldots b 1 x b 0 burada sag terefdeki son muddet muntezem rasional fraksiyadir yeni ededi derecesi mexrec derecesinden azdir k lt m displaystyle k lt m Biz de mexrecin en yuksek emsali bm displaystyle b m 1 displaystyle 1 oldugunu hesab edeceyik Sonra f gt g displaystyle f gt g olarsa yalniz onda her hansi cn m gt 0 displaystyle c n m gt 0 ya coxbucaqli hisse itir ve ya dk gt 0 displaystyle d k gt 0 olur Teqdim olunan qaydanin duzgunluyunu yoxlamaq asandir tetbiq olunan elaqenin heqiqeten sifaris elaqesi oldugunu ve bu elaqenin sahe emeliyyatlarina uygun oldugunu tesdiqlemek lazimdir Belelikle rasional funksiyalarin cemi sifarisli bir sahe teskil edir Qeyd edek ki bu heqiqi ededler sahesinin uzantisidir lakin Arximedin aksiomu burada tetbiq edilmir evvelki hissenin sonuna baxin Heqiqeten 1 displaystyle 1 ve x displaystyle x elementlerini nezerden kecirek Aydindir ki n displaystyle n natural sayi ne olursa olsun berabersizliyi saxlayir 1 1 1 n n 1 lt x displaystyle underbrace 1 1 ldots 1 n n cdot 1 lt x Basqa sozle x displaystyle x birine munasibetde sonsuz boyuk bir sahe elementidir Belelikle bu sahede Arximedin aksiomu tutmur Hemcinin baxArximed Arximed qanunu Arximed spiraliIstinadlarA P Yushkevicha Istoriya matematiki Nauka 2003 seh 96 Evklid Nachala 1 M L Glavnoe Izdatelstvo Tehniko Teoreticheskoj Literatury 1948 Burbaki N Ocherki po istorii matematiki M Izdatelstvo inostrannoj literatury Per I G Bashmakovoj pod red K A Rybnikova 1963 148 Gilbert D Osnovaniya geometrii M L Glavnoe Izdatelstvo Tehniko Teoreticheskoj Literatury 1948 87 EdebiyyatIstoriya matematiki 1 M Nauka Pod red A P Yushkevicha 2003 Evklid Nachala 1 M L Glavnoe Izdatelstvo Tehniko Teoreticheskoj Literatury Perevod D D Morduhaj Boltovskogo 1948 Gilbert D Osnovaniya geometrii M L Glavnoe Izdatelstvo Tehniko Teoreticheskoj Literatury 1948 Burbaki N Ocherki po istorii matematiki M Izdatelstvo inostrannoj literatury Per I G Bashmakovoj pod red K A Rybnikova 1963 Xarici kecidlerArchimede fizika tarixi isp Riyazi Analiz fenninin proqramiPortal Elm Portal FizikaPortal Elm Portal Fizika
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська


