| Parabola, onun fokus məsafəsi və direktrisası | |
 | |
| Kəsik konus: |  |
| Eksentrisitet: | |
| Bərabərlik: | |
| Hiperbola · Parabola · Ellips · Çevrə | |
Parabola (yun. παραβολή, tətbiq) — kvadratik funksiyanın (y = x²) qrafikinə verilən addır. Parabola Hiperbolanın tərsidir. Parabola dedikdə müstəvinin elə nöqtələrinin həndəsi yeri başa düşülür ki, bu nöqtələrin müstəvinin verilmiş düz xəttindən və verilmiş nöqtəsində olan məsafələri bir-birinə bərabər olsun. Müstəvinin verilmiş bu düz xəttinə parabolanın direktirisi, verilmiş nöqtəsinə isə parabolanın fokusu deyilir. Parabolanın fokusunu adətən ilə işarə edirlər.
Bərabərlik
Düzxətli koordinat sistemi üzərində Parabolanın kanonik şəkli aşağıdakı kimidir:
(ya da
, əgər uc nöqtələrinin yernini dəyişdirsək).
| Nəticə |
|---|
 Direktrisanın bərabərliyi:
|
Kvadrat tənlik: 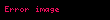


haradakı:
— Diskriminant. Həmçinin:
kvadratik tənliyi
bu şəkildə də göstərilə bilər. Əgər
nöqtəsi koordinat siteminin başlanğıcı üzərində olarsa kanonik şəkildə göstərilə bilər. Bu zaman:
ifadəsi meydana çıxır.
Kvadrat tənliyinin əmsallarının hesablanması
Əgər 



Digər bərabərliklər
Şaquli simmetriyanın ucları
haradakı:
. Parametrik forması:
Üfüqi simmetriyanın ucları
haradakı:
. Parametrik forması:
Baş parabola
Parabola üçün ümumi düstur aşağıdakı kimidir:
və aşağıdakı kimi ifadə üçün doğrudur,
.
Baş parabola üçün fokus tənliyi: F(u, v), və a direktriks üçün düstur:
is
Qauss xəritəsinin forması
Qauss xəritəsinin forması aşağıdakı kimidir: 

Polyar koordinatda parabola
Polyar koordinatda olan parabola üçün aşağıdakı bərabərliklər vardır:
Fəzada Parabola
Bir sıra kosmik cisimlərin trayektoriyası (kometlər, asteroidlər və s.) böyük sürətlə parabolaya oxşayırlar. Parabola konus ailəsinin bir hissəsinə aiddir. Parabolanın formasından bir sıra arxitekturada istifadə edilir.
-
![image]() Parabolik orbit
Parabolik orbit -
![image]() Basketbol topunun düşməsi
Basketbol topunun düşməsi -
![image]()
-
![image]()
-
![image]()
- Parabolanın konus şəkli
Həmçinin bax
Xarici keçidlər

- Animierte Parabel
- *
- Interactive parabola-drag focus, see axis of symmetry, directrix, standard and vertex forms
- Archimedes Triangle and Squaring of Parabola
- Two Tangents to Parabola
- Parabola As Envelope of Straight Lines
- Parabolic Mirror
- Three Parabola Tangents
- Module for the Tangent Parabola
- Focal Properties of Parabola
- Parabola As Envelope II
- The similarity of parabola
- Dynamic Geometry Sketches, interactive dynamic geometry sketch.
- a method of drawing a parabola with string and tacks 2010-09-01 at the Wayback Machine
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Parabola onun fokus mesafesi ve direktrisasiKesik konus Eksentrisitet e 1 displaystyle textstyle e 1 Beraberlik y2 2px displaystyle textstyle y 2 2px Hiperbola Parabola Ellips Cevre Parabola yun parabolh tetbiq kvadratik funksiyanin y x qrafikine verilen addir Parabola Hiperbolanin tersidir Parabola dedikde mustevinin ele noqtelerinin hendesi yeri basa dusulur ki bu noqtelerin mustevinin verilmis duz xettinden ve verilmis noqtesinde olan mesafeleri bir birine beraber olsun Mustevinin verilmis bu duz xettine parabolanin direktirisi verilmis noqtesine ise parabolanin fokusu deyilir Parabolanin fokusunu adeten F displaystyle F ile isare edirler BeraberlikDuzxetli koordinat sistemi uzerinde Parabolanin kanonik sekli asagidaki kimidir y2 2px p gt 0 displaystyle textstyle y 2 2px p gt 0 ya da x2 2py displaystyle textstyle x 2 2py eger uc noqtelerinin yernini deyisdirsek NeticeDirektrisanin beraberliyi PQ displaystyle PQ x p2 0 displaystyle textstyle x frac p 2 0 fokus F p2 0 displaystyle textstyle F left frac p 2 0 right buna esasen koordinat baslangici O displaystyle O merkezin kesiyi CF displaystyle CF Parabolanin M displaystyle M ucun tapilmis muxtelif noqtesinde uzerinde yerlesen beraberlik alinir KM FM displaystyle KM FM KM KD DM p2 x displaystyle textstyle KM KD DM frac p 2 x ve FM x p2 2 y2 displaystyle textstyle FM sqrt left x frac p 2 right 2 y 2 onda beraberlik asgidaki gorunusunu alir x p2 2 y2 p2 x displaystyle sqrt left x frac p 2 right 2 y 2 frac p 2 x Beraberliyi muxtelif cur hesabladiqdan sonra eyniguclu beraberlik alinir y2 2px displaystyle y 2 2px Kvadrat tenlik y ax2 bx c displaystyle y ax 2 bx c pri a 0 displaystyle a neq 0 hemcinin parabolanin i qrafikini eks etdirir bu dustur kimi y ax2 displaystyle y ax 2 ancaq birinci beraberlik ikinci beraberlikden ona gore ferqlenir ki birinci beraberliyin baslangici koordinat baslangici uzerinde deyildir A displaystyle A nin muxtelif noqteleri ucun koordinat asagidaki dusturla hesablanir xA b2a yA D4a displaystyle x A frac b 2a y A frac D 4a haradaki D b2 4ac displaystyle D b 2 4ac Diskriminant Hemcinin y ax2 bx c displaystyle y ax 2 bx c kvadratik tenliyi y a x xA 2 yA displaystyle y a x x A 2 y A bu sekilde de gosterile biler Eger A displaystyle A noqtesi koordinat siteminin baslangici uzerinde olarsa kanonik sekilde gosterile biler Bu zaman p 1 2a displaystyle p frac 1 2a ifadesi meydana cixir Kvadrat tenliyinin emsallarinin hesablanmasi Eger y ax2 bx c displaystyle y ax 2 bx c tenliyi ucun tapilmis uc noqte ucun x1 y1 displaystyle x 1 y 1 x2 y2 displaystyle x 2 y 2 x3 y3 displaystyle x 3 y 3 ifadeler alinarsa onda kvadrat tenliyinin emsallarini asagidaki kimi hesablamaq olar a y3 x3 y2 y1 x2y1 x1y2x2 x1x3 x3 x1 x2 x1x2 b y2 y1x2 x1 a x1 x2 c x2y1 x1y2x2 x1 ax1x2 displaystyle a frac y 3 frac x 3 y 2 y 1 x 2 y 1 x 1 y 2 x 2 x 1 x 3 x 3 x 1 x 2 x 1 x 2 b frac y 2 y 1 x 2 x 1 a x 1 x 2 c frac x 2 y 1 x 1 y 2 x 2 x 1 ax 1 x 2 Diger beraberliklerSaquli simmetriyanin uclari x h 2 4p y k displaystyle x h 2 4p y k y x h 24p k displaystyle y frac x h 2 4p k y ax2 bx c displaystyle y ax 2 bx c haradaki a 14p b h2p c h24p k displaystyle a frac 1 4p b frac h 2p c frac h 2 4p k h b2a k 4ac b24a displaystyle h frac b 2a k frac 4ac b 2 4a Parametrik formasi x t 2pt h y t pt2 k displaystyle x t 2pt h y t pt 2 k Ufuqi simmetriyanin uclari y k 2 4p x h displaystyle y k 2 4p x h x y k 24p h displaystyle x frac y k 2 4p h x ay2 by c displaystyle x ay 2 by c haradaki a 14p b k2p c k24p h displaystyle a frac 1 4p b frac k 2p c frac k 2 4p h h 4ac b24a k b2a displaystyle h frac 4ac b 2 4a k frac b 2a Parametrik formasi x t pt2 h y t 2pt k displaystyle x t pt 2 h y t 2pt k Bas parabola Parabola ucun umumi dustur asagidaki kimidir ax by 2 gx dy ϵ 0 displaystyle alpha x beta y 2 gamma x delta y epsilon 0 Ax2 Bxy Cy2 Dx Ey F 0 displaystyle Ax 2 Bxy Cy 2 Dx Ey F 0 ve asagidaki kimi ifade ucun dogrudur B2 4AC displaystyle B 2 4AC Bas parabola ucun fokus tenliyi F u v ve a direktriks ucun dustur ax by c 0 displaystyle ax by c 0 is ax by c 2a2 b2 x u 2 y v 2 displaystyle frac left ax by c right 2 a 2 b 2 left x u right 2 left y v right 2 Qauss xeritesinin formasi Qauss xeritesinin formasi asagidaki kimidir tan2 ϕ 2tan ϕ displaystyle tan 2 phi 2 tan phi tenliyin ifadesi asagidaki ifade kimi eynigucludur cos ϕ sin ϕ displaystyle cos phi sin phi Polyar koordinatda parabolaPolyar koordinatda olan parabola ucun asagidaki beraberlikler vardir r f 4acos f sin2 f f p2 p2 0 displaystyle r varphi 4a frac cos varphi sin 2 varphi quad varphi in left tfrac pi 2 tfrac pi 2 right setminus 0 a 0 displaystyle a 0 r f 2a1 cos f f 2pk displaystyle r varphi frac 2a 1 cos varphi quad varphi neq 2 pi k Fezada ParabolaBir sira kosmik cisimlerin trayektoriyasi kometler asteroidler ve s boyuk suretle parabolaya oxsayirlar Parabola konus ailesinin bir hissesine aiddir Parabolanin formasindan bir sira arxitekturada istifade edilir Parabolik orbit Basketbol topunun dusmesi Parabolanin konus sekliHemcinin baxHiperbolaXarici kecidlerVikianbarda Parabola ile elaqeli mediafayllar var Animierte Parabel Interactive parabola drag focus see axis of symmetry directrix standard and vertex forms Archimedes Triangle and Squaring of Parabola Two Tangents to Parabola Parabola As Envelope of Straight Lines Parabolic Mirror Three Parabola Tangents Module for the Tangent Parabola Focal Properties of Parabola Parabola As Envelope II The similarity of parabola Dynamic Geometry Sketches interactive dynamic geometry sketch a method of drawing a parabola with string and tacks 2010 09 01 at the Wayback Machine
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State