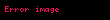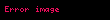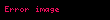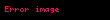Ekonometrika (ekonometriya) — iqtisadi proseslərin və göstəricilərin statistik və riyazi üsullarla, son zamanlar isə kompüter elmləri ilə təhlilini və şərh olunmasını təmin edən elm sahəsidir. İndiki dövrdə daha güclü kompüter və proqram təminatlarının varlığıyla gücünü artmışdır. Ekonometriya iki – "ekonomiya" (iqtisadiyyat) və "metrika" (ölçmə) sözlərindən yaranıb. Məşhur Norveç alimi, Nobel mükafatı laureatı Raqnar Friş tərəfindən elmə daxil edilmişdir. Ekonometriya elmi XX əsrin əvvəllərində xətti proqramlaşdırma məsələsinin, yaranması və onların real iqtisadi proseslərə tətbiqi ilə yaranmışdır. Ekonometriya termininin əvəzinə bəzən "ekonometrika" termini də işlədilir.
| İqtisadiyyat | |
|---|---|
 | |
| Əsas kateqoriyalar | |
| Mikroiqtisadiyyat | |
| Makroiqtisadiyyat | |
| İqtisadi təlimlər tarixi | |
| İqtisadi metodologiya | |
| Alternativ iqtisadiyyat | |
| Texniki metodlar | |
| Riyazi iqtisadiyyat | |
| Ekonometrika | |
| Təcrübi iqtisadiyyat | |
| Milli Hesablar Sistemi | |
| Sahələr və alt sahələr | |
| Təhsil | |
| Səhiyyə | |
| Əmək | |
| Oyunlar nəzəriyyəsi | |
| Artım | |
| Kənd təsərrüfatı | |
| Təbii ehtiyatlar | |
| Davranış | |
| İqtisadi sistem | |
| Beynəlxalq | |
Onun predmeti iqtisadi təzahürlərin və proseslərin kəmiyyət tərəfini riyazi və statistik üsullarla öyrənməkdən ibarətdir. Bu, iqtisadiyyat elminin yeni istiqamətidir. Ekonometrika riyazi iqtisadiyyatdan real, iqtisadi proseslərə ehtimal nəzəriyyəsi və statistik üsulların tətbiqi ilə fərqlənir.
olaraq "iqtisadi ölçüm" mənasını verir. Riyazi iqtisad, statistika və iqtisadi nəzəriyyənin birləşməsindən meydana gələr. İqtisadi nəzəriyyənin empirik analizlə sınanmasını mümkün edir.
Ekonometrik modellər
Ekonometrinin ən çox istifadə edilən üsul .
Ekonometrik təhlillər iki ana budaqda araşdırıla bilər. Birincisi zaman sıraları təhlilləri, digəri isə təhlilləridir. Zaman sıraları təhlilləri dəyişənlərin bir zaman aralığı üzərindəki dəyərlərini və bu dəyərlərin fərqli dəyişənlər üçün bir-birləriylə müqayisə edilməsinə əsaslanır. Köndələn kəsik təhlilləri isə vahid bir zaman nöqtəsində fərqli dəyişənlərin araşdırılmasına əsaslanır. Məsələn 1990–2000 illəri arasında iqtisadi böyümə və məşğulluq arasındakı əlaqə tək bir ölkə üçün araşdırıldığında zaman sıraları analizi, 1990-cu ili üzərində fərqli ölkələrin məşğulluq və iqtisadi böyümə rəqəmləri araşdırıldığında köndələn kəsik analizi edilmiş olar.
Zaman sıraları və köndələn kəsik məlumatları bir yerdə istifadə edildiyində isə panel data analizi deyilən üsul tətbiq olunar. Nümunəyə görə bu analiz 1990-cu ilə 2000-ci illəri arasında 20 fərqli ölkənin məşğulluq və iqtisadi böyümə rəqəmləri analiz edildiyində panel məlumat üsullarından istifadə edilir.
Xətti reqressiya modelləri
Ekonometrikada bir çox statistik alətlər istifadə edilsədə, ən çox istifadə edilən .
Nümunə üçün İqtisadi artım ilə isizlik səviyyəsində arasında əlaqəni göstərən nəzər salaq. Bu münasibət xətti reqressiya formasında göstərir ki, işsizlik səviyyəsindəki dəyişmə (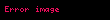
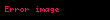
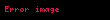

Burada 

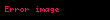
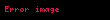
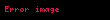
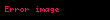
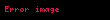
Nəzəriyyə
Ekonometrik nəzəriyyə statistik nəzəriyyədən istifadə edərək ekonometrik üsullar yaradaraq onları qiymətləndirir. Ekonometriklər meyilli olmayan, tutarlı və səmərəli kimi xüsusiyyətləri olan qiymətləndirəni tapmağa çalışırlar. , və . Qiymətləndirənin riyazi gözləməsi əgər həqiqi parametrə bərabər olarsa, o zaman bu qiymətləndirən meylsiz qiymətləndirən olur. Qiymətləndirən o zaman tutatlı sayılır ki, seçmədə müşahidə sayı artdıqca həqiqi paramatrə yığılır, və qiymətləndirən o zaman səmərəli sayılır ki, onun standart xətası verilmiş seçmə müşahidədə digər meyilsiz qiyməltəndirənlərin standart xətalarından daha aşağıdır. Qiymətləndirmə üçün ən çox (ƏKKÜ) istifadə edilir, çünki Qaus-Markov fərziyyələri verildiyi təqdirdə ƏKKÜ "ən yaxşı xətti meylsiz qiymətləndirəni" təmin edir (burada "ən yaxşı" ən səmərəli olanı, meylsiz qiymətləndirəni bildirir). Bu fərziyyələr pozulduqda vəya ödənmədikdə digər üsullara, , , və ya üsulları istifadə edilir. əsaslanaraq digər ənənəvi, klassik və ya məktəbinə üstünlük verirlər.
Qaus–Markov teoremi
göstərir ki, modelin olmasını fərz edərək ƏKKÜ qiymətləndirməsi ən yaxşı (minimum varyans), meylsiz qiymətləndirmədir, xətaların riyazi gözləməsi sıfırdır, xətalar , və yoxdur, və mükəmməl problemi yoxdur.
Xəttilik
Asılı dəyişən asılı olmayan dəyişənlərin xətti funksiyası kimi fərz edilir. Xəttilik deyilərkən, əmsallarda xəttilik nəzərdə tutulut. Əmsallar (parametr) xətti olduqları müddətcə asılı olmayan dəyişənlər arasında əlaqə hətta qeyri xətti də ola bilər. 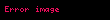
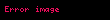
adətən tənliyi xətti şəkilə gətirilməsində istifadə edilir (bax , Santos Silva and Tenreyro, 2006). Məsələn, qeyri xəttidir:
Ancaq funkisyanın hər iki tərəfini götürməklə xətti hala transformasiya etmək mümkündür: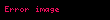
Bu fərziyyə həmçinin müəyyən spesifikasiya problemlərini də həll edir: fərz edərək ki, uyğun seçilmişdir və problemi yoxdur.
Xətaların riyazi gözləməsi sıfırdır
Xətaların riyazi gözləməsi sıfır olduğu fərz edilir. Yanlış ölçmə nəticəsi səbəbi ilə sabit əmsal meylli ola bilər, ancaq digər əmsallar meyilsiz olaraq qalacaqlardır.
Sabit əmsal həmçinin laqorifmik transformasiya səbəbi ilə də meylli ola bilər. Yuxarıda Kobb-Duqlas tənliyinə diqqət edin. Multiplikativ səhv sıfır ortaya sahib olmayacaq, buna görədə bu fərziyyə özünü doğrultmayacaq.
Sferik xətalar
Xətalar sferik olduğu fərz edilir, əks halda ƏKKÜ səmərəsiz nəticə verəcəkdir. Ancaq, ƏKKÜ meyilsiz olaraq qalacaqdır. Sferik xətalar o zaman yaranır ki, həm xətalar yekcins varyansa () sahibdir , həm də bir birləri ilə korrelasiya etmir. "Sferik xətalar" o halda çoxdəyişənli normal paylanmanı təsvri edir ki: əgər 
Heteroskedastiklik o zaman yaranır ki, xətalar asılı olmayan dəyişən ilə korrelyasiya edir. Heteroskedastiklik məlumatlarda ölçmə səbəbləri ilə də böyüyə bilər. Ancaq sttistika mərkəzləri məlumatlarını keyfiyyətini artırdıqca ölçü xətaları azalacaq və beləcə reqressiya xətasıda azalacaqdır.
Sferik xətalar fərziyəsi həmçinin xətalar arasında olduğu təqdirdə pozulur. Zaman sıralarında "inersiya" olduğu təqdirdə avtokorrelyasiya bu sıralar üçün ümumi bir xüsusiyyət olur. Avtokorrelyasiya funksiyonal formanın düzgün spesifikasiya edilməməsindən dolayı ola bilər. Bu halda düzgün spesifikasiya formasının seçilməsi avtokorrelyasiya probleminin həll edilməsi üçün mümkün yollardan biridir.
Qeyri-sferik xətaların mövcudluğu zamanı, ümumiləşdirilmiş ən kiçik kvadratlar üsulu Ən yaxşı Xətti Meylsiz Qiymətləndirən (ƏXMQ) kimi ola bilər.
Asılı olmayan dəyişənlərin eqzogenliyi
Bu fərziyyə dəyişənlər . olduğu təqdirdə pozulur. Endogenlik asılı və asılı olmayan dəyişənlərin keçmiş və gələcək dəyərləri arasında səbəbiyyət əlaqəsinin, yəni nəticəsi olaraq yaranır. bu problemi aşmaq üçün ən çox istifadə edilən üsullardandır.
Tam ranq
Seçmə müşahidə məlumat matrisi tam olmalıdır əks halda ƏKKÜ hesablaan bilməz. Matrisdə hər bir parameter üçün ən azı bir müşahidə mövcud olmalıdır və məlumatlar arasında mükəmməl multikollinarlıq olmamalıdır. Multikolliniarlıq ("mükəmməl" olmadığı müddətcə) səmərəli, lakin hələ də meylsiz qiymətləndirmələr verə bilər.
İstinadlar
- "/ Ekonometrik modellər. Korrelyasiya və reqresiya təhlilinin əsas məsələsi". 2022-03-31 tarixində . İstifadə tarixi: 2012-01-08.
- Greene (2012), 12.
- Kennedy, 2003. səh. 110
- Kennedy, 2003. səh. 129
- Kennedy, 2003. səh. 131
- Kennedy, 2003. səh. 133
- Greene, 2012. səh. 23-note
- Greene, 2010. səh. 22
- Kennedy, 2003. səh. 135
- Kennedy, 2003. səh. 205
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Ekonometrika ekonometriya iqtisadi proseslerin ve gostericilerin statistik ve riyazi usullarla son zamanlar ise komputer elmleri ile tehlilini ve serh olunmasini temin eden elm sahesidir Indiki dovrde daha guclu komputer ve proqram teminatlarinin varligiyla gucunu artmisdir Ekonometriya iki ekonomiya iqtisadiyyat ve metrika olcme sozlerinden yaranib Meshur Norvec alimi Nobel mukafati laureati Raqnar Fris terefinden elme daxil edilmisdir Ekonometriya elmi XX esrin evvellerinde xetti proqramlasdirma meselesinin yaranmasi ve onlarin real iqtisadi proseslere tetbiqi ile yaranmisdir Ekonometriya termininin evezine bezen ekonometrika termini de isledilir IqtisadiyyatEsas kateqoriyalarMikroiqtisadiyyatMakroiqtisadiyyatIqtisadi telimler tarixiIqtisadi metodologiyaAlternativ iqtisadiyyatTexniki metodlarRiyazi iqtisadiyyatEkonometrikaTecrubi iqtisadiyyatMilli Hesablar SistemiSaheler ve alt sahelerTehsilSehiyyeEmekOyunlar nezeriyyesiArtimKend teserrufatiTebii ehtiyatlarDavranisIqtisadi sistemBeynelxalqbr Onun predmeti iqtisadi tezahurlerin ve proseslerin kemiyyet terefini riyazi ve statistik usullarla oyrenmekden ibaretdir Bu iqtisadiyyat elminin yeni istiqametidir Ekonometrika riyazi iqtisadiyyatdan real iqtisadi proseslere ehtimal nezeriyyesi ve statistik usullarin tetbiqi ile ferqlenir olaraq iqtisadi olcum menasini verir Riyazi iqtisad statistika ve iqtisadi nezeriyyenin birlesmesinden meydana geler Iqtisadi nezeriyyenin empirik analizle sinanmasini mumkun edir Ekonometrik modellerEsas meqale Ekonometrinin en cox istifade edilen usul Ekonometrik tehliller iki ana budaqda arasdirila biler Birincisi zaman siralari tehlilleri digeri ise tehlilleridir Zaman siralari tehlilleri deyisenlerin bir zaman araligi uzerindeki deyerlerini ve bu deyerlerin ferqli deyisenler ucun bir birleriyle muqayise edilmesine esaslanir Kondelen kesik tehlilleri ise vahid bir zaman noqtesinde ferqli deyisenlerin arasdirilmasina esaslanir Meselen 1990 2000 illeri arasinda iqtisadi boyume ve mesgulluq arasindaki elaqe tek bir olke ucun arasdirildiginda zaman siralari analizi 1990 cu ili uzerinde ferqli olkelerin mesgulluq ve iqtisadi boyume reqemleri arasdirildiginda kondelen kesik analizi edilmis olar Zaman siralari ve kondelen kesik melumatlari bir yerde istifade edildiyinde ise panel data analizi deyilen usul tetbiq olunar Numuneye gore bu analiz 1990 cu ile 2000 ci illeri arasinda 20 ferqli olkenin mesgulluq ve iqtisadi boyume reqemleri analiz edildiyinde panel melumat usullarindan istifade edilir Xetti reqressiya modelleri Ekonometrikada bir cox statistik aletler istifade edilsede en cox istifade edilen Numune ucun Iqtisadi artim ile isizlik seviyyesinde arasinda elaqeni gosteren nezer salaq Bu munasibet xetti reqressiya formasinda gosterir ki issizlik seviyyesindeki deyisme D U displaystyle Delta U sabit emsalin b0 displaystyle beta 0 UDM artiminin verilmis deyeri vurulsun emsal b1 displaystyle beta 1 ve tesadufi xeta deyerlerinin ϵ displaystyle epsilon funksiyasidir D U b0 b1G e displaystyle Delta U beta 0 beta 1 text G varepsilon Burada U displaystyle U issizlik seviyyesini G displaystyle G ise UDM artimini bildirir Bilinmeyen parametrler b0 displaystyle beta 0 ve b1 displaystyle beta 1 qiymetlendirile biler Burada b1 displaystyle beta 1 emsali 1 77 ve b0 displaystyle beta 0 ise 0 83 qiymetlendirme neticesinde tapildigini ferz edek Bu o demekdir ki UDM Artimi bir faiz deyeri qeder artacagi teqdirde issizlik seviyyesi 94 qeder azalacagi proqnozlasdirila biler 1 77 1 0 83 Daha sonra model vasitesile esas hipotezi iqtisadi artimda artimin issizlikde azalmaya sebeb olmasinin yoxlamaq mumkundur Eger qiymetlendirilen b1 displaystyle beta 1 0 dan ehemiyyeli derecede ferqli deyilse test iqtisadi artimda deyismenin issizlikdeki deyisme ile elaqeli oldugunu subut tapmaqda ugursuz olacaqdir NezeriyyeEkonometrik nezeriyye statistik nezeriyyeden istifade ederek ekonometrik usullar yaradaraq onlari qiymetlendirir Ekonometrikler meyilli olmayan tutarli ve semereli kimi xususiyyetleri olan qiymetlendireni tapmaga calisirlar ve Qiymetlendirenin riyazi gozlemesi eger heqiqi parametre beraber olarsa o zaman bu qiymetlendiren meylsiz qiymetlendiren olur Qiymetlendiren o zaman tutatli sayilir ki secmede musahide sayi artdiqca heqiqi paramatre yigilir ve qiymetlendiren o zaman semereli sayilir ki onun standart xetasi verilmis secme musahidede diger meyilsiz qiymeltendirenlerin standart xetalarindan daha asagidir Qiymetlendirme ucun en cox EKKU istifade edilir cunki Qaus Markov ferziyyeleri verildiyi teqdirde EKKU en yaxsi xetti meylsiz qiymetlendireni temin edir burada en yaxsi en semereli olani meylsiz qiymetlendireni bildirir Bu ferziyyeler pozulduqda veya odenmedikde diger usullara ve ya usullari istifade edilir esaslanaraq diger enenevi klassik ve ya mektebine ustunluk verirler Qaus Markov teoremi gosterir ki modelin olmasini ferz ederek EKKU qiymetlendirmesi en yaxsi minimum varyans meylsiz qiymetlendirmedir xetalarin riyazi gozlemesi sifirdir xetalar ve yoxdur ve mukemmel problemi yoxdur Xettilik Asili deyisen asili olmayan deyisenlerin xetti funksiyasi kimi ferz edilir Xettilik deyilerken emsallarda xettilik nezerde tutulut Emsallar parametr xetti olduqlari muddetce asili olmayan deyisenler arasinda elaqe hetta qeyri xetti de ola biler y a bx2 displaystyle y alpha beta x 2 tenliyi xetti oldugu halda y a b2x displaystyle y alpha beta 2 x tenliyinin beta emsalinin diger bir emsalla meselen qamma ile evezledikde xetti formaya cevirmek mumkundur Tenliyin emsali asili olmayan deyisenden asili oldugu teqdirde tenlik artiq xetti hesab edilmir meselen y alpha beta x x burada beta x emsali x deyisenin funksiyasidir adeten tenliyi xetti sekile getirilmesinde istifade edilir bax Santos Silva and Tenreyro 2006 Meselen qeyri xettidir Y ALaKbe displaystyle Y AL alpha K beta varepsilon Ancaq funkisyanin her iki terefini goturmekle xetti hala transformasiya etmek mumkundur lnY lnA alnL blnK lne displaystyle lnY lnA alpha lnL beta lnK ln varepsilon Bu ferziyye hemcinin mueyyen spesifikasiya problemlerini de hell edir ferz ederek ki uygun secilmisdir ve problemi yoxdur Xetalarin riyazi gozlemesi sifirdir E e 0 displaystyle operatorname E varepsilon 0 Xetalarin riyazi gozlemesi sifir oldugu ferz edilir Yanlis olcme neticesi sebebi ile sabit emsal meylli ola biler ancaq diger emsallar meyilsiz olaraq qalacaqlardir Sabit emsal hemcinin laqorifmik transformasiya sebebi ile de meylli ola biler Yuxarida Kobb Duqlas tenliyine diqqet edin Multiplikativ sehv sifir ortaya sahib olmayacaq buna gorede bu ferziyye ozunu dogrultmayacaq Sferik xetalar Var e X s2In displaystyle operatorname Var varepsilon X sigma 2 I n Xetalar sferik oldugu ferz edilir eks halda EKKU semeresiz netice verecekdir Ancaq EKKU meyilsiz olaraq qalacaqdir Sferik xetalar o zaman yaranir ki hem xetalar yekcins varyansa sahibdir hem de bir birleri ile korrelasiya etmir Sferik xetalar o halda coxdeyisenli normal paylanmani tesvri edir ki eger Var e X s2In displaystyle operatorname Var varepsilon X sigma 2 I n coxdeyisenli normal sixliqda o zaman f x c tenliyi n olculu fezada ortasi m radiusu s olan kuredir Heteroskedastiklik o zaman yaranir ki xetalar asili olmayan deyisen ile korrelyasiya edir Heteroskedastiklik melumatlarda olcme sebebleri ile de boyuye biler Ancaq sttistika merkezleri melumatlarini keyfiyyetini artirdiqca olcu xetalari azalacaq ve belece reqressiya xetasida azalacaqdir Sferik xetalar ferziyesi hemcinin xetalar arasinda oldugu teqdirde pozulur Zaman siralarinda inersiya oldugu teqdirde avtokorrelyasiya bu siralar ucun umumi bir xususiyyet olur Avtokorrelyasiya funksiyonal formanin duzgun spesifikasiya edilmemesinden dolayi ola biler Bu halda duzgun spesifikasiya formasinin secilmesi avtokorrelyasiya probleminin hell edilmesi ucun mumkun yollardan biridir Qeyri sferik xetalarin movcudlugu zamani umumilesdirilmis en kicik kvadratlar usulu En yaxsi Xetti Meylsiz Qiymetlendiren EXMQ kimi ola biler Asili olmayan deyisenlerin eqzogenliyi E e X 0 displaystyle operatorname E varepsilon X 0 Bu ferziyye deyisenler oldugu teqdirde pozulur Endogenlik asili ve asili olmayan deyisenlerin kecmis ve gelecek deyerleri arasinda sebebiyyet elaqesinin yeni neticesi olaraq yaranir bu problemi asmaq ucun en cox istifade edilen usullardandir Tam ranq Secme musahide melumat matrisi tam olmalidir eks halda EKKU hesablaan bilmez Matrisde her bir parameter ucun en azi bir musahide movcud olmalidir ve melumatlar arasinda mukemmel multikollinarliq olmamalidir Multikolliniarliq mukemmel olmadigi muddetce semereli lakin hele de meylsiz qiymetlendirmeler vere biler Istinadlar Ekonometrik modeller Korrelyasiya ve reqresiya tehlilinin esas meselesi 2022 03 31 tarixinde Istifade tarixi 2012 01 08 Greene 2012 12 Kennedy 2003 seh 110 Kennedy 2003 seh 129 Kennedy 2003 seh 131 Kennedy 2003 seh 133 Greene 2012 seh 23 note Greene 2010 seh 22 Kennedy 2003 seh 135 Kennedy 2003 seh 205
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State