Zaman sıraları — müəyyən göstərici sırası olub, ardıcıl nöqtələrin bircinsli zaman intervallarında təyin edilməsi ilə ölçülür. Bu zaman intervalları günlük, aylıq və illik kimi təyin edilə bilər. Zaman sıraları statistika, ekonometrika, riyazi maliyyə, hava proqnozu, , astronomiya, iqtisadiyyat, mühəndislik və sair müxtəlif elm sahələrində geniş istifadə olunur.
Zaman sıraları təhlilləri göstəricilərin əhəmiyyətli statistik və digər xüsusiyyətlərini üzə çıxarmaq məqsədi ilə zaman sıralarının təhlilinə imkan verən müxtəlif üsulları ehtiva edir. Zaman sıralarının proqnozlaşdırılması göstəricinin keçmiş müşahidə edilən qiymətlərinə əsaslanaraq gələcək qiymətlərinin təxmin edilməsi üçün nəzərdə tutulan . isə adətən bir vəya bir neçə asılı olmayan zaman sıralarının indiki dəyərinin digər zaman sıralarının indiki dəyərinə təsirini müəyyən etmək üçün istifadə edilir, bu kimi təhlillər "zaman sıraları təhlilləri" adlanmır, çünki "zaman sıraları təhlilləri" zaman sıralarının müxtəlif zamanlarda dəyərlərini müqayisə edir.
İşarələmə
Zaman sıraları təhlillərində müxtəlif işarəmələrdən istifadə olunur. göstəricisinin zaman sırası ümumi olaraq indekslənmiş şəkildə ifadə olunur
- .
Ancaq yuxarıdakı işarələmə tez-tez çoxdəyişənli mənasını da verdiyi üçün daha çox aşağıdakı formaya üstünlük verilir
- ,
burada .
Nümunə
Modellər
AR(p) ümumi yazılış forması aşağıdakı kimidir
burada ifadəsi təsadüfliyin bir növü olub ağ küy adlanır. Fərz edilir ki, ağ küy aşağıdakı xassələrə malikdir:
Bu fərziyyələr ilə, proses ikinci tərtib momentə kimi ifadə edilir və əmsallar üzərində şərtlərdən asılı olur, və ola bilsin ki, proses zəif stasionardır ().
Əgər küy həmçinin normal paylanmaya sahibdirsə, buna normal və ya Qaus ağ küyü adlanır. Bu halda AR prosesi şərtinə cavab verir, və əmsallar üzərində şərtlərdən asılı olur.
Mənbə
- Imdadullah. "Time Series Analysis". Basic Statistics and Data Analysis. 2014-01-02 tarixində . İstifadə tarixi: 2014-02-19.
Xarici Keçidlər
- Tətbiqi Ekonometrika
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Zaman siralari mueyyen gosterici sirasi olub ardicil noqtelerin bircinsli zaman intervallarinda teyin edilmesi ile olculur Bu zaman intervallari gunluk ayliq ve illik kimi teyin edile biler Zaman siralari statistika ekonometrika riyazi maliyye hava proqnozu astronomiya iqtisadiyyat muhendislik ve sair muxtelif elm sahelerinde genis istifade olunur Zaman siralari tehlilleri gostericilerin ehemiyyetli statistik ve diger xususiyyetlerini uze cixarmaq meqsedi ile zaman siralarinin tehliline imkan veren muxtelif usullari ehtiva edir Zaman siralarinin proqnozlasdirilmasi gostericinin kecmis musahide edilen qiymetlerine esaslanaraq gelecek qiymetlerinin texmin edilmesi ucun nezerde tutulan ise adeten bir veya bir nece asili olmayan zaman siralarinin indiki deyerinin diger zaman siralarinin indiki deyerine tesirini mueyyen etmek ucun istifade edilir bu kimi tehliller zaman siralari tehlilleri adlanmir cunki zaman siralari tehlilleri zaman siralarinin muxtelif zamanlarda deyerlerini muqayise edir Isareleme Zaman siralari tehlillerinde muxtelif isaremelerden istifade olunur X displaystyle X gostericisinin zaman sirasi umumi olaraq indekslenmis sekilde ifade olunur X X1 X2 displaystyle X X 1 X 2 Ancaq yuxaridaki isareleme tez tez coxdeyisenli menasini da verdiyi ucun daha cox asagidaki formaya ustunluk verilir Y Yt t T displaystyle Y Y t t in T burada T displaystyle T Numune Y Y2000 Y2001 Y2002 displaystyle Y Y 2000 Y 2001 Y 2002 Modeller AR p umumi yazilis formasi asagidaki kimidir Yt a0 a1Yt 1 a2Yt 2 apYt p et displaystyle Y t alpha 0 alpha 1 Y t 1 alpha 2 Y t 2 cdots alpha p Y t p varepsilon t burada et displaystyle varepsilon t ifadesi tesadufliyin bir novu olub ag kuy adlanir Ferz edilir ki ag kuy asagidaki xasselere malikdir E et 0 displaystyle E varepsilon t 0 E et2 s2 displaystyle E varepsilon t 2 sigma 2 E etes 0 for all t s displaystyle E varepsilon t varepsilon s 0 quad text for all t not s Bu ferziyyeler ile proses ikinci tertib momente kimi ifade edilir ve emsallar uzerinde sertlerden asili olur ve ola bilsin ki proses zeif stasionardir Eger kuy hemcinin normal paylanmaya sahibdirse buna normal ve ya Qaus ag kuyu adlanir Bu halda AR prosesi sertine cavab verir ve emsallar uzerinde sertlerden asili olur MenbeImdadullah Time Series Analysis Basic Statistics and Data Analysis 2014 01 02 tarixinde Istifade tarixi 2014 02 19 Xarici KecidlerTetbiqi Ekonometrika
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State
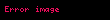
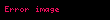
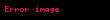
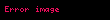
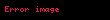
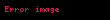
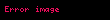
![{\displaystyle E[\varepsilon _{t}]=0\,,}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4eVptWXhNRFptWW1RNE56a3pNVFpoT0RGa1l6azRZV1l3TW1WaE5qUTJNRE5rWVdVM05qRmguc3Zn.svg)
![{\displaystyle E[\varepsilon _{t}^{2}]=\sigma ^{2}\,,}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5aE5UY3pNbUV4WW1GbE1qTXhOMlJsTWpWbFlqaGlNekZtTkRSaFltVTVOVE13Tldaak5UWTQuc3Zn.svg)
![{\displaystyle E[\varepsilon _{t}\varepsilon _{s}]=0\quad {\text{ for all }}t\not =s\,.}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4ME1qRXpNV0ZoWmpSak5qQXhOemN5T1RjeVl6WTFZVE0yTWpNeFpXWmpZak13WVRNMU1tTXouc3Zn.svg)