Üçbucaq — Müstəvinin bir düz xətt üzərində olmayan 3 nöqtəsini cüt-cüt və ardıcıl şəkildə birləşdirən 3 düz xətt parçasından ibarət fiqur. Nöqtələr onun təpələri, parçalar onun tərəfləridir.
Üçbucağın təpələri adətən böyük latın hərfləri ilə (A, B, C), uyğun təpədəki bucaqların dərəcə ölçüsü yunan hərfləri (α,β,γ) ilə, uyğun təpənin qarşısındakı tərəfin uzunluğu isə əlyazma latın hərfləri ilə (a, b, c) işarə olunur.
Üçbucağın növləri
| Üçbucağın növləri | ||
|---|---|---|
 İtibucaqlı üçbucaq |  Korbucaqlı üçbucaq |  Düzbucaqlı üçbucaq |
 Müxtəliftərəfli üçbucaq | Bərabəryanlı üçbucaq |  Bərabərtərəfli üçbucaq |
- Bütün bucaqları iti bucaq (90-dərəcədən kiçik) olan üçbucağa itibucaqlı üçbucaq deyilir.
- Bir bucağı düz bucaq (90°-yə bərabər) olan üçbucağa düzbucaqlı üçbucaq deyilir. Üçbucağın yalnız bir bucağı düz bucaq ola bilər. Düzbucaqlı üçbucağın qalan iki bucağı iti (90°-dən az) bucaqdır.
- Bir bucağı kor bucaq (90°-dən böyük) olan üçbucağa korbucaqlı üçbucaq deyilir. Üçbucağın yalnız bir bucağı kor bucaq ola bilər. Korbucaqlı üçbucağın qalan iki bucağı iti bucaqdır.
- İki tərəfi bərabər olan üçbucağa bərabəryanlı üçbucaq deyilir.
- Tərəflərinin üçü də bərabər olan üçbucağa bərabərtərəfli (yaxud düzgün üçbucaq) deyilir. Bucaqlarının üçü də 60°-ə bərabərdir.
- Üçbucağın xarici bucaqlarının cəmi 360°-dir.
- Üçbucağın böyük bucaq qarşısındakı tərəfi kiçik bucaq qarşısındakı tərəfdən böyük olur.
- Üçbucağın hər hansı bir tərəfinin uzunluğu digər iki tərəfin uzunluqları cəmindən kiçik, fərqindən isə böyükdür (bu üçbucaq bərabərsizliyi adlanır):
- Üçbucağın tənbölənləri bir nöqtədə kəsişir.
- Üçbucağın medianları bir nöqtədə kəsişir.
Üçbucağın sahəsi


- 1-ci düstur:
![image]()
və ya
![image]()
Üçbucağın sahəsi, tərəfinin uzunluğu ilə bu tərəfə çəkilmiş olan hündürlüyü hasilinin yarısına bərabərdir.
- 2-ci düstur (Heron düsturu):
(yarımperimetr)
— Heron düsturu
- 3-cü düstur


1) 
2) 
- Əgər
üçbucağı tərəfləri
olmaqla bərabərtərəflidirsə, onda
![image]()
- Əgər
üçbucağının daxilinə çəkilmiş çevrənin radiusunu
, xaricinə çəkilmiş çevrənin radiusunu
, perimetrini isə
ilə işarə etsək, onda
1) 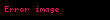
2) 
- Əgər
üçbucağı düzbucaqlı üçbucaq, katetləri isə
və
-dirsə, onda
![image]()
Üçbucağın əsas elementlərinin tapılması üçün düsturlar


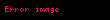






![image]()
![image]()
![image]()

Ədəbiyyat
- Riyaziyyat, qəbul imtahanlarına hazırlaşanlar, yuxarı sinif şagirdləri, və müəllimlər üçün dərs vəsaiti, M. H. Yaqubov, İ. M. Abdullayev və b. Bakı-2008.
- Cəbr-həndəsə düsturları, S. X. Rüstəmov, S. S. Rüstəmov, Z. E. Rüstəmova, Xətai kursları, Bakı-2011.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Ucbucaq Mustevinin bir duz xett uzerinde olmayan 3 noqtesini cut cut ve ardicil sekilde birlesdiren 3 duz xett parcasindan ibaret fiqur Noqteler onun tepeleri parcalar onun terefleridir Ucbucagin tepeleri adeten boyuk latin herfleri ile A B C uygun tepedeki bucaqlarin derece olcusu yunan herfleri a b g ile uygun tepenin qarsisindaki terefin uzunlugu ise elyazma latin herfleri ile a b c isare olunur Ucbucagin novleriUcbucagin novleriItibucaqli ucbucaq Korbucaqli ucbucaq Duzbucaqli ucbucaqMuxtelifterefli ucbucaq Beraberyanli ucbucaq Beraberterefli ucbucaqButun bucaqlari iti bucaq 90 dereceden kicik olan ucbucaga itibucaqli ucbucaq deyilir Bir bucagi duz bucaq 90 ye beraber olan ucbucaga duzbucaqli ucbucaq deyilir Ucbucagin yalniz bir bucagi duz bucaq ola biler Duzbucaqli ucbucagin qalan iki bucagi iti 90 den az bucaqdir Bir bucagi kor bucaq 90 den boyuk olan ucbucaga korbucaqli ucbucaq deyilir Ucbucagin yalniz bir bucagi kor bucaq ola biler Korbucaqli ucbucagin qalan iki bucagi iti bucaqdir Iki terefi beraber olan ucbucaga beraberyanli ucbucaq deyilir Tereflerinin ucu de beraber olan ucbucaga beraberterefli yaxud duzgun ucbucaq deyilir Bucaqlarinin ucu de 60 e beraberdir Ucbucagin xarici bucaqlarinin cemi 360 dir Ucbucagin boyuk bucaq qarsisindaki terefi kicik bucaq qarsisindaki terefden boyuk olur Ucbucagin her hansi bir terefinin uzunlugu diger iki terefin uzunluqlari ceminden kicik ferqinden ise boyukdur bu ucbucaq berabersizliyi adlanir b c lt a lt b c displaystyle b c lt a lt b c c a lt b lt c a textstyle c a lt b lt c a a b lt c lt a b displaystyle a b lt c lt a b Ucbucagin tenbolenleri bir noqtede kesisir Ucbucagin medianlari bir noqtede kesisir Ucbucagin sahesi ABC displaystyle triangle ABC ucbucaginin sahesi S ABC displaystyle S triangle ABC ile isare olunur 1 ci dustur S ABC 12ah displaystyle S triangle ABC 1 over 2 ah ve ya S ABC ah 2 displaystyle S triangle ABC ah 2 Ucbucagin sahesi terefinin uzunlugu ile bu terefe cekilmis olan hundurluyu hasilinin yarisina beraberdir 2 ci dustur Heron dusturu p a b c 2 displaystyle p a b c over 2 yarimperimetr S ABC p p a p b p c 14 a b c b c a a c b a b c displaystyle S triangle ABC sqrt p p a p b p c 1 over 4 square a b c b c a a c b a b c Heron dusturu 3 cu dustur S ABC displaystyle S triangle ABC de terefler a b c displaystyle a b c bu tereflerin qarsisindaki bucaqlar ise uygun olaraq a b g olarsa 1 S ABC a b sing2 displaystyle S triangle ABC frac a cdot b cdot sin gamma 2 2 S ABC a c sinb2 displaystyle S triangle ABC frac a cdot c cdot sin beta 2 Eger ABC displaystyle triangle ABC ucbucagi terefleri a displaystyle a olmaqla berabertereflidirse ondaS ABC a234 displaystyle S triangle ABC frac a 2 sqrt 3 4 Eger ABC displaystyle triangle ABC ucbucaginin daxiline cekilmis cevrenin radiusunu r displaystyle r xaricine cekilmis cevrenin radiusunu R displaystyle R perimetrini ise P displaystyle P ile isare etsek onda 1 S ABC 12Pr displaystyle S triangle ABC frac 1 2 Pr 2 S ABC abc4R displaystyle S triangle ABC frac abc 4R Eger ABC displaystyle triangle ABC ucbucagi duzbucaqli ucbucaq katetleri ise a displaystyle a ve b displaystyle b dirse ondaS ABC 12ab displaystyle S triangle ABC frac 1 2 ab Ucbucagin esas elementlerinin tapilmasi ucun dusturlar ABC displaystyle triangle ABC ucbucaginin tereflerini a b displaystyle a b ve c displaystyle c yarimperimetrini p displaystyle p p a b c2 displaystyle p frac a b c 2 a displaystyle a terefine cekilmis medianini ma displaystyle m a tenbolenini la displaystyle l a hundurluyunu ise ha displaystyle h a ile isare etsek onda la 2b cpbc p a displaystyle l a frac 2 b c sqrt pbc p a ma 122 b2 c2 a2 displaystyle m a frac 1 2 sqrt 2 b 2 c 2 a 2 ha c2 a2 c2 b22a 2 displaystyle h a sqrt c 2 frac a 2 c 2 b 2 2a 2 c displaystyle c ve b displaystyle b ni 3 cu dusturda ele yerine qoymaq lazimdir ki kokalti ifade musbet olsun EdebiyyatRiyaziyyat qebul imtahanlarina hazirlasanlar yuxari sinif sagirdleri ve muellimler ucun ders vesaiti M H Yaqubov I M Abdullayev ve b Baki 2008 Cebr hendese dusturlari S X Rustemov S S Rustemov Z E Rustemova Xetai kurslari Baki 2011
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська