Məsafə – riyaziyyat və ümumiyyətlə həyatda iki nöqtə arasındakı uzaqlığı bildirir, azərbaycan dilinə ərəbcədən keçmişdir. İki nöqtə arasındakı məsafə onları birləşdirən düz xətt parçasının uzunluğuna deyilir. İki əşya arasındakı məsafə onların bir-birinə ən yaxın yerdən birləşdirən parçanın uzunluğudur.
Kiçik məsafəni ölçmək üçün xətkeşdən istifadə edilir.
İki nöqtə Oxyz koordinat sistemində, yəni klassik Evklid həndəsəsində (fəzasında) və nöqtələri arasında müxtəlif məsafə anlayışları mövcuddur, məsələn: (birinci məsafənin adi euclidienne məsafəsidir).
| Ad | Parametr | Fonksiyon |
|---|---|---|
| Manhattan məsafəsi | 1-məsafə | |
| evklid məsafəsi | 2-məsafə | |
| Minkowski məsafəsi | p-məsafə | |
| Çebışev məsafəsi | ∞-məsafə | |
| Mahalanobis məsafəsi | statistikada | : |
və s.
Qeyri-evklid həndəsəsində məsafə adi təsəvvürdə olan məsafələrdən fərqlidir.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Mesafe riyaziyyat ve umumiyyetle heyatda iki noqte arasindaki uzaqligi bildirir azerbaycan diline erebceden kecmisdir Iki noqte arasindaki mesafe onlari birlesdiren duz xett parcasinin uzunluguna deyilir Iki esya arasindaki mesafe onlarin bir birine en yaxin yerden birlesdiren parcanin uzunlugudur Kicik mesafeni olcmek ucun xetkesden istifade edilir Iki noqte Oxyz koordinat sisteminde yeni klassik Evklid hendesesinde fezasinda A x1 y1 z1 displaystyle A x 1 y 1 z 1 ve B x2 y2 z2 displaystyle B x 2 y 2 z 2 noqteleri arasinda muxtelif mesafe anlayislari movcuddur meselen birinci mesafenin adi euclidienne mesafesidir AB x2 x1 2 y2 y1 2 z2 z1 2 displaystyle AB sqrt x 2 x 1 2 y 2 y 1 2 z 2 z 1 2 Ad Parametr FonksiyonManhattan mesafesi 1 mesafe i 1n xi yi displaystyle sum i 1 n x i y i evklid mesafesi 2 mesafe i 1n xi yi 2 displaystyle sqrt sum i 1 n x i y i 2 Minkowski mesafesi p mesafe i 1n xi yi pp displaystyle sqrt p sum i 1 n x i y i p Cebisev mesafesi mesafe limp i 1n xi yi pp supi xi yi displaystyle lim p to infty sqrt p sum i 1 n x i y i p sup i x i y i Mahalanobis mesafesi statistikada d x y x y TS 1 x y displaystyle d vec x vec y sqrt vec x vec y T S 1 vec x vec y ve s Qeyri evklid hendesesinde mesafe adi tesevvurde olan mesafelerden ferqlidir Riyaziyyat ile elaqedar bu meqale qaralama halindadir Meqaleni redakte ederek Vikipediyani zenginlesdirin Etdiyiniz redakteleri menbe ve istinadlarla esaslandirmagi unutmayin
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська


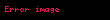
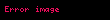

![{\displaystyle {\sqrt[{p}]{\sum _{i=1}^{n}|x_{i}-y_{i}|^{p}}}}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4ek5qQmlZelV5Tmpka05XWmtZek13TmpVeVpqUTRNMkV5Wm1ZMVlqUTFNV0kzTUdJMVl6Vmkuc3Zn.svg)
![{\displaystyle \lim _{p\to \infty }{\sqrt[{p}]{\sum _{i=1}^{n}|x_{i}-y_{i}|^{p}}}=\sup _{i}{|x_{i}-y_{i}|}}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4eVl6QXlZVE5qWkRCa016STNZalJpTUdNME1qVXlOREJpWWpoak1EVTFPVFpoWXpJM05EWm0uc3Zn.svg)
