Statistik mexanika (ing. Statistical mechanics) — mikroskopik hissəciklərin (atomlar, molekullar və s.) kollektiv davranışlarını və bu davranışların makroskopik fiziki sistemlərdə (məsələn, qazlar, bərk cisimlər, mayelər) necə təzahür etdiyini izah edən fizika sahəsi. Statistik mexanika klassik mexanika və kvant mexanikası ilə statistika və ehtimal nəzəriyyəsini birləşdirərək termodinamika qanunlarının mikroskopik əsaslarını yaradır.
Statistik mexanika, fiziki sistemin mikrohallarını nəzərə alaraq onun makroskopik davranışını proqnozlaşdırmaq məqsədi daşıyır. Bu yanaşma sayəsində entropiya, temperatur, təzyiq kimi anlayışlar molekulyar səviyyədə izah edilə bilir. Sistemlər tipik olaraq çoxlu sayda hissəcikdən ibarət olur (məsələn, 10²³ atom) və bu hissəciklərin mümkün halları statistik metodlarla təhlil olunur.
Statistik mexanika klassik termodinamikanın inkişafı nəticəsində yaranmışdır, burada temperatur, təzyiq və istilik tutumu kimi makroskopik fiziki xassələri orta dəyərlər ətrafında dəyişən və ehtimal paylamaları ilə xarakterizə olunan mikroskopik parametrlər baxımından uğurla izah etmişdir.
Klassik termodinamika ilk növbədə termodinamik tarazlıqla məşğul olduğu halda, qeyri-tarazlıq statistik mexanikasında disbalansın səbəb olduğu dönməz proseslərin sürətlərinin mikroskopik modelləşdirilməsi suallarına tətbiq edilir. Belə proseslərə misal olaraq kimyəvi reaksiyalar, hissəcik axınları və istilik axınlarını göstərmək olar. Fluktuasiya-dissipasiya teoremi çoxlu hissəciklərdən ibarət sistemdə stasionar cərəyanın ən sadə qeyri-tarazlıq vəziyyətinin öyrənilməsi üçün qeyri-tarazlıq statistik mexanikasının tətbiqi ilə əldə edilən əsas bilikdir.
Tarixi
Statistik mexanikanın tarixi XIX əsrin ortalarından başlayaraq klassik mexanika və termodinamika arasında körpü qurmaq cəhdləri ilə formalaşmağa başlamışdır. Bu sahənin inkişafı əsasən qazların davranışlarını və mikroskopik əsaslarını anlamaq məqsədilə aparılan tədqiqatlarla əlaqəlidir.Rudolf Klauzius, Ceyms Klark Maksvell və Lüdviq Bolsman kimi alimlər inkişaf etdirdilər. Bu nəzəriyyəyə əsasən, qazlar çoxlu sayda hissəcikdən ibarətdir və onların təsadüfi hərəkəti nəticəsində təzyiq və temperatur kimi makroskopik dəyişənlər yaranır. Maksvell 1860-cı illərdə qaz molekullarının sürət paylanmasını (Maksvel paylanması) təqdim etdi. Bolsman isə entropiya anlayışını mikroskopik səviyyədə izah etməyə çalışdı və onun məşhur S = k log W düsturu entropiyanın statistik mənasını verdi.

Cozayya Uillard Gibbs statistik mexanikanın riyazi əsaslarını formalaşdırdı. O, təqdim edərək müxtəlif fiziki sistemlərin termodinamik parametrlərini izah edən statistika toplusunu müəyyənləşdirdi (mikrokanyonik, kanonik və böyük kanonik ansambl). Gibbsin 1902-ci ildə nəşr etdiyi “Elementary Principles in Statistical Mechanics” əsəri sahənin əsas təməl kitabı sayılır. Bolsmanın dövründə onun statistik entropiya yanaşması elmi ictimaiyyət tərəfindən geniş şəkildə qəbul edilməmişdi. Xüsusilə Ernst Zermelo və digərləri Puankare əksərilik teoreminə əsaslanaraq entropiyanın artım qanununa şübhə ilə yanaşırdılar. Bolsman 1906-cı ildə vəfat etdikdən sonra onun ideyaları geniş şəkildə qəbul olunmağa başladı.
XX əsrin əvvəllərində kvant mexanikasının formalaşması ilə statistik mexanika yeni istiqamətlərə yönəldi.Albert Eynşteyn və Satyendra Nat Bose tərəfindən 1924-cü ildə təqdim edildi. Enriko Fermi və Pol Dirak isə Fermi–Dirak statistikasını formalaşdıraraq fermionların davranışını izah etdilər. Bu statistikalar sayəsində aşağı temperaturda və yüksək sıxlıqlı sistemlərin mikroskopik davranışı anlaşıldı. Statistik mexanika qraf nəzəriyyəsi, və faza keçidləri kimi sahələrdə mühüm rol oynadı. Lev Landau faza keçidlərinin nəzəri modelini yaratdı və bu model daha sonra yanaşması ilə zənginləşdirildi. , və maddənin maqnetik və istilik xassələrini izah etməkdə istifadə olundu. XX əsrin sonu və XXI əsrin əvvəllərində statistik mexanika , , və kimi yeni sahələrdə tətbiq olunmağa başladı. və metodları statistik mexanikanın tətbiqini genişləndirdi. Eyni zamanda ilə statistik mexanika arasında əlaqələr araşdırılır. Statistik mexanika həm fundamental fizikanın əsas dayağı, həm də real sistemlərin davranışını izah edən praktik vasitə kimi elm tarixində öz əhəmiyyətli yerini qoruyur. Onun inkişafı termodinamika, kvant fizikası, materialşünaslıq və biologiya kimi sahələrə töhfə vermişdir.
Statistik termodinamika
Statistik termodinamika (ing. Statistical thermodynamics) — statistik mexanika və termodinamikanın birləşməsindən yaranan elmi sahə. O, fiziki sistemlərin makroskopik xassələrini (məsələn, temperatur, təzyiq, entalpiya, entropiya) onların mikroskopik quruluşuna və hissəciklərin statistik davranışına əsaslanaraq izah edir. Bu sahə, xüsusilə termodinamik qanunların mənşəyini anlamağa imkan verir.
Fundamental postulat
Statistik termodinamikanın əsas postulatı ondan ibarətdir ki, verilmiş üçün uyğun gələn bütün bərabər ehtimalla baş verə bilər. Bu postulatdan çıxış edərək makroskopik dəyişənlərin orta qiymətləri hesablana bilər. Bu yanaşma vasitəsilə, və digər müşahidə olunan dəyərlər mikroskopik dəyişənlərin ehtimal paylanmaları ilə ifadə olunur.
Üç əsas termodinamik ansambl
Statistik termodinamika müxtəlif şərtlər üçün fərqli istifadə edir. Əsas ansambl növləri aşağıdakılardır:
- Mikrokanyonik ansambl (NVE) — enerji, hissəcik sayı və həcmi sabit olan sistemlər üçün istifadə olunur.
- Kanonik ansambl (NVT) — temperatur, hissəcik sayı və həcmi sabit qalır. Bu ansambl istilik hamamı ilə enerji mübadiləsi edən sistemlər üçün uyğundur.
- Böyük kanonik ansambl (µVT) — temperatur, kimyəvi potensial və həcmi sabit qalmaqla hissəcik sayı dəyişə bilər. Bu ansambl açıq sistemlərin modelləşdirilməsi üçün uyğundur.
| Sabit dəyişənlər |  |  |  |
|---|---|---|---|
| Mikroskopik xüsusiyyətlər | sayı | ||
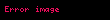 |  |  | |
| Makroskopik funksiya | |||
 |  |  |
Hesablama üsulları
Verilmiş sistem üçün ansambl hal xarakteristikası funksiyası hesablandıqdan sonra sistemin “həll edildiyi” deyilir (makroskopik müşahidə olunanlar hal xarakteristika funksiyasından çıxarıla bilər). Bununla belə, termodinamik ansamblın hal xarakteristikası funksiyasının hesablanması həmişə asan məsələ deyil, çünki sistemin bütün mümkün vəziyyətlərini nəzərə almaq lazımdır. Bəzi fərziyyə sistemləri tam olaraq həll olunsa da, ən ümumi (və real) vəziyyət dəqiq həll oluna bilməyəcək qədər mürəkkəbdir. Həqiqi ansamblı təxmin etmək və ortalamaları hesablamaq üçün müxtəlif yanaşmalar mövcuddur.
Dəqiq metodlar
Sadə sistemlər üçün mikrohaların tam sayını hesablamaqla bütün termodinamik funksiyalar analitik şəkildə əldə edilə bilər. Məsələn:
- (1 ölçülü hal üçün)
Monte-Karlo üsulları
Çoxlu mikrohalları təsadüfi üsullarla nümunə götürərək statistik təxmini nəticələr əldə etməyə əsaslanan güclü rəqəmsal yanaşmadır. Xüsusilə mürəkkəb və yüksəkölçülü sistemlər üçün effektivdir. bu sahədə ən geniş yayılmış texnikadır.
Tarazlıqda olmayan statistik mexanika
Tarazlıq vəziyyətindən uzaq olan sistemlərin davranışlarını izah etmək üçün statistik termodinamikanın qeyri-tarazlıq formaları inkişaf etdirilmişdir. Prinsip etibarilə, qeyri-tarazlıq statistik mexanika riyazi baxımdan tam dəqiq şəkildə ifadə oluna bilər. Təcrid olunmuş sistemlər üçün statistik ansamblın zamanla inkişafı və ya onun kvant analoqu olan ilə təsvir edilir. Bu tənliklər, sistemin mikrohallarının hər birinə uyğun olaraq klassik mexanika və ya kvant mexanikası qanunlarının tətbiqi nəticəsində əldə olunur.
Ansamblın təkamül tənlikləri sistemin əsas hərəkət qanunlarının mürəkkəbliyini əks etdirir və bu səbəbdən onların dəqiq analitik həlləri, ümumilikdə, çox çətindir. Bundan əlavə, bu tənliklər tərsinə çevriləbiləndir və prinsipi ilə işləyir — yəni zamanla sabit qalır və sistemin dinamikasında informasiya itmir.
Lakin real sistemlərdə müşahidə olunan modelləşdirilməsi üçün bu deterministik yanaşma kifayət etmir. Belə hallarda, ehtimala əsaslanan əlavə mexanizmlərin və ilə yanaşı, kimi müşahidə olunan makroskopik xüsusiyyətlərin izahı üçün əlavə statistik və ya fenomenoloji modellərin tətbiqi zəruri olur.
İstinadlar
- Teschendorff, Andrew E.; Feinberg, Andrew P. "Statistical mechanics meets single-cell biology". Nature Reviews Genetics. 22 (7). July 2021: 459–476. doi:10.1038/s41576-021-00341-z. PMC 10152720 (#bad_pmc). PMID 33875884 (#bad_pmid).
- Advani, Madhu; Lahiri, Subhaneil; Ganguli, Surya. "Statistical mechanics of complex neural systems and high dimensional data". Journal of Statistical Mechanics: Theory and Experiment. 2013 (3). 12 March 2013: P03014. arXiv:1301.7115. Bibcode:2013JSMTE..03..014A. doi:10.1088/1742-5468/2013/03/P03014.
- Huang, Haiping. Statistical Mechanics of Neural Networks. 2021. doi:10.1007/978-981-16-7570-6. ISBN .
- Berger, Adam L.; Pietra, Vincent J. Della; Pietra, Stephen A. Della. "A maximum entropy approach to natural language processing" (PDF). Computational Linguistics. 22 (1). March 1996: 39–71. .
- Jaynes, E. T. "Information Theory and Statistical Mechanics". Physical Review. 106 (4). 15 May 1957: 620–630. Bibcode:1957PhRv..106..620J. doi:10.1103/PhysRev.106.620.
- Durlauf, Steven N. "How can statistical mechanics contribute to social science?". Proceedings of the National Academy of Sciences. 96 (19). 14 September 1999: 10582–10584. Bibcode:1999PNAS...9610582D. doi:10.1073/pnas.96.19.10582. PMC 33748. PMID 10485867.
- Huang, Kerson. Introduction to Statistical Physics (2nd). CRC Press. 2009-09-21. səh. 15. ISBN .
- Germano, R. Física Estatística do Equilíbrio: um curso introdutório (Portuguese). Rio de Janeiro: Ciência Moderna. 2022. səh. 156. ISBN .
- Reif, Frederick. Fundamentals of Statistical and Thermal Physics. McGraw–Hill. 1965. 651. ISBN .
- Mahon, Basil. The Man Who Changed Everything – the Life of James Clerk Maxwell. Hoboken, NJ: Wiley. 2003. ISBN . OCLC 52358254.
- Gyenis, Balazs. "Maxwell and the normal distribution: A colored story of probability, independence, and tendency towards equilibrium". Studies in History and Philosophy of Modern Physics. 57. 2017: 53–65. arXiv:1702.01411. Bibcode:2017SHPMP..57...53G. doi:10.1016/j.shpsb.2017.01.001.
- James Clerk Maxwell ,Theory of Heat (London, England: Longmans, Green, and Co., 1871), p. 309
- Mayants, Lazar. The enigma of probability and physics. Springer. 1984. səh. 174. ISBN .
- Gibbs, J. W. On the Fundamental Formula of Statistical Mechanics, with Applications to Astronomy and Thermodynamics. 1885. OCLC 702360353.
- Jaynes, E. "Information Theory and Statistical Mechanics". Physical Review. 106 (4). 1957: 620–630. Bibcode:1957PhRv..106..620J. doi:10.1103/PhysRev.106.620.
- Gao, Xiang; Gallicchio, Emilio; Roitberg, Adrian E. "The generalized Boltzmann distribution is the only distribution in which the Gibbs-Shannon entropy equals the thermodynamic entropy". The Journal of Chemical Physics. 151 (3). 21 July 2019: 034113. arXiv:1903.02121. Bibcode:2019JChPh.151c4113G. doi:10.1063/1.5111333. PMID 31325924.
- Gao, Xiang. "The Mathematics of the Ensemble Theory". Results in Physics. 34. March 2022: 105230. arXiv:2006.00485. Bibcode:2022ResPh..3405230G. doi:10.1016/j.rinp.2022.105230.
- The Concentration of Measure Phenomenon (PDF). Mathematical Surveys and Monographs. 89. 2005. doi:10.1090/surv/089. ISBN .
- Touchette, Hugo. "Equivalence and Nonequivalence of Ensembles: Thermodynamic, Macrostate, and Measure Levels". Journal of Statistical Physics. 159 (5). 2015: 987–1016. arXiv:1403.6608. Bibcode:2015JSP...159..987T. doi:10.1007/s10955-015-1212-2.
- Gorban, A. N.; Tyukin, I. Y. "Blessing of dimensionality: mathematical foundations of the statistical physics of data". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 376 (2118). 28 April 2018: 20170237. arXiv:1801.03421. Bibcode:2018RSPTA.37670237G. doi:10.1098/rsta.2017.0237. PMC 5869543. PMID 29555807.
- Baxter, Rodney J. Exactly solved models in statistical mechanics. Academic Press Inc. 1982. ISBN .
- Jia, Xun; Ziegenhein, Peter; Jiang, Steve B. "GPU-based high-performance computing for radiation therapy". Physics in Medicine and Biology. 59 (4). 2014: R151–R182. Bibcode:2014PMB....59R.151J. doi:10.1088/0031-9155/59/4/R151. PMC 4003902. PMID 24486639.
- Hill, R; Healy, B; Holloway, L; Kuncic, Z; Thwaites, D; Baldock, C. "Advances in kilovoltage x-ray beam dosimetry". Physics in Medicine and Biology. 59 (6). Mar 2014: R183–R231. Bibcode:2014PMB....59R.183H. doi:10.1088/0031-9155/59/6/R183. PMID 24584183.
- Rogers, D W O. "Fifty years of Monte Carlo simulations for medical physics". Physics in Medicine and Biology. 51 (13). 2006: R287–R301. Bibcode:2006PMB....51R.287R. doi:10.1088/0031-9155/51/13/R17. PMID 16790908.
- Gibbs, Josiah Willard. Elementary Principles in Statistical Mechanics. New York: Charles Scribner's Sons. 1902.
- Altshuler, B L; Aronov, A G; Khmelnitsky, D E. "Effects of electron-electron collisions with small energy transfers on quantum localisation". Journal of Physics C: Solid State Physics. 15 (36). 30 December 1982: 7367–7386. Bibcode:1982JPhC...15.7367A. doi:10.1088/0022-3719/15/36/018.
- Aleiner, I. L.; Blanter, Ya. M. "Inelastic scattering time for conductance fluctuations". Physical Review B. 65 (11). 28 February 2002: 115317. arXiv:cond-mat/0105436. Bibcode:2002PhRvB..65k5317A. doi:10.1103/PhysRevB.65.115317.
- Ramezanpour, Abolfazl; Beam, Andrew L.; Chen, Jonathan H.; Mashaghi, Alireza. "Statistical Physics for Medical Diagnostics: Learning, Inference, and Optimization Algorithms". Diagnostics. 10 (11). 19 November 2020: 972. doi:10.3390/diagnostics10110972. PMC 7699346 (#bad_pmc). PMID 33228143 (#bad_pmid).
- Mashaghi, Alireza; Ramezanpour, Abolfazl. "Statistical physics of medical diagnostics: Study of a probabilistic model". Physical Review E. 97 (3). 16 March 2018: 032118. arXiv:1803.10019. Bibcode:2018PhRvE..97c2118M. doi:10.1103/PhysRevE.97.032118. PMID 29776109.
- Uffink, Jos. Compendium of the foundations of classical statistical physics (Preprint). March 2006.
- Balescu, Radu. Equilibrium and Non-Equilibrium Statistical Mechanics. Wiley. 1975. ISBN .
Əlavə ədəbiyyat
- Reif, F. Fundamentals of Statistical and Thermal Physics. Waveland Press. 2009. ISBN .
- Müller-Kirsten, Harald J W. Basics of Statistical Physics (PDF). 2013. doi:10.1142/8709. ISBN .
- Kadanoff, Leo P. "Statistical Physics and other resources". August 12, 2021 tarixində orijinalından arxivləşdirilib. İstifadə tarixi: June 18, 2023.
- Kadanoff, Leo P. Statistical Physics: Statics, Dynamics and Renormalization. World Scientific. 2000. ISBN .
- Flamm, Dieter. "History and outlook of statistical physics". 1998. arXiv:physics/9803005.
Xarici keçidlər
- Philosophy of Statistical Mechanics article by Lawrence Sklar for the Stanford Encyclopedia of Philosophy.
- Sklogwiki - Thermodynamics, statistical mechanics, and the computer simulation of materials. SklogWiki is particularly oriented towards liquids and soft condensed matter.
- Thermodynamics and Statistical Mechanics by Richard Fitzpatrick
- Cohen, Doron. "Lecture Notes in Statistical Mechanics and Mesoscopics". 2011. arXiv:1107.0568 [quant-ph].
- Videos of lecture series in statistical mechanics — YouTube platformasında taught by Leonard Susskind.
- Vu-Quoc, L., Configuration integral (statistical mechanics), 2008. This wiki site is down; see this article in the web archive on 2012 April 28.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Statistik mexanika ing Statistical mechanics mikroskopik hisseciklerin atomlar molekullar ve s kollektiv davranislarini ve bu davranislarin makroskopik fiziki sistemlerde meselen qazlar berk cisimler mayeler nece tezahur etdiyini izah eden fizika sahesi Statistik mexanika klassik mexanika ve kvant mexanikasi ile statistika ve ehtimal nezeriyyesini birlesdirerek termodinamika qanunlarinin mikroskopik esaslarini yaradir Statistik mexanika fiziki sistemin mikrohallarini nezere alaraq onun makroskopik davranisini proqnozlasdirmaq meqsedi dasiyir Bu yanasma sayesinde entropiya temperatur tezyiq kimi anlayislar molekulyar seviyyede izah edile bilir Sistemler tipik olaraq coxlu sayda hissecikden ibaret olur meselen 10 atom ve bu hisseciklerin mumkun hallari statistik metodlarla tehlil olunur Statistik mexanika klassik termodinamikanin inkisafi neticesinde yaranmisdir burada temperatur tezyiq ve istilik tutumu kimi makroskopik fiziki xasseleri orta deyerler etrafinda deyisen ve ehtimal paylamalari ile xarakterize olunan mikroskopik parametrler baximindan ugurla izah etmisdir Klassik termodinamika ilk novbede termodinamik tarazliqla mesgul oldugu halda qeyri tarazliq statistik mexanikasinda disbalansin sebeb oldugu donmez proseslerin suretlerinin mikroskopik modellesdirilmesi suallarina tetbiq edilir Bele proseslere misal olaraq kimyevi reaksiyalar hissecik axinlari ve istilik axinlarini gostermek olar Fluktuasiya dissipasiya teoremi coxlu hisseciklerden ibaret sistemde stasionar cereyanin en sade qeyri tarazliq veziyyetinin oyrenilmesi ucun qeyri tarazliq statistik mexanikasinin tetbiqi ile elde edilen esas bilikdir TarixiStatistik mexanikanin tarixi XIX esrin ortalarindan baslayaraq klassik mexanika ve termodinamika arasinda korpu qurmaq cehdleri ile formalasmaga baslamisdir Bu sahenin inkisafi esasen qazlarin davranislarini ve mikroskopik esaslarini anlamaq meqsedile aparilan tedqiqatlarla elaqelidir Rudolf Klauzius Ceyms Klark Maksvell ve Ludviq Bolsman kimi alimler inkisaf etdirdiler Bu nezeriyyeye esasen qazlar coxlu sayda hissecikden ibaretdir ve onlarin tesadufi hereketi neticesinde tezyiq ve temperatur kimi makroskopik deyisenler yaranir Maksvell 1860 ci illerde qaz molekullarinin suret paylanmasini Maksvel paylanmasi teqdim etdi Bolsman ise entropiya anlayisini mikroskopik seviyyede izah etmeye calisdi ve onun meshur S k log W dusturu entropiyanin statistik menasini verdi Cozayya Uillard Gibbsin Elementary Principles in Statistical Mechanics eseri Cozayya Uillard Gibbs statistik mexanikanin riyazi esaslarini formalasdirdi O teqdim ederek muxtelif fiziki sistemlerin termodinamik parametrlerini izah eden statistika toplusunu mueyyenlesdirdi mikrokanyonik kanonik ve boyuk kanonik ansambl Gibbsin 1902 ci ilde nesr etdiyi Elementary Principles in Statistical Mechanics eseri sahenin esas temel kitabi sayilir Bolsmanin dovrunde onun statistik entropiya yanasmasi elmi ictimaiyyet terefinden genis sekilde qebul edilmemisdi Xususile Ernst Zermelo ve digerleri Puankare ekserilik teoremine esaslanaraq entropiyanin artim qanununa subhe ile yanasirdilar Bolsman 1906 ci ilde vefat etdikden sonra onun ideyalari genis sekilde qebul olunmaga basladi XX esrin evvellerinde kvant mexanikasinin formalasmasi ile statistik mexanika yeni istiqametlere yoneldi Albert Eynsteyn ve Satyendra Nat Bose terefinden 1924 cu ilde teqdim edildi Enriko Fermi ve Pol Dirak ise Fermi Dirak statistikasini formalasdiraraq fermionlarin davranisini izah etdiler Bu statistikalar sayesinde asagi temperaturda ve yuksek sixliqli sistemlerin mikroskopik davranisi anlasildi Statistik mexanika qraf nezeriyyesi ve faza kecidleri kimi sahelerde muhum rol oynadi Lev Landau faza kecidlerinin nezeri modelini yaratdi ve bu model daha sonra yanasmasi ile zenginlesdirildi ve maddenin maqnetik ve istilik xasselerini izah etmekde istifade olundu XX esrin sonu ve XXI esrin evvellerinde statistik mexanika ve kimi yeni sahelerde tetbiq olunmaga basladi ve metodlari statistik mexanikanin tetbiqini genislendirdi Eyni zamanda ile statistik mexanika arasinda elaqeler arasdirilir Statistik mexanika hem fundamental fizikanin esas dayagi hem de real sistemlerin davranisini izah eden praktik vasite kimi elm tarixinde oz ehemiyyetli yerini qoruyur Onun inkisafi termodinamika kvant fizikasi materialsunasliq ve biologiya kimi sahelere tohfe vermisdir Statistik termodinamikaStatistik termodinamika ing Statistical thermodynamics statistik mexanika ve termodinamikanin birlesmesinden yaranan elmi sahe O fiziki sistemlerin makroskopik xasselerini meselen temperatur tezyiq entalpiya entropiya onlarin mikroskopik qurulusuna ve hisseciklerin statistik davranisina esaslanaraq izah edir Bu sahe xususile termodinamik qanunlarin menseyini anlamaga imkan verir Fundamental postulat Statistik termodinamikanin esas postulati ondan ibaretdir ki verilmis ucun uygun gelen butun beraber ehtimalla bas vere biler Bu postulatdan cixis ederek makroskopik deyisenlerin orta qiymetleri hesablana biler Bu yanasma vasitesile ve diger musahide olunan deyerler mikroskopik deyisenlerin ehtimal paylanmalari ile ifade olunur Uc esas termodinamik ansambl Statistik termodinamika muxtelif sertler ucun ferqli istifade edir Esas ansambl novleri asagidakilardir Mikrokanyonik ansambl NVE enerji hissecik sayi ve hecmi sabit olan sistemler ucun istifade olunur Kanonik ansambl NVT temperatur hissecik sayi ve hecmi sabit qalir Bu ansambl istilik hamami ile enerji mubadilesi eden sistemler ucun uygundur Boyuk kanonik ansambl µVT temperatur kimyevi potensial ve hecmi sabit qalmaqla hissecik sayi deyise biler Bu ansambl aciq sistemlerin modellesdirilmesi ucun uygundur Termodinamik ansambllar Sabit deyisenler E N V displaystyle E N V T N V displaystyle T N V T m V displaystyle T mu V Mikroskopik xususiyyetler sayiW displaystyle W Z ke Ek kBT displaystyle Z sum k e E k k B T Z ke Ek mNk kBT displaystyle mathcal Z sum k e E k mu N k k B T Makroskopik funksiyaS kBlog W displaystyle S k B log W F kBTlog Z displaystyle F k B T log Z W kBTlog Z displaystyle Omega k B T log mathcal Z Hesablama usullari Verilmis sistem ucun ansambl hal xarakteristikasi funksiyasi hesablandiqdan sonra sistemin hell edildiyi deyilir makroskopik musahide olunanlar hal xarakteristika funksiyasindan cixarila biler Bununla bele termodinamik ansamblin hal xarakteristikasi funksiyasinin hesablanmasi hemise asan mesele deyil cunki sistemin butun mumkun veziyyetlerini nezere almaq lazimdir Bezi ferziyye sistemleri tam olaraq hell olunsa da en umumi ve real veziyyet deqiq hell oluna bilmeyecek qeder murekkebdir Heqiqi ansambli texmin etmek ve ortalamalari hesablamaq ucun muxtelif yanasmalar movcuddur Deqiq metodlar Sade sistemler ucun mikrohalarin tam sayini hesablamaqla butun termodinamik funksiyalar analitik sekilde elde edile biler Meselen 1 olculu hal ucun Monte Karlo usullari Coxlu mikrohallari tesadufi usullarla numune goturerek statistik texmini neticeler elde etmeye esaslanan guclu reqemsal yanasmadir Xususile murekkeb ve yuksekolculu sistemler ucun effektivdir bu sahede en genis yayilmis texnikadir Tarazliqda olmayan statistik mexanikaTarazliq veziyyetinden uzaq olan sistemlerin davranislarini izah etmek ucun statistik termodinamikanin qeyri tarazliq formalari inkisaf etdirilmisdir Prinsip etibarile qeyri tarazliq statistik mexanika riyazi baximdan tam deqiq sekilde ifade oluna biler Tecrid olunmus sistemler ucun statistik ansamblin zamanla inkisafi ve ya onun kvant analoqu olan ile tesvir edilir Bu tenlikler sistemin mikrohallarinin her birine uygun olaraq klassik mexanika ve ya kvant mexanikasi qanunlarinin tetbiqi neticesinde elde olunur Ansamblin tekamul tenlikleri sistemin esas hereket qanunlarinin murekkebliyini eks etdirir ve bu sebebden onlarin deqiq analitik helleri umumilikde cox cetindir Bundan elave bu tenlikler tersine cevrilebilendir ve prinsipi ile isleyir yeni zamanla sabit qalir ve sistemin dinamikasinda informasiya itmir Lakin real sistemlerde musahide olunan modellesdirilmesi ucun bu deterministik yanasma kifayet etmir Bele hallarda ehtimala esaslanan elave mexanizmlerin ve ile yanasi kimi musahide olunan makroskopik xususiyyetlerin izahi ucun elave statistik ve ya fenomenoloji modellerin tetbiqi zeruri olur IstinadlarTeschendorff Andrew E Feinberg Andrew P Statistical mechanics meets single cell biology Nature Reviews Genetics 22 7 July 2021 459 476 doi 10 1038 s41576 021 00341 z PMC 10152720 bad pmc PMID 33875884 bad pmid Advani Madhu Lahiri Subhaneil Ganguli Surya Statistical mechanics of complex neural systems and high dimensional data Journal of Statistical Mechanics Theory and Experiment 2013 3 12 March 2013 P03014 arXiv 1301 7115 Bibcode 2013JSMTE 03 014A doi 10 1088 1742 5468 2013 03 P03014 Huang Haiping Statistical Mechanics of Neural Networks 2021 doi 10 1007 978 981 16 7570 6 ISBN 978 981 16 7569 0 Berger Adam L Pietra Vincent J Della Pietra Stephen A Della A maximum entropy approach to natural language processing PDF Computational Linguistics 22 1 March 1996 39 71 Jaynes E T Information Theory and Statistical Mechanics Physical Review 106 4 15 May 1957 620 630 Bibcode 1957PhRv 106 620J doi 10 1103 PhysRev 106 620 Durlauf Steven N How can statistical mechanics contribute to social science Proceedings of the National Academy of Sciences 96 19 14 September 1999 10582 10584 Bibcode 1999PNAS 9610582D doi 10 1073 pnas 96 19 10582 PMC 33748 PMID 10485867 Huang Kerson Introduction to Statistical Physics 2nd CRC Press 2009 09 21 seh 15 ISBN 978 1 4200 7902 9 Germano R Fisica Estatistica do Equilibrio um curso introdutorio Portuguese Rio de Janeiro Ciencia Moderna 2022 seh 156 ISBN 978 65 5842 144 3 Reif Frederick Fundamentals of Statistical and Thermal Physics McGraw Hill 1965 651 ISBN 978 0 07 051800 1 Mahon Basil The Man Who Changed Everything the Life of James Clerk Maxwell Hoboken NJ Wiley 2003 ISBN 978 0 470 86171 4 OCLC 52358254 Gyenis Balazs Maxwell and the normal distribution A colored story of probability independence and tendency towards equilibrium Studies in History and Philosophy of Modern Physics 57 2017 53 65 arXiv 1702 01411 Bibcode 2017SHPMP 57 53G doi 10 1016 j shpsb 2017 01 001 James Clerk Maxwell Theory of Heat London England Longmans Green and Co 1871 p 309 Mayants Lazar The enigma of probability and physics Springer 1984 seh 174 ISBN 978 90 277 1674 3 Gibbs J W On the Fundamental Formula of Statistical Mechanics with Applications to Astronomy and Thermodynamics 1885 OCLC 702360353 Jaynes E Information Theory and Statistical Mechanics Physical Review 106 4 1957 620 630 Bibcode 1957PhRv 106 620J doi 10 1103 PhysRev 106 620 Gao Xiang Gallicchio Emilio Roitberg Adrian E The generalized Boltzmann distribution is the only distribution in which the Gibbs Shannon entropy equals the thermodynamic entropy The Journal of Chemical Physics 151 3 21 July 2019 034113 arXiv 1903 02121 Bibcode 2019JChPh 151c4113G doi 10 1063 1 5111333 PMID 31325924 Gao Xiang The Mathematics of the Ensemble Theory Results in Physics 34 March 2022 105230 arXiv 2006 00485 Bibcode 2022ResPh 3405230G doi 10 1016 j rinp 2022 105230 The Concentration of Measure Phenomenon PDF Mathematical Surveys and Monographs 89 2005 doi 10 1090 surv 089 ISBN 978 0 8218 3792 4 Touchette Hugo Equivalence and Nonequivalence of Ensembles Thermodynamic Macrostate and Measure Levels Journal of Statistical Physics 159 5 2015 987 1016 arXiv 1403 6608 Bibcode 2015JSP 159 987T doi 10 1007 s10955 015 1212 2 Gorban A N Tyukin I Y Blessing of dimensionality mathematical foundations of the statistical physics of data Philosophical Transactions of the Royal Society A Mathematical Physical and Engineering Sciences 376 2118 28 April 2018 20170237 arXiv 1801 03421 Bibcode 2018RSPTA 37670237G doi 10 1098 rsta 2017 0237 PMC 5869543 PMID 29555807 Baxter Rodney J Exactly solved models in statistical mechanics Academic Press Inc 1982 ISBN 978 0 12 083180 7 Jia Xun Ziegenhein Peter Jiang Steve B GPU based high performance computing for radiation therapy Physics in Medicine and Biology 59 4 2014 R151 R182 Bibcode 2014PMB 59R 151J doi 10 1088 0031 9155 59 4 R151 PMC 4003902 PMID 24486639 Hill R Healy B Holloway L Kuncic Z Thwaites D Baldock C Advances in kilovoltage x ray beam dosimetry Physics in Medicine and Biology 59 6 Mar 2014 R183 R231 Bibcode 2014PMB 59R 183H doi 10 1088 0031 9155 59 6 R183 PMID 24584183 Rogers D W O Fifty years of Monte Carlo simulations for medical physics Physics in Medicine and Biology 51 13 2006 R287 R301 Bibcode 2006PMB 51R 287R doi 10 1088 0031 9155 51 13 R17 PMID 16790908 Gibbs Josiah Willard Elementary Principles in Statistical Mechanics New York Charles Scribner s Sons 1902 Altshuler B L Aronov A G Khmelnitsky D E Effects of electron electron collisions with small energy transfers on quantum localisation Journal of Physics C Solid State Physics 15 36 30 December 1982 7367 7386 Bibcode 1982JPhC 15 7367A doi 10 1088 0022 3719 15 36 018 Aleiner I L Blanter Ya M Inelastic scattering time for conductance fluctuations Physical Review B 65 11 28 February 2002 115317 arXiv cond mat 0105436 Bibcode 2002PhRvB 65k5317A doi 10 1103 PhysRevB 65 115317 Ramezanpour Abolfazl Beam Andrew L Chen Jonathan H Mashaghi Alireza Statistical Physics for Medical Diagnostics Learning Inference and Optimization Algorithms Diagnostics 10 11 19 November 2020 972 doi 10 3390 diagnostics10110972 PMC 7699346 bad pmc PMID 33228143 bad pmid Mashaghi Alireza Ramezanpour Abolfazl Statistical physics of medical diagnostics Study of a probabilistic model Physical Review E 97 3 16 March 2018 032118 arXiv 1803 10019 Bibcode 2018PhRvE 97c2118M doi 10 1103 PhysRevE 97 032118 PMID 29776109 Uffink Jos Compendium of the foundations of classical statistical physics Preprint March 2006 Balescu Radu Equilibrium and Non Equilibrium Statistical Mechanics Wiley 1975 ISBN 978 0 471 04600 4 Elave edebiyyatReif F Fundamentals of Statistical and Thermal Physics Waveland Press 2009 ISBN 978 1 4786 1005 2 Muller Kirsten Harald J W Basics of Statistical Physics PDF 2013 doi 10 1142 8709 ISBN 978 981 4449 53 3 Kadanoff Leo P Statistical Physics and other resources August 12 2021 tarixinde orijinalindan arxivlesdirilib Istifade tarixi June 18 2023 Kadanoff Leo P Statistical Physics Statics Dynamics and Renormalization World Scientific 2000 ISBN 978 981 02 3764 6 Flamm Dieter History and outlook of statistical physics 1998 arXiv physics 9803005 Xarici kecidlerVikianbarda Statistik mexanika ile elaqeli mediafayllar var Philosophy of Statistical Mechanics article by Lawrence Sklar for the Stanford Encyclopedia of Philosophy Sklogwiki Thermodynamics statistical mechanics and the computer simulation of materials SklogWiki is particularly oriented towards liquids and soft condensed matter Thermodynamics and Statistical Mechanics by Richard Fitzpatrick Cohen Doron Lecture Notes in Statistical Mechanics and Mesoscopics 2011 arXiv 1107 0568 quant ph Videos of lecture series in statistical mechanics YouTube platformasinda taught by Leonard Susskind Vu Quoc L Configuration integral statistical mechanics 2008 This wiki site is down see this article in the web archive on 2012 April 28
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State
