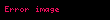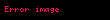Lopital qaydası (teoremi) (həmçinin Bernulli — Lopital qaydası ) — funksiyaların limitinin tapılması metodudur. Bu metod ən çox və qeyri-müəyyənliklərinin tapılmasında istifadə olunur. Metodu əsaslandıran teorem iddia edir ki, bəzi şərtlərdə funksiyaların əlaqəsinin limiti onların törəmələri limitinə bərabərdir.
Dəqiq qısa fikir
Lopital teoremi:
;
və
---
ətrafında differensiallaşdırır;
---
-nın ətrafında təyin olunur;
olur,
onda 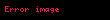
Limitlər həmçinin birtərəfli ola bilər.
Tarix
Qeyri-müəyyənliklərin bu cür açılış üsulu 1696-cı ildə müəllifi Giyom Lopital olan "Analyse des Infiniment Petits" dərsliyində dərc edilmişdi. Metodu ilk kəşf edən İohan Bernulli məktubunda Lopitala bu haqda bildirmişdi.
Mənbə
- "Arxivlənmiş surət" (PDF). 2009-02-06 tarixində (PDF). İstifadə tarixi: 2013-11-26.
- Paul J. Nahin, An Imaginary Tale: The Story of
, p.216
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Lopital qaydasi teoremi hemcinin Bernulli Lopital qaydasi funksiyalarin limitinin tapilmasi metodudur Bu metod en cox 0 0 displaystyle 0 0 ve displaystyle infty infty qeyri mueyyenliklerinin tapilmasinda istifade olunur Metodu esaslandiran teorem iddia edir ki bezi sertlerde funksiyalarin elaqesinin limiti onlarin toremeleri limitine beraberdir Deqiq qisa fikirLopital teoremi limx af x limx ag x 0ve ya displaystyle lim x to a f x lim x to a g x 0 operatorname ve ya infty f x displaystyle f x ve g x displaystyle g x a displaystyle a etrafinda differensiallasdirir g x 0 displaystyle g x neq 0 a displaystyle a nin etrafinda teyin olunur limx af x g x displaystyle lim x to a frac f x g x olur onda limx af x g x limx af x g x displaystyle lim x to a frac f x g x lim x to a frac f x g x olar Limitler hemcinin birterefli ola biler TarixQeyri mueyyenliklerin bu cur acilis usulu 1696 ci ilde muellifi Giyom Lopital olan Analyse des Infiniment Petits dersliyinde derc edilmisdi Metodu ilk kesf eden Iohan Bernulli mektubunda Lopitala bu haqda bildirmisdi Menbe Arxivlenmis suret PDF 2009 02 06 tarixinde PDF Istifade tarixi 2013 11 26 Paul J Nahin An Imaginary Tale The Story of 1 displaystyle sqrt 1 p 216 Riyaziyyat ile elaqedar bu meqale qaralama halindadir Meqaleni redakte ederek Vikipediyani zenginlesdirin Etdiyiniz redakteleri menbe ve istinadlarla esaslandirmagi unutmayin
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська