Bu məqaləni lazımdır. |
Ardıcıl yaxınlaşma üsulunda hər bir yaxınlaşmada müəyyən inteqrallar hesablanır. Əksər hallarda müəyyən inteqralları dəqiq üsullarla hesablamaq mümkün olmur və təqribi üsullardan istifadə olunur. Tutaq ki,
diferensial tənliyinin başlanğıc şərtini ödəyən həllini parçasında tapmaq tələb olunur parçasını addımı ilə bərabər hissəyə bölək:
parçasında tənliyini inteqrallayaq.
parçasında funksiyasının qiymətini sabit, nöqtəsindəki qiymətinə bərabər götürsək (1) aşağıdakı kimi yazılar:
(2) nöqtəsində tənliyin həllinə çəkilmiş toxunanın tənliyidir. Sanki parçasında tənliyin həlli abisisi olan nöqtədə çəkilmiş toxunana paralel və nöqtəsindən keçən düz xətt parçası ilə əvəz olunur. Nəticədə həllə yaxın sınıq xətləri alırıq ki, bu sınıq xəttə Eyler sınıq xətti deyilir. olduğunu nəzərə alsaq və sadə işarələmələrdən istifadə etsək, hesabat düsturlarını aşağıdakı şəkildə yaza bilərik:
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Bu meqaleni vikilesdirmek lazimdir Lutfen meqaleni umumvikipediya ve redakte qaydalarina uygun sekilde tertib edin Ardicil yaxinlasma usulunda her bir yaxinlasmada mueyyen inteqrallar hesablanir Ekser hallarda mueyyen inteqrallari deqiq usullarla hesablamaq mumkun olmur ve teqribi usullardan istifade olunur Tutaq ki y x f x y displaystyle y prime x f x y diferensial tenliyinin y x0 y0 displaystyle y x 0 y 0 baslangic sertini odeyen hellini a b displaystyle a b parcasinda tapmaq teleb olunur a b displaystyle a b parcasini h displaystyle h addimi ile n displaystyle n beraber hisseye bolek h b an xi x0 ih i 0 1 2 displaystyle h frac b a n x i x 0 ih i 0 1 2 ldots xk xk 1 displaystyle x k x k 1 parcasinda tenliyini inteqrallayaq xkxk 1y x dx xkxk 1f x y dx displaystyle int limits x k x k 1 y prime x dx int limits x k x k 1 f x y dx y x xkxk 1 xkxk 1f x y dx y xk 1 y xk xkxk 1f x y dx displaystyle y x x k x k 1 int limits x k x k 1 f x y dx Rightarrow y x k 1 y x k int limits x k x k 1 f x y dx 1 xk xk 1 displaystyle x k x k 1 parcasinda f x y displaystyle f x y funksiyasinin qiymetini sabit xk yk displaystyle x k y k noqtesindeki qiymetine beraber gotursek 1 asagidaki kimi yazilar y xk 1 y xk f xk yk xk 1 xk y xk f xk yk h displaystyle y x k 1 y x k f x k y k x k 1 x k y x k f x k y k h 2 2 xk yk displaystyle x k y k noqtesinde tenliyin y x displaystyle y x helline cekilmis toxunanin tenliyidir Sanki xk xk 1 displaystyle x k x k 1 parcasinda tenliyin helli abisisi xk displaystyle x k olan noqtede cekilmis toxunana paralel ve xk yk displaystyle x k y k noqtesinden kecen duz xett parcasi ile evez olunur Neticede helle yaxin siniq xetleri aliriq ki bu siniq xette Eyler siniq xetti deyilir xk 1 xk h displaystyle x k 1 x k h oldugunu nezere alsaq ve sade isarelemelerden istifade etsek hesabat dusturlarini asagidaki sekilde yaza bilerik yk 1 yk f xk yk h displaystyle y k 1 y k f x k y k h
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State
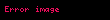

![{\displaystyle [a,b]}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4NVl6UmlOemc0Wm1NMVl6WXpOMlV5Tm1WbE9UaGlORFZtT0RsaE5XTXdPR000TldZM09UTTEuc3Zn.svg)



![{\displaystyle [x_{k},x_{k+1}]}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5aFpUSTROV1ppWTJFMU5tRTJPRFV4TXpWaU16Rmpaams1Tm1Oa1pEVXhPV1k0WlRJeFpUQmwuc3Zn.svg)