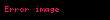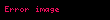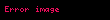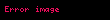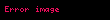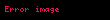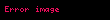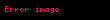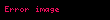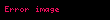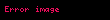İbtidai funksiya (və ya qeyri-müəyyən inteqral; törəmənin əksi) verilmiş aralığın bütün nöqtələrində F(x)=f'(x) bərabərliyini ödəyən funksiya. F(x) funksiyasına həmin aralıqda f(x) funksiyasının ibtidai funksiyası deyilir.
Nümunə: Göstərək ki, funksiyası aralığında funksiyasının ibtidai funksiyasıdır.
Doğrudan da aralığının istənilən nöqtəsində bərabərliyi ödənilir. Tutaq ki funksiyası verilmiş aralıqda kəsilməz funksiyasının ibtidai funksiyasıdır. Onda ixtiyarı sabitı üçün funksiyası da həmin aralıqda funksiyasının ibtidai funksiyasıdır.
Əsas xassələri
Qeyri müəyyən inteqralın (ibtidai funksiya) aşağıdakı xassələri var.
1: Qeyri müəyyən inteqralın törəməsi inteqralaltı funksiya diferensialı isə inteqralaltı ifadəyə bərabərdir:
- İsbatı: Tutaq ki, F(x) funksiya ibtidai f(x)-sin funksiyasıdır: F(x)=f(x). Onda
yaza bilərik. Bu bərabərliyin hər iki tərəfindən törəmə alsaq,
,
yəni
.
2.Kəsilməz törəməsi olan F(x) funksiyasını törəməsinin qeyri-müəyyən inteqralı onun özündən sabit toplananla fərqlənir, yəni
və ya
.
Burada F(x)-kəsilməz diferensiallanan funksiyadır. Bu xassə, bilavasitə qeyri-müəyyən inteqralın tərifindən alınır.
3.Sıfırdan fərqli sabit vuruğu inteqral işarəsi xaricinə çıxarmaq olar.
Doğrudan da, F'(x)=f(x) isə, sıfırdan fərqli k sabiti üçün 
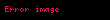
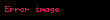
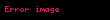
.
4. Cəmin qeyri-müəyyən inteqralı toplananların qeyri -müəyyən ınteqralları cəminə bərabərdir:
Mənbə
- Cəbr və analizin başlanğıcı - Ümumtəhsil məktəblərinin XI sinfi üçün dərslik; M.C.Mərdanov, M.H.Yaqubov, S.S.Mirzəyev, A.B.İbrahimov,K.N.İsmayilzadə, İ.H.Hüseynov, M.A.Kərimov, Ə.F.Quliyev; Çaşıoğlu nəş. 2007.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Ibtidai funksiya ve ya qeyri mueyyen inteqral toremenin eksi verilmis araligin butun noqtelerinde F x f x beraberliyini odeyen funksiya F x funksiyasina hemin araliqda f x funksiyasinin ibtidai funksiyasi deyilir Numune Gosterek ki F x 3x4 displaystyle F x 3x 4 funksiyasi displaystyle infty infty araliginda f x 12x3 displaystyle f x 12x 3 funksiyasinin ibtidai funksiyasidir F x 3x4 3 x4 3 4x3 12x3 f x displaystyle F x 3x 4 3 x 4 3 cdot 4x 3 12x 3 f x Dogrudan da araliginin istenilen noqtesinde beraberliyi odenilir Tutaq ki funksiyasi verilmis araliqda kesilmez funksiyasinin ibtidai funksiyasidir Onda ixtiyari sabiti ucun funksiyasi da hemin araliqda funksiyasinin ibtidai funksiyasidir Esas xasseleriQeyri mueyyen inteqralin ibtidai funksiya asagidaki xasseleri var 1 Qeyri mueyyen inteqralin toremesi inteqralalti funksiya diferensiali ise inteqralalti ifadeye beraberdir f x dx f x displaystyle int f x dx f x d f x dx f x dx displaystyle d int f x dx f x dx Isbati Tutaq ki F x funksiya ibtidai f x sin funksiyasidir F x f x Onda f x dx F x C displaystyle int f x dx F x C yaza bilerik Bu beraberliyin her iki terefinden toreme alsaq f x dx F x C F x C displaystyle int f x dx F x C F x C yeni f x dx f x displaystyle int f x dx f x dd 2 Kesilmez toremesi olan F x funksiyasini toremesinin qeyri mueyyen inteqrali onun ozunden sabit toplananla ferqlenir yeni F x dx F x C displaystyle int F x dx F x C ve ya dF x dx F x C displaystyle int dF x dx F x C Burada F x kesilmez diferensiallanan funksiyadir Bu xasse bilavasite qeyri mueyyen inteqralin terifinden alinir 3 Sifirdan ferqli sabit vurugu inteqral isaresi xaricine cixarmaq olar kf x dx k f x dx k 0 displaystyle int kf x dx k int f x dx k neq 0 Dogrudan da F x f x ise sifirdan ferqli k sabiti ucun kF x kF x kf x displaystyle kF x kF x kf x oldugundan kf x dx kF x C k f x dx displaystyle int kf x dx kF x C k int f x dx aliriq xa 1 a 1 xa displaystyle x alpha 1 alpha 1 x alpha oldugundan 2 ci ve 3 cu xasseleri tetbiq etmekle bele neticeye gelirik ki istenilen a 1 displaystyle alpha neq 1 ucun xadx 1a 1 a 1 xadx 1a 1 xa 1 dx xa 1a 1 C displaystyle int x alpha dx frac 1 alpha 1 int alpha 1 x alpha dx frac 1 alpha 1 int x alpha 1 dx frac x alpha 1 alpha 1 C 4 Cemin qeyri mueyyen inteqrali toplananlarin qeyri mueyyen inteqrallari cemine beraberdir f x g x dx f x dx g x dx displaystyle int f x g x dx int f x dx int g x dx MenbeCebr ve analizin baslangici Umumtehsil mekteblerinin XI sinfi ucun derslik M C Merdanov M H Yaqubov S S Mirzeyev A B Ibrahimov K N Ismayilzade I H Huseynov M A Kerimov E F Quliyev Casioglu nes 2007
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State