Normal paylanma və ya Qauss paylanması – kəsilməz ehtimal paylanmasının vacib növü. Fiziki kəmiyyət bir çox təsadüfi amillərin təsirinə məruz qaldıqda o normal paylanmaya tabe olur. Məlumdur ki, belə hallar təbiətdə çox rast gəlinir. Onlardan normal paylanma geniş yayılmışdır, onun adı da buradan götürülmüşdür.

Normal paylanmanın mahiyyəti əsaslanır. Burada deyilir ki, bir-birindən asılı olmayan, identik paylanmış təsadüfi dəyişənlərin sərhəd qiymətləri normal paylanır. Təsadüfi dəyişənlər o vaxt normal paylanırlar ki, onlar çoxlu sayda amillərin təsirlərinin cəmlənməsindən yaranır və hər bir amil ayrı-ayrılıqda heç bir əhəmiyyətli təsirə malik deyil.
Təsadüfi parametrlərin normal paylanmasından sürətlərin, ölçü xətalarının, nəzarət xətalarının təyini zamanı aparılan sınaqlar zamanı istifadə edilir.
Riyazi və statatistik qiymətləndirmələr zamanı qiymətləndirilən funksiya əmsallarının meyilli olub olmamasının təyin edilməsi üçün normal paylanmadan istifadə edilir.
Təyinatı
Ehtimal paylanma sıxlığı 
o vaxt 


Normal paylanmanın sıxlıq funksiyası
.
ilə təsvir olunur.
Xassələri


Belə dəyişənlərin paylanma funksiyası elementar funksiya ilə təyin olunmur və

kimi Riman inteqralının köməyi ilə təsvir olunur.
Standart normal dəyişən üçün paylanma funksiyası bərabərdir:

Ümumi normal dəyişən üçün normal paylanma 

Standart təsadüfi dəyişənin 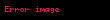

Buradan alınır ki, standart normal dəyişənin 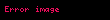

burada 


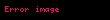
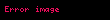

Normal paylanmanın xarakteristik funksiyası belədir:

burada 

İstinadlar
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Normal paylanma ve ya Qauss paylanmasi kesilmez ehtimal paylanmasinin vacib novu Fiziki kemiyyet bir cox tesadufi amillerin tesirine meruz qaldiqda o normal paylanmaya tabe olur Melumdur ki bele hallar tebietde cox rast gelinir Onlardan normal paylanma genis yayilmisdir onun adi da buradan goturulmusdur Normal paylanmanin sixligi Yasil xett standart normal paylanmani gosterir Normal paylanmanin mahiyyeti esaslanir Burada deyilir ki bir birinden asili olmayan identik paylanmis tesadufi deyisenlerin serhed qiymetleri normal paylanir Tesadufi deyisenler o vaxt normal paylanirlar ki onlar coxlu sayda amillerin tesirlerinin cemlenmesinden yaranir ve her bir amil ayri ayriliqda hec bir ehemiyyetli tesire malik deyil Tesadufi parametrlerin normal paylanmasindan suretlerin olcu xetalarinin nezaret xetalarinin teyini zamani aparilan sinaqlar zamani istifade edilir Riyazi ve statatistik qiymetlendirmeler zamani qiymetlendirilen funksiya emsallarinin meyilli olub olmamasinin teyin edilmesi ucun normal paylanmadan istifade edilir TeyinatiEhtimal paylanma sixligi f R R x f x displaystyle f mathbb R to mathbb R x mapsto f x olan bir kesilmez tesadufi deyisen ucun f x 1s2pexp 12 x ms 2 displaystyle f x frac 1 sigma sqrt 2 pi exp left frac 1 2 left frac x mu sigma right 2 right o vaxt m displaystyle mu s displaystyle sigma normal paylanir ki X N m s2 displaystyle X sim mathcal N mu sigma 2 ve ya m s2 displaystyle mu sigma 2 da normal paylansin burada m displaystyle mu riyazi gozlemeni orta kemiyyet ve s displaystyle sigma tesadufi kemiyyetin variyansidir Normal paylanmanin sixliq funksiyasi F x 1s2p xexp 12 t ms 2 dt displaystyle F x frac 1 sigma sqrt 2 pi int infty x exp left frac 1 2 left frac t mu sigma right 2 right mathrm d t ile tesvir olunur Xasselerim displaystyle mu surusme parametri ve s displaystyle sigma dispersiyasina malik tesadufi deyisenli normal paylanmanin ehtimal sixligi bele hesablanir p x 1s2pexp x m 22s2 displaystyle p x frac 1 sigma sqrt 2 pi exp left frac x mu 2 2 sigma 2 right Bele deyisenlerin paylanma funksiyasi elementar funksiya ile teyin olunmur ve F x 1s2p xexp t m 22s2 dt displaystyle F x frac 1 sigma sqrt 2 pi int infty x exp left frac t mu 2 2 sigma 2 right dt kimi Riman inteqralinin komeyi ile tesvir olunur Standart normal deyisen ucun paylanma funksiyasi beraberdir F x 0 1 12p xexp t22 dt displaystyle operatorname F x 0 1 frac 1 sqrt 2 pi int infty x exp left frac t 2 2 right dt Umumi normal deyisen ucun normal paylanma F0 displaystyle F 0 vasitesile bele tesvir olunur F x m s F x ms 0 1 displaystyle operatorname F x mu sigma F left frac x mu sigma 0 1 right Standart tesadufi deyisenin 0 displaystyle 0 nezeren simmetrik sixligi 0exp t m 22s2 dt 0 5 displaystyle int infty 0 exp left frac t mu 2 2 sigma 2 right dt 0 5 Buradan alinir ki standart normal deyisenin 0 x displaystyle 0 x intervalina dusme ehtimali beraberdir F x 0 1 0 5 0xexp t22 dt 0 5 F x displaystyle operatorname F x 0 1 0 5 int 0 x exp left frac t 2 2 right dt 0 5 Phi x burada F x displaystyle Phi x Laplas funsiyasidir F x 12p 0xexp t22 dt displaystyle operatorname Phi x frac 1 sqrt 2 pi int 0 x exp left frac t 2 2 right dt m displaystyle mu ve s displaystyle sigma parametrlerine malik standart normal deyisenin a b displaystyle alpha beta intervalina dusme ehtimali P a lt X lt b F b ms F a ms displaystyle operatorname P alpha lt X lt beta Phi frac beta mu sigma Phi frac alpha mu sigma Normal paylanmanin xarakteristik funksiyasi beledir f t E eit3 exp imt s2t22 displaystyle f t operatorname E e it xi exp left i mu t frac sigma 2 t 2 2 right burada 3 N m s2 displaystyle xi sim N mu sigma 2 tesadufi deyiseninin parametrleri m displaystyle mu ve s displaystyle sigma olan normal paylanmadir Istinadlar
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State

