Səth — həndəsənin əsas anlayışlarından biri. Bu anlayış cismin sərhədi və ya hərəkət edən xəttin izi kimi sadə təsəvvürlərin riyazi mücərrədləşməsidir.
Səthin sadə hissəsi üçölçülü fəzanın elə çoxluğudur ki, o, kvadratı ilə homeomorfdur. və çoxluqları arasında homeomorfluq <center
funksiyaları ilə verilir. Burada kvadratının daxili nöqtələrinin koordinatları, isə -yə uyğun nöqtənin koordinatlarıdır. və ədədlərini çoxluğunda əyrixətli koordinatlar adlandırırlar.
Səthin sadə hissəsi ilə müqayisədə düzgün səth daha ümumi anlayışdır. Düzgün səth fəzanın elə nöqtələri çoxluğudur ki, bu çoxluqda hər bir nöqtənin kiçik ətrafı səthin sadə hissəsi olsun. Bu tərif üçölçülü fəzada ikiölçülü həndəsi obrazların tərifi ilə eynidir. Bu tərifi də, məsələn, kənarı olan səth ödəmir.
Çox məsələlərdə tənliyinin həlləri olan üçölçülü fəzanın nöqtələri çoxluğunu səth adlandırırlar. Bu cür təyin edilən səth bizim səth haqqında təsəvvurlərimizə uyğun gəlmir.
Məsələn, verilmiş tənliyin həlləri çoxluğu boş çoxluq ola bilər. Səth anlayışı bütövlükdə səthlər nəzəriyyəsində öyrənilir.
Müxtəlif fiqurlar üçün səth düsturları
| Fiqura | Səthin sahəsi S üçün düstur | İzahat |
|---|---|---|
| Kvadrat | 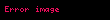 |  = Tərəfin uzunluğu = Tərəfin uzunluğu |
| Düzbucaqlı | 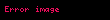 | 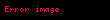 = Tərəfin uzunluğu = Tərəfin uzunluğu |
| Üçbucaq | 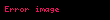 | 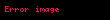 = Oturacaq xəttinin uzunluğu, = Oturacaq xəttinin uzunluğu, 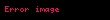 = Oturacaq xəttə perpendikulyar olan hündürlük = Oturacaq xəttə perpendikulyar olan hündürlük |
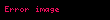 |  = Tərəfin uzunluğu = Tərəfin uzunluğu | |
| Trapesiya | 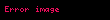 | 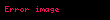 = Tərəfin uzunluğu, = Tərəfin uzunluğu, 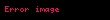 = Yan xəttə perpendikulyar olan hündürlük = Yan xəttə perpendikulyar olan hündürlük |
| Romb | 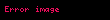 | 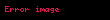 = Diagonallar = Diagonallar |
| Paraleloqram | 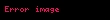 |  = Tərəfin uzunluğu, = Tərəfin uzunluğu,  = Yan xəttə perpendikulyar olan hündürlük = Yan xəttə perpendikulyar olan hündürlük  |
| Kürə səthinin sahəsi | 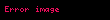 | 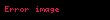 = Radius = Radius |
| Çevrə | 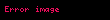 | 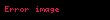 = Radius = Radius |
 |  = Tərəfin uzunluğu = Tərəfin uzunluğu |
Ədəbiyyat
- M. Mərdanov, S. Mirzəyev, Ş. Sadıqov Məktəblinin riyaziyyatdan izahlı lüğəti. Bakı 2016, "Radius nəşriyyatı", 296 səh.
- Azərbaycan Sovet Ensklopediyası. I–X cild, Bakı 1976–1987.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Seth hendesenin esas anlayislarindan biri Bu anlayis cismin serhedi ve ya hereket eden xettin izi kimi sade tesevvurlerin riyazi mucerredlesmesidir Sethin sade hissesi ucolculu fezanin ele D displaystyle D coxlugudur ki o E2 displaystyle E 2 kvadrati ile homeomorfdur D displaystyle D ve E2 displaystyle E 2 coxluqlari arasinda homeomorfluq lt center x x u v y y u v z z u v displaystyle x x u v y y u v z z u v funksiyalari ile verilir Burada u v displaystyle u v E2 displaystyle E 2 kvadratinin daxili noqtelerinin koordinatlari x y z displaystyle x y z ise u v displaystyle u v ye uygun noqtenin koordinatlaridir u displaystyle u ve v displaystyle v ededlerini D displaystyle D coxlugunda eyrixetli koordinatlar adlandirirlar Sethin sade hissesi ile muqayisede duzgun seth daha umumi anlayisdir Duzgun seth fezanin ele noqteleri coxlugudur ki bu coxluqda her bir noqtenin kicik etrafi sethin sade hissesi olsun Bu terif ucolculu fezada ikiolculu hendesi obrazlarin terifi ile eynidir Bu terifi de meselen kenari olan seth odemir Cox meselelerde ϕ x y z 0 displaystyle phi x y z 0 tenliyinin helleri olan ucolculu fezanin noqteleri coxlugunu seth adlandirirlar Bu cur teyin edilen seth bizim seth haqqinda tesevvurlerimize uygun gelmir Meselen verilmis tenliyin helleri coxlugu bos coxluq ola biler Seth anlayisi butovlukde sethler nezeriyyesinde oyrenilir Muxtelif fiqurlar ucun seth dusturlariFiqura Sethin sahesi S ucun dustur IzahatKvadrat S a a S a2 displaystyle S a cdot a quad S a 2 a displaystyle a Terefin uzunluguDuzbucaqli S a b displaystyle S a cdot b a b displaystyle a b Terefin uzunluguUcbucaq S g h2 displaystyle S frac g cdot h 2 g displaystyle g Oturacaq xettinin uzunlugu h displaystyle h Oturacaq xette perpendikulyar olan hundurlukBeraberterefli ucbucaq S 34a2 displaystyle S frac sqrt 3 4 a 2 a displaystyle a Terefin uzunluguTrapesiya S a c2 h displaystyle S frac a c 2 cdot h a c displaystyle a c Terefin uzunlugu h displaystyle h Yan xette perpendikulyar olan hundurlukRomb S AC BD 2 displaystyle S frac overline AC cdot overline BD 2 AC BD displaystyle overline AC overline BD DiagonallarParaleloqram S a ha displaystyle S a cdot h a a displaystyle a Terefin uzunlugu ha displaystyle h a Yan xette perpendikulyar olan hundurluk a displaystyle a Kure sethinin sahesi S 4p r2 displaystyle S 4 pi cdot r 2 r displaystyle r RadiusCevre S r r p S r2 p displaystyle S r cdot r cdot pi quad S r 2 cdot pi r displaystyle r RadiusS 32a23 displaystyle S frac 3 2 a 2 sqrt 3 a displaystyle a Terefin uzunluguEdebiyyatM Merdanov S Mirzeyev S Sadiqov Mekteblinin riyaziyyatdan izahli lugeti Baki 2016 Radius nesriyyati 296 seh Azerbaycan Sovet Ensklopediyasi I X cild Baki 1976 1987
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State