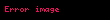Tənbölən (lat. bi- "ikiqat" və sectio "bölmə") və ya "bucağın tənböləni" — başlanğıcı bucağın təpəsində olan və onu iki bərabər bucağa ayıran parçaya deyilir. Tənböləni bucağın daxilində yerləşən və onun tərəflərindən eyni uzaqlıqda olan nöqtələrin həndəsi yeri kimi də təyin etmək olar.

Üçbucağın təpəsini onun qarşı tərəfi ilə birləşdirən və bu təpədəkı bucağı yarıya bölən parçaya üçbucağın tənböləni deyilir.
Üçbucağın üç tənböləni var.
Bərabəryanlı üçbucağın xassələri
- Üçbucağın iki tənböləni bərabərdirsə, onda üçbucaq bərabəryanlıdır və digər tənböləni həm üçbucağın medianı, həm də hündürlüyüdür. Bunun tərsi də doğrudur: bərabəryanlı üçbucağın iki tənböləni bərabər, üçüncü tənböləni isə həm medianı, həm də hündürlüyüdür.
- Bərabərtərfli üçbucağın hər üç tənböləni bərabərdir.
- Bərabərtərəfli üçbucağın hər üç xarici bucağının tənböləni qarşı tərəfə paraleldir.
Üçbucağın tənböləni

.
, burada
- yarımperimetrdir.
Uzunluğu uyğun olaraq 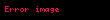
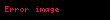
,
,
- Üçbucağın daxili tənbölənlərin kəsişmə nöqtəsi
bucağının tənbölənini
nisbətdə bolür, burada
,
,
— üçbucağın tərəflridir,
— uyğun olaraq
təpəsinin qarşısındakı tərəf,
— uyğun olaraq
təpəsindəki bucaq,
—
tərəfinə çəkilmiş hündürlük.
—
tərəfinə çəkilmiş daxili tənbölən,
—
daxili tənböləninin
tərəfini böldüyü parçaların uzunluqları,
—
təpəsindən
tərəfinin uzantısına çəkilmiş xarici tənböləninin uzunluğu.
—
xarici tənböləninin
tərəfinin uzantısı ilə kəsişmə nöqtəsini də özündə saxlayan parçanin bölündüyü hissələrin uzunluqlarıdır.
Xarici keçidlər
[1]
- Simons, Stuart. Mathematical Gazette 93, March 2009, 115-116.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Tenbolen lat bi ikiqat ve sectio bolme ve ya bucagin tenboleni baslangici bucagin tepesinde olan ve onu iki beraber bucaga ayiran parcaya deyilir Tenboleni bucagin daxilinde yerlesen ve onun tereflerinden eyni uzaqliqda olan noqtelerin hendesi yeri kimi de teyin etmek olar AD tenboleni A bucagini yariya bolur Ucbucagin tepesini onun qarsi terefi ile birlesdiren ve bu tepedeki bucagi yariya bolen parcaya ucbucagin tenboleni deyilir Ucbucagin uc tenboleni var Beraberyanli ucbucagin xasseleri Ucbucagin iki tenboleni beraberdirse onda ucbucaq beraberyanlidir ve diger tenboleni hem ucbucagin mediani hem de hundurluyudur Bunun tersi de dogrudur beraberyanli ucbucagin iki tenboleni beraber ucuncu tenboleni ise hem mediani hem de hundurluyudur Beraberterfli ucbucagin her uc tenboleni beraberdir Beraberterefli ucbucagin her uc xarici bucaginin tenboleni qarsi terefe paraleldir Ucbucagin tenboleniABC ucbucaginin tenboleni lc ab a b c a b c a b 2abp p c a b displaystyle l c sqrt ab a b c a b c over a b frac 2 sqrt abp p c a b burada p displaystyle p yarimperimetrdir lc ab albl displaystyle l c sqrt ab a l b l lc 2abcos g2a b displaystyle l c frac 2ab cos frac gamma 2 a b lc hccos a b2 displaystyle l c frac h c cos frac alpha beta 2 Uzunlugu uygun olaraq la lb displaystyle l a l b ve lc displaystyle l c olan A B ve C bucaqlarinin tenbolenleri ucun agagidaki dogrudur b c 2bcla2 c a 2calb2 a b 2ablc2 a b c 2 displaystyle frac b c 2 bc l a 2 frac c a 2 ca l b 2 frac a b 2 ab l c 2 a b c 2 wc2 aw bw ab CE2 BE AE ab displaystyle w c 2 a w cdot b w ab CE 2 BE cdot AE ab Ucbucagin daxili tenbolenlerin kesisme noqtesi A displaystyle A bucaginin tenbolenini b ca displaystyle frac b c a nisbetde bolur burada a displaystyle a b displaystyle b c displaystyle c ucbucagin tereflridir a b c displaystyle a b c uygun olaraq A B C displaystyle A B C tepesinin qarsisindaki teref a b g displaystyle alpha beta gamma uygun olaraq A B C displaystyle A B C tepesindeki bucaq hc displaystyle h c c displaystyle c terefine cekilmis hundurluk lc displaystyle l c c displaystyle c terefine cekilmis daxili tenbolen al bl displaystyle a l b l lc displaystyle l c daxili tenboleninin c displaystyle c terefini bolduyu parcalarin uzunluqlari wc displaystyle w c C displaystyle C tepesinden AB displaystyle AB terefinin uzantisina cekilmis xarici tenboleninin uzunlugu aw bw displaystyle a w b w wc displaystyle w c xarici tenboleninin c AB displaystyle c AB terefinin uzantisi ile kesisme noqtesini de ozunde saxlayan parcanin bolunduyu hisselerin uzunluqlaridir Xarici kecidler 1 Simons Stuart Mathematical Gazette 93 March 2009 115 116
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State