Bu məqaləni lazımdır. |
Teorem
Tutaq ki, 


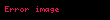
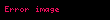
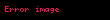
şərtini ödəyən həqiqi xətti funksionaldır. Onda 

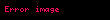
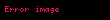
şərtini ödəyən 
İsbatı






Ədəbiyyat
1. Ə.H.Əhmədov. Xətti analizin üç prinsipi. Dərs vəsaiti. Bakı: «Bakı Universiteti» nəşriyyatı, 2008, 112 s.
2. Elşar Qurban oğlu Orucov. Tətbiqi funksional analizin elementləri: Bakı “BDU nəşriyyatı”, 2008, 234 səh. 2017-05-17 at the Wayback Machine
3. А.Н.Колмогоров, С.М.Фомин. Элементы теории функции и функционального анализа. М., 1988 г
4. Л.А.Люстерник, В.И.Соболев. Элементы функционального анализа. М., 1965г.
5.Л.В.Канторович, Г.П.Акилов. Функциональный анализ в нормированных пространствах.М., 1959 г.
6.М.Рид, Б.Саймон. Методы современной математической физики, т.1.Функциональный анализ, 1977 г.
7.В.А.Треногин. Задачи и упражнения по функциональному анализу.М., 1984 г.
8.Ə.Həbibzadə. Funksional analiz. Bakı, 1988
Həmçinin bax
Математический анализ, функциональный анализ
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Bu meqaleni vikilesdirmek lazimdir Lutfen meqaleni umumvikipediya ve redakte qaydalarina uygun sekilde tertib edin TeoremTutaq ki p displaystyle p funksionali E displaystyle E heqiqi xetti fezasinda teyin olunmus bircins qabariq funksional f displaystyle f ise mueyyen L E displaystyle L subset E xetti altfezasinda teyin olunmus ve istenilen x L displaystyle x in L unsuru ucun f x p x displaystyle f x leq p x sertini odeyen heqiqi xetti funksionaldir Onda f displaystyle f funksionalini butun E displaystyle E fezasinda teyin olunan ve istenilen x E displaystyle x in E unsuru ucun F x p x displaystyle F x leq p x sertini odeyen F displaystyle F heqiqi xetti funksionalina davam etdirmek olar Isbatif displaystyle f funksionalinin her bir x D f displaystyle x in D f prime unsuru ucun f x p x displaystyle f prime x leq p x berabersizliyini odeyen butun f displaystyle f prime xetti davamlari coxlugunu Fp displaystyle F p ile isare edek Burada D f displaystyle D f prime f displaystyle f prime funksionalinin teyin oblastidir f1 f2 Fp displaystyle f 1 prime f 2 prime in F p funksionallarindan f2 displaystyle f 2 prime funksionali f1 displaystyle f 1 prime in davami olduqda bunu f1 lt f2 displaystyle f 1 prime lt f 2 prime seklinde ifade edek Onda Fp displaystyle F p bu munasibete nezeren qismen nizamlanmis coxluq olar Eger Fp displaystyle F p prime le Fp displaystyle F p nin xetti nizamlanmis hissesini isare etsek f FpD f displaystyle bigcup limits f prime in F p D f prime coxlugunda teyin olunan ve her bir x D f displaystyle x in D f prime f Fp displaystyle f prime in F p prime ucun f0 x f x displaystyle f 0 x f prime x kimi verilen f0 displaystyle f 0 funksionali Fp displaystyle F p prime coxlugunun yuxari serheddi olacaqdir Bu da onu gosterir ki Fp displaystyle F p coxlugu Sorn lemmasinin sertlerini odeyir Onda bu lemmaya gore Fp displaystyle F p coxlugu F displaystyle F maksimal unsurune malikdir Asanliqla gormek olar ki f displaystyle f maksimal funksionalinin teyin oblasti butun E displaystyle E oblasti ile ust uste dusur Eks halda f displaystyle f funksionalinin D F displaystyle D F teyin oblastindan munasibetini odemekle davam etdirmek olardi Bu ise F displaystyle F in maksimal unsur olmasina zidd olardi Bununla teorem isbat olundu Edebiyyat1 E H Ehmedov Xetti analizin uc prinsipi Ders vesaiti Baki Baki Universiteti nesriyyati 2008 112 s 2 Elsar Qurban oglu Orucov Tetbiqi funksional analizin elementleri Baki BDU nesriyyati 2008 234 seh 2017 05 17 at the Wayback Machine 3 A N Kolmogorov S M Fomin Elementy teorii funkcii i funkcionalnogo analiza M 1988 g 4 L A Lyusternik V I Sobolev Elementy funkcionalnogo analiza M 1965g 5 L V Kantorovich G P Akilov Funkcionalnyj analiz v normirovannyh prostranstvah M 1959 g 6 M Rid B Sajmon Metody sovremennoj matematicheskoj fiziki t 1 Funkcionalnyj analiz 1977 g 7 V A Trenogin Zadachi i uprazhneniya po funkcionalnomu analizu M 1984 g 8 E Hebibzade Funksional analiz Baki 1988Hemcinin baxMatematicheskij analiz funkcionalnyj analiz
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State