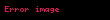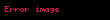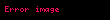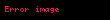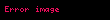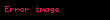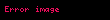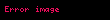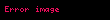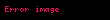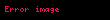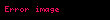Uzunluq riyaziyyatda parça, yol və əyrilərin xassələrini səciyyələndirir. Əyrinin uzunluğu həmçinin "qövs uzunluğu" da adlanır.
Parçanın uzunluğu
Əgər, uyğun olaraq 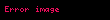
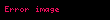



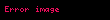
Müstəvidə yolun uzunluğu
Müstəvi üzərində və ya fəzada yol iki və ya üç koordinat funksiyası ilə verilir:
uyğun olaraq
,
şərti daxilində.
Hissə-hissə kəsilməyən yolun uzunluğu onun vektorunun inteqrallanması ilə əldə edilir:
uyğun olaraq
Polyar koordinat sistemində yolun uzunluğu
Müstəvidə verilmiş yol polyar koordinat sistemnində 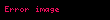
üçün
hasil qaydasından alınır
və
, bununla
.
Buradan polyar koordinat siistemondə yolun uzunluğu belə tapılır:
.
Həmçinin bax
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Bu adin diger istifade formalari ucun bax Uzunluq deqiqlesdirme Uzunluq riyaziyyatda parca yol ve eyrilerin xasselerini seciyyelendirir Eyrinin uzunlugu hemcinin qovs uzunlugu da adlanir Parcanin uzunluguEger uygun olaraq a1 a2 a3 displaystyle a 1 a 2 a 3 b1 b2 b3 displaystyle b 1 b 2 b 3 koordinatlarina malik A displaystyle A ve B displaystyle B noqteleri verilmis R3 displaystyle mathbb R 3 aiddrse onda bu koordinatlar arasindaki AB displaystyle AB parcasinin uzunlugu Pifaqor teoremine gore hesablanir AB a1 b1 2 a2 b2 2 a3 b3 2 displaystyle AB sqrt a 1 b 1 2 a 2 b 2 2 a 3 b 3 2 Mustevide yolun uzunluguMustevi uzerinde ve ya fezada yol iki ve ya uc koordinat funksiyasi ile verilir t x t y t displaystyle t mapsto x t y t uygun olaraq t x t y t z t displaystyle t mapsto x t y t z t a t b displaystyle a leq t leq b serti daxilinde Hisse hisse kesilmeyen yolun uzunlugu onun vektorunun inteqrallanmasi ile elde edilir L abx t 2 y t 2dt displaystyle L int a b sqrt dot x t 2 dot y t 2 mathrm d t uygun olaraq abx t 2 y t 2 z t 2dt displaystyle int a b sqrt dot x t 2 dot y t 2 dot z t 2 mathrm d t Polyar koordinat sisteminde yolun uzunluguMustevide verilmis yol polyar koordinat sistemninde r f displaystyle r varphi seklind teyin olunmussa onda f0 f f1 displaystyle varphi 0 leq varphi leq varphi 1 ucun f r f cos f r f sin f displaystyle varphi mapsto r varphi cos varphi r varphi sin varphi hasil qaydasindan alinir dxdf r f cos f r f sin f displaystyle frac mathrm d x mathrm d varphi r prime varphi cos varphi r varphi sin varphi ve dydf r f sin f r f cos f displaystyle frac mathrm d y mathrm d varphi r prime varphi sin varphi r varphi cos varphi bununla dxdf 2 dydf 2 r f 2 r2 f displaystyle left frac mathrm d x mathrm d varphi right 2 left frac mathrm d y mathrm d varphi right 2 left r prime varphi right 2 r 2 varphi Buradan polyar koordinat siistemonde yolun uzunlugu bele tapilir L f0f1 r f 2 r2 f df displaystyle L int varphi 0 varphi 1 sqrt left r prime varphi right 2 r 2 varphi mathrm d varphi Hemcinin baxUzunluq Fizika Uzunluq Cebr
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська