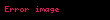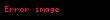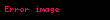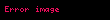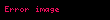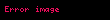Skalyar hasil (bəzən daxili hasil adlanır) — nəticəsi skalar olan, yəni koordinat sisteminin seçimindən asılı olmayan bir rəqəm olan iki vektor üzərində əməliyyat.
İki və vektorunun skalyar hasili-ya deyilir. Burada və və vektorlarının uzunluqları, -bu vektorlar arasındakı bucaqdır. Skalyar hasil "" yaxud "" kimi işarə olunur.Əgər və vektorları düzbucaqlı Dekart koordinat sistemində koordinatlarına malikdirsə, onda skalyar hasil belə ifadə olunur:
Analoji düstur üç və daha çox ölçüsü olan fəza üçün də doğrudur. Skalyar hasil aşağıdakı xassələri var:
yaxud
Kompleks ədədin həndəsi tərifi vektor olduğu üçün bəzən iki kompleks ədədin skalyar hasilinə baxılır. , kompleks ədədlərinin skalyar hasili
cəminə deyilir. İki vektorun skalyar hasilinin bütün xassələri iki kompleks ədədin skalyar hasili üçün də saxlanır.
Ədəbiyyat
M.Mərdanov, S.Mirzəyev, Ş. Sadıqov Məktəblinin riyaziyyatdan izahlı lüğəti. Bakı 2016, "Radius nəşriyyatı", 296 səh.
Azərbaycan Sovet Ensklopediyası. I-X cild, Bakı 1976-1987.
Avqust 05, 2021
skalyar, hasil, bəzən, daxili, hasil, adlanır, nəticəsi, skalar, olan, yəni, koordinat, sisteminin, seçimindən, asılı, olmayan, rəqəm, olan, vektor, üzərində, əməliyyat, displaystyle, displaystyle, displaystyle, vektorunun, skalyar, hasili, displaystyle, cdot,. Skalyar hasil bezen daxili hasil adlanir neticesi skalar olan yeni koordinat sisteminin seciminden asili olmayan bir reqem olan iki vektor uzerinde emeliyyat 1 0 displaystyle 1 0 Iki a displaystyle bar a ve b displaystyle bar b vektorunun skalyar hasili a b cos a displaystyle mid bar a mid cdot mid bar b mid cos alpha ya deyilir Burada a displaystyle mid bar a mid ve a displaystyle mid bar a mid a displaystyle bar a ve b displaystyle bar b vektorlarinin uzunluqlari a displaystyle alpha bu vektorlar arasindaki bucaqdir Skalyar hasil a b displaystyle bar a cdot bar b yaxud a b displaystyle bar a cdot bar b kimi isare olunur Eger a displaystyle bar a ve b displaystyle bar b vektorlari duzbucaqli Dekart koordinat sisteminde a x 1 y 1 b x 2 y 2 displaystyle bar a x 1 y 1 bar b x 2 y 2 koordinatlarina malikdirse onda skalyar hasil bele ifade olunur a b x 1 x 2 y 1 y 2 displaystyle bar a cdot bar b x 1 cdot x 2 y 1 cdot y 2 Analoji dustur uc ve daha cox olcusu olan feza ucun de dogrudur Skalyar hasil asagidaki xasseleri var 1 a b b a displaystyle 1 bar a cdot bar b bar b cdot bar a 2 a a b a a b displaystyle 2 alpha bar a cdot bar b alpha bar a cdot bar b 3 a b c a b a c displaystyle 3 bar a bar b bar c bar a cdot bar b bar a cdot bar c a b 0 a 0 b 0 displaystyle bar a cdot bar b 0 Leftrightarrow bar a bar 0 bar b bar 0 yaxud a b displaystyle bar a perp bar b 2 0 displaystyle 2 0 Kompleks ededin hendesi terifi vektor oldugu ucun bezen iki kompleks ededin skalyar hasiline baxilir z 1 a b i displaystyle z 1 a bi z 2 c d i displaystyle z 2 c di kompleks ededlerinin skalyar hasili z 1 z 2 a c b d displaystyle z 1 cdot z 2 ac bd cemine deyilir Iki vektorun skalyar hasilinin butun xasseleri iki kompleks ededin skalyar hasili ucun de saxlanir Edebiyyat RedakteM Merdanov S Mirzeyev S Sadiqov Mekteblinin riyaziyyatdan izahli lugeti Baki 2016 Radius nesriyyati 296 seh Azerbaycan Sovet Ensklopediyasi I X cild Baki 1976 1987 Menbe https az wikipedia org w index php title Skalyar hasil amp oldid 5486955, wikipedia, oxu, kitab, kitabxana, axtar, tap, hersey,
ne axtarsan burda
, en yaxsi meqale sayti, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, seks, porno, indir, yukle, sex, azeri sex, azeri, seks yukle, sex yukle, izle, seks izle, porno izle, mobil seks, telefon ucun, chat, azeri chat, tanisliq, tanishliq, azeri tanishliq, sayt, medeni, medeni saytlar, chatlar, mekan, tanisliq mekani, mekanlari, yüklə, pulsuz, pulsuz yüklə, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar.
