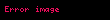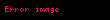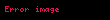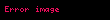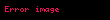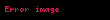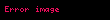sırasına nöqtəsində qüvvət sırası deyilir. Burada əmsalları ədədlərdir. Xüsusi halda olarsa, onda Bu sıraya sıfır nöqtəsində qüvvət sırası deyilir.
Toplama və Çıxma
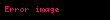

onda
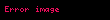
Hasil və Bölmə
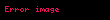
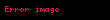
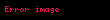
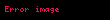
Differensiallama və İnteqrallama
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
n 0 an x c n a0 a1 x c a2 x c 2 an x c n displaystyle sum n 0 infty a n x c n a 0 a 1 x c a 2 x c 2 a n x c n sirasina c displaystyle c noqtesinde quvvet sirasi deyilir Burada an displaystyle a n emsallari ededlerdir Xususi halda c 0 displaystyle c 0 olarsa onda n 0 anxn a0 a1x a2x2 displaystyle sum n 0 infty a n x n a 0 a 1 x a 2 x 2 cdots Bu siraya sifir noqtesinde quvvet sirasi deyilir ex n 0 xnn 1 x x22 x33 displaystyle e x sum n 0 infty frac x n n 1 x frac x 2 2 frac x 3 3 cdots sin x n 0 1 nx2n 1 2n 1 x x33 x55 x77 displaystyle sin x sum n 0 infty frac 1 n x 2n 1 2n 1 x frac x 3 3 frac x 5 5 frac x 7 7 cdots Toplama ve Cixmaf x n 0 an x c n displaystyle f x sum n 0 infty a n x c n g x n 0 bn x c n displaystyle g x sum n 0 infty b n x c n onda f x g x n 0 an bn x c n displaystyle f x pm g x sum n 0 infty a n pm b n x c n Hasil ve Bolmef x g x n 0 an x c n n 0 bn x c n displaystyle f x g x left sum n 0 infty a n x c n right left sum n 0 infty b n x c n right i 0 j 0 aibj x c i j displaystyle sum i 0 infty sum j 0 infty a i b j x c i j n 0 i 0naibn i x c n displaystyle sum n 0 infty left sum i 0 n a i b n i right x c n f x g x n 0 an x c n n 0 bn x c n n 0 dn x c n displaystyle f x over g x sum n 0 infty a n x c n over sum n 0 infty b n x c n sum n 0 infty d n x c n Differensiallama ve Inteqrallamaf x n 1 ann x c n 1 n 0 an 1 n 1 x c n displaystyle f prime x sum n 1 infty a n n left x c right n 1 sum n 0 infty a n 1 left n 1 right left x c right n f x dx n 0 an x c n 1n 1 k n 1 an 1 x c nn k displaystyle int f x dx sum n 0 infty frac a n left x c right n 1 n 1 k sum n 1 infty frac a n 1 left x c right n n k
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State