Azərbaycanca
සිංහල
Türkçe
Permutasiya — təkrarsız yerdəyişmələr.
Tutaq ki, elementlərin sayı m olan çoxluğu verilmişdir. Onun elementlərindən uzunluğu m-ə bərabər olan təkrarsız yerləşdirmələr düzəldək. Deməli, belə yerləşdirmədə M çoxluğunun hər bir elementi bir dəfə iştirak edir. Məsən, m=4 olarsa, belə yerləşdirmələr ... bu qaydada yerləşdirməyi davam etsək onların sayı olar
Tərif
m elementdən uzunluğu m-ə bərabər olan təkrarsız yerləşdirmələr yerdəyişmə adlanır. Tərifə görə belə yerdəyişmələrin sayı 
olar. O, 
ilə işarə edilir. Deməli, 
Adətən "yerdəyişmə" sözü əvəzinə permutasiya sözü işlədilir. Bu düstura görə çıxarış: 
Yəni 
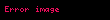
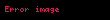
Qeyd
m elementi olan çoxluğun elementlərindən təşkil edilən m elementli təkrarsız yerdəyişmələrin sayı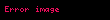 
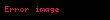
bərabərdir. Buradan alınır ki, bir elementi olan çoxluqdan təşkil edilən yerdəyişmələrin sayı 
olar. Digər tərəfdən, m faktorialın tərifinə görə 
olduğundan, 
Buradan görünür ki, 
olması üçün 
qəbul etmək lazımdır və belə qəbul edilib.
Məsələ
Futbol birinciliyində 8 komanda iştirak edib və komandaların hamısı müxtəlif miqdarda xallar toplayıb. Turnir cədvəlində onlar neçə üsulla yerləşə bilər?
- Həlli: Komandalarının hamısı müxtəlif xallar topladığından, onların cədvəldə yerləşə biləcəyi variantları sayı
![image]()
-ə bərabərdir. Deməli variantları sayı ![image]()
Xarici keçidlər
- Abituriyent jurnalının xüsusi buraxılışı. Redaksiya şurasi: M.M.Abbaszadə, N.Ə.Bayramov, V.M.Bağırov, M.C.Mərdənov və b. Bakı 2005
Həmçinin bax
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Permutasiya tekrarsiz yerdeyismeler 3 topun 6 cur muxtelif permutasiyalari Tutaq ki elementlerin sayi m olan M a1 a2 am displaystyle M a 1 a 2 a m coxlugu verilmisdir Onun elementlerinden uzunlugu m e beraber olan tekrarsiz yerlesdirmeler duzeldek Demeli bele yerlesdirmede M coxlugunun her bir elementi bir defe istirak edir Mesen m 4 olarsa bele yerlesdirmeler a1a2a3a4 a1a2a4a3 a1a4a2a3a4a1a2a3 displaystyle a 1 a 2 a 3 a 4 a 1 a 2 a 4 a 3 a 1 a 4 a 2 a 3 a 4 a 1 a 2 a 3 a2a1a3a4 a2a1a4a3 a2a4a1a3 a4a2a1a3 displaystyle a 2 a 1 a 3 a 4 a 2 a 1 a 4 a 3 a 2 a 4 a 1 a 3 a 4 a 2 a 1 a 3 bu qaydada yerlesdirmeyi davam etsek onlarin sayi 4 24 displaystyle 4 24 olarTerifm elementden uzunlugu m e beraber olan tekrarsiz yerlesdirmeler yerdeyisme adlanir Terife gore bele yerdeyismelerin sayi Amm displaystyle A m m olar O Pm displaystyle P m ile isare edilir Demeli Pm Amm displaystyle P m A m m Adeten yerdeyisme sozu evezine permutasiya sozu isledilir Bu dustura gore cixaris Pm Amm m m 1 m 2 m m 1 m m 1 m 2 2 1 m displaystyle P m A m m m m 1 m 2 cdot m m 1 m m 1 m 2 cdot 2 cdot 1 m Yeni Pm m displaystyle P m m Qeydm elementi olan coxlugun elementlerinden teskil edilen m elementli tekrarsiz yerdeyismelerin sayi Pm 1 2 m 1 m m displaystyle P m 1 cdot 2 cdot m 1 m m beraberdir Buradan alinir ki bir elementi olan coxluqdan teskil edilen yerdeyismelerin sayi Pm 1 1 displaystyle P m 1 1 olar Diger terefden m faktorialin terifine gore m m 1 m displaystyle m m 1 m oldugundan 1 0 1 displaystyle 1 0 cdot 1 Buradan gorunur ki 1 1 displaystyle 1 1 olmasi ucun 0 1 displaystyle 0 1 qebul etmek lazimdir ve bele qebul edilib MeseleFutbol birinciliyinde 8 komanda istirak edib ve komandalarin hamisi muxtelif miqdarda xallar toplayib Turnir cedvelinde onlar nece usulla yerlese biler Helli Komandalarinin hamisi muxtelif xallar topladigindan onlarin cedvelde yerlese bileceyi variantlari sayi P8 displaystyle P 8 e beraberdir Demeli variantlari sayi P8 8 40320 displaystyle P 8 8 40320 Xarici kecidlerAbituriyent jurnalinin xususi buraxilisi Redaksiya surasi M M Abbaszade N E Bayramov V M Bagirov M C Merdenov ve b Baki 2005Hemcinin baxKombinazon Aranjeman Faktorial Binom Coxluq