1.Ayrılış teoremi
Əgər (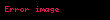
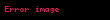
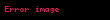
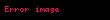

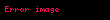
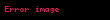


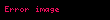
burada
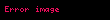
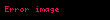
və
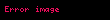
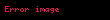
Xüsusi halda:
a)əgər 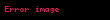
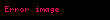
olar, burada
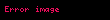
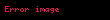
b)əgər 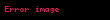
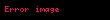
olar, burada
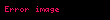
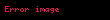
(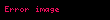
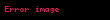
2.Tamlıq şərti
(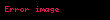
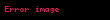
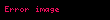
3.Furye sıralarının inteqrallanması
(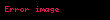
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
1 Ayrilis teoremiEger l l displaystyle l l intervalinda teyin olunmus f x displaystyle f x funksiyasi hisse hisse kesilmezdirse f x displaystyle f x in hisse hisse kesilmez f x displaystyle f x toremesi varsa ve butun 3 displaystyle xi kesilme noqteleri requlyardirsa yeni f 3 12 f 3 0 f 3 0 displaystyle f xi tfrac 1 2 f xi 0 f xi 0 onda bu intervalda f x displaystyle f x funksiyasi Furye sirasi seklinde gosterile biler f displaystyle f x displaystyle x displaystyle a02 n 1 ancos npxl bnsin npxl displaystyle tfrac a 0 2 sum n 1 infty a n cos tfrac n pi x l b n sin tfrac n pi x l 1 burada an 1l llf x cos npxldx displaystyle a n tfrac 1 l int limits l l f x cos tfrac n pi x l dx n displaystyle n 0 1 2 displaystyle 0 1 2 2 ve bn 1l llf x sin npxldx displaystyle b n tfrac 1 l int limits l l f x sin tfrac n pi x l dx n 0 1 2 displaystyle n 0 1 2 2 Xususi halda a eger f x displaystyle f x funksiyasi cutdurse onda f x a02 n 1 ancos npxl displaystyle f x tfrac a 0 2 sum n 1 infty a n cos tfrac n pi x l 3 olar burada an 2l 0lf x cos npxl displaystyle a n tfrac 2 l int limits 0 l f x cos tfrac n pi x l n 0 1 2 displaystyle n 0 1 2 b eger f x displaystyle f x funksiyasi tekdirse onda f x n 1 bnsin npxl displaystyle f x sum n 1 infty b n sin tfrac n pi x l 4 olar burada bn 2l 0lf x sin npxl displaystyle b n tfrac 2 l int limits 0 l f x sin tfrac n pi x l n 0 1 2 displaystyle n 0 1 2 0 l displaystyle 0 l intervalinda teyin olunan ve yuxarida gosterilen kesilmezlik xasselerini odeyen f x displaystyle f x funksiyasini bu intervalda hem 3 dusturu hem de 4 dusturu seklinde gostermek olar 2 Tamliq serti l l displaystyle l l intervalinda kvadrati ile birlikde inteqrallanan ixtiyari f x displaystyle f x funksiyasi ucun 2 ve 2 emsallari vasitesile formal qurulan 1 sirasi Lyapunov beraberliyini odeyir a022 n 1 an2 bn2 1l llf x 2dx displaystyle tfrac a 0 2 2 sum n 1 infty a n 2 b n 2 tfrac 1 l int limits l l f x 2 dx 3 Furye siralarinin inteqrallanmasi l l displaystyle l l intervalinda Riman menada inteqrallanan f x displaystyle f x funksiyasinin hetta dagilan 1 Furye sirasini bu intervalda hedbehed inteqrallamaq olar
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська