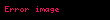Eynşteyn cəmləmə qaydası Albert Eynşteyn tərəfindən, Ümumi Nisbilik Nəzəriyyəsi yazılarkən daha qısa və anlaşıqlı dildə cəmləmə əməliyyatını() ifadə etmək məqsədilə gətirilib. Sonralar bu nəzəriyyədən istifadə edən digər alimlər arasında da bu ifadə tərzi yayılmağa başladı.
Qayda ondan ibarətdir ki, hər hansı növ tenzorlardan, koordinatlardan ibarət birhədlidə eyni simvol həm alt indeks, həm də üst indeks kimi yazılırsa, bu, o birhədlidə həmin indeks üzrə bütün komponentlərin bir-birilə cəmlənməsi anlamına gəlir:
— yerdəyişmə vektorunun koordinatını,
— yerdəyişmə koordinatını(),
m — koordinatların sayını göstərir.
Skalyar hasil
İki 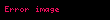
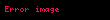

burada

wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Eynsteyn cemleme qaydasi Albert Eynsteyn terefinden Umumi Nisbilik Nezeriyyesi yazilarken daha qisa ve anlasiqli dilde cemleme emeliyyatini displaystyle sum ifade etmek meqsedile getirilib Sonralar bu nezeriyyeden istifade eden diger alimler arasinda da bu ifade terzi yayilmaga basladi Qayda ondan ibaretdir ki her hansi nov tenzorlardan koordinatlardan ibaret birhedlide eyni simvol hem alt indeks hem de ust indeks kimi yazilirsa bu o birhedlide hemin indeks uzre butun komponentlerin bir birile cemlenmesi anlamina gelir xaxa a 0mxaxa displaystyle x alpha x alpha sum alpha 0 m x alpha x alpha Bu x displaystyle vec x yerdeyisme vektoru ucun uzunlugun kvadrati x 2 displaystyle vec x 2 dusturu olub xa displaystyle x alpha x displaystyle vec x yerdeyisme vektorunun a displaystyle alpha koordinatini xa displaystyle x alpha x displaystyle tilde x yerdeyisme a displaystyle alpha koordinatini xa galxl displaystyle x alpha g alpha lambda x lambda m koordinatlarin sayini gosterir Skalyar hasilIki V V0 V1 V2 V3 displaystyle vec V V 0 V 1 V 2 V 3 ve U U0 U1 U2 U3 displaystyle vec U U 0 U 1 U 2 U 3 vektoru verilirse bu vektorlarin skalyar hasili Eynsteyn cemleme qaydasi ile daha qisa sekilde bele ifade olunar V U VaUa V0U0 V1U1 V2U2 V3U3 Ua galUl displaystyle vec V cdot vec U V alpha U alpha V 0 U 0 V 1 U 1 V 2 U 2 V 3 U 3 quad U alpha g alpha lambda U lambda burada gal displaystyle g alpha lambda metrik tenzordur Evklid fezasinin metrikasi diaqonal oldugundan ve sifirdan ferqli butun komponentleri vahide beraber oldugundan gab dba displaystyle g alpha beta delta beta alpha skalyar hasil V U V0U0 V1U1 V2U2 V3U3 displaystyle vec V cdot vec U V 0 U 0 V 1 U 1 V 2 U 2 V 3 U 3 formasini alir
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans