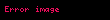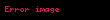Ellipsoid — Fəzada verilmiş hər hansı ortonormal reperinə nəzərən koordinatları
(1) tənliyini ödəyən fəzanın bütün nöqtələri çoxluğunun həndəsi yeri. (1) tənliyinə ellipsoidin kanonik tənliyi deyilir. Ellipsoidin kanonik tənliyindəki , və ədədləri müsbət həqiqi ədədlərdir. , və dəyişənləri (1) tənliyinə kvadratlarla daxil olduğundan ellipsoid ikitərtibli səthdir. Belə ki, səthin ikitərtibli olması üçün onun tənliyini ifadə edən çoxhədlinin dərəcəsi 2 olmalıdır. Burada isə (1) tənliyinin sol tərəfindəki ifadə ikidərəcəlidir. (1) tənliyində , və ədədləri cüt-cüt fərqli olarsa, (1) tənliyinə malik ellipsoidə üçoxlu ellipsoid deyilir. Ellipsoid ellipsin öz oxlarından biri ətrafında fırlanmasından da alına bilər ki, bu zaman həmin ellipsoidə fırlanma ellipsoidi deyilir. Fırlanma ellipsoidinin ortonormal reperinə nəzərən kanonik tənliyi
tənliyidir.
Aşağıdakı şəkildə (1) tənliyinə daxil olan , və ədədlərinin müxtəlif olduğu, 3-ü və ya 2-sinin bərabər olduğu hallarda ellipsoidin əyani təsviri verilmişdir.

sfera (a=b=c),
sferoid (a=b, c),
ellipsoid (a, b və c ədədləri cüt-cüt fərqli olduqda)
Əgər ellipsi böyük oxu ətrafında fırlatsaq, onda yumurtavari fiqur alınar. Əgər ellipsi kiçik oxu ərtafında fırlatsaq, onda yastılaşdırılmış sfera alınar. Yer kürəsi ellipsoid formasındadır. Yer kürəsinin qütbləri arasındakı məsafə (12714 km) onun ekvatorunun diametrinden (12756 km) kiçikdir.
Əgər fırlanma ellipsoidini ellipsin oxlarından keçən müstəviyə sıxsaq, onda üçoxlu ellipsoidi alarıq. Tənliyi isə yuxarıda göstərilmişdir.
Əgər ədədlərindən hər hansı ikisi bərabər olarsa, onda yuxarıdakı (1) tənliyi fırlanma ellipsoidini təsvir edir. Əgər (1) tənliyində == olarsa, onda həmin tənlik sferanı təsvir edir.
Əgər ellipsoid absis oxu , ordinat oxu və aplikat oxu olan düzbucaqlı dekart koordinat sistemində verilmişdirsə, onda həmin ellipsoidin oxu ilə kəsişmə nöqtələri və , oxu ilə kəsişmə nöqtələri və , oxu ilə kəsişmə nöqtələri isə və olar. , , , , və nöqtələrinə ellipsoidin təpə nöqtələri, , , parçalarına ellipsoidin oxları, həmin oxların kəsişmə nöqtəsinə isə ellipsoidin mərkəzi deyilir (onu da qeyd edək ki, (1) kanonik tənliyinə daxil olan , və ədədlərinə ellipsoidin yarımoxlarının uzunluqları deyilir). , və dəyişənləri ellipsoidin (1) tənliyinə kvadratlarla daxil olduğundan, əgər hər hansı cari nöqtəsi ellipsoidin (1) tənliyini ödəyirsə (başqa sözlə desək, nöqtəsi ellipsoidə aiddirsə), onda nöqtəsi ilə koordinat oxları, koordinat müstəviləri və koordinat başlanğıcına nəzərən simmetrik olan nöqtələr də bu tənliyi ödəyəcəklər (başqa sözlə desək, ellipsoidə aid olacaqlar). Deməli, ellipsoid koordinat oxlarına, koordinat müstəvilərinə və koordinat başlanğıcına nəzərən simmetrikdir. Üçoxlu ellipsoid üçün də analoji olaraq deyə bilərik ki, üçoxlu ellipsoidin istənilən oxunu saxlayan düz xətt onun simmetriya oxudur. Üçoxlu ellipsoidin ixtiyari iki oxundan keçən müstəvi onun simmetriya müstəvisidir. Üçoxlu ellipsoidin oxlarının kəsişmə nöqtəsi onun simmetriya mərkəzidir. Beləliklə, üçoxlu ellipsoidin üç simmetriya müstəvisi, üç simmetriya oxu, bir simmetriya mərkəzi var.
Ədəbiyyat
- M. Mərdanov, S. Mirzəyev, Ş. Sadıqov Məktəblinin riyaziyyatdan izahlı lüğəti. Bakı 2016, "Radius nəşriyyatı", 296 səh.
- Azərbaycan Sovet Ensiklopediyası. I–X cild, Bakı 1976–1987.
- X. Paşayev, M. Nəcəfov, Analitik həndəsədən mühazirələr. Bakı-2002.
İstinadlar
- İngiliscə vikipediya; https://en.m.wikipedia.org/wiki/Ellipsoid
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Ellipsoid Fezada verilmis her hansi R displaystyle R ortonormal reperine nezeren koordinatlarix2a2 y2b2 z2c2 1 displaystyle frac x 2 a 2 frac y 2 b 2 frac z 2 c 2 1 1 tenliyini odeyen fezanin butun noqteleri coxlugunun hendesi yeri 1 tenliyine ellipsoidin kanonik tenliyi deyilir Ellipsoidin kanonik tenliyindeki a displaystyle a b displaystyle b ve c displaystyle c ededleri musbet heqiqi ededlerdir x displaystyle x y displaystyle y ve z displaystyle z deyisenleri 1 tenliyine kvadratlarla daxil oldugundan ellipsoid ikitertibli sethdir Bele ki sethin ikitertibli olmasi ucun onun tenliyini ifade eden coxhedlinin derecesi 2 olmalidir Burada ise 1 tenliyinin sol terefindeki ifade ikiderecelidir 1 tenliyinde a displaystyle a b displaystyle b ve c displaystyle c ededleri cut cut ferqli olarsa 1 tenliyine malik ellipsoide ucoxlu ellipsoid deyilir Ellipsoid ellipsin oz oxlarindan biri etrafinda firlanmasindan da alina biler ki bu zaman hemin ellipsoide firlanma ellipsoidi deyilir Firlanma ellipsoidinin R displaystyle R ortonormal reperine nezeren kanonik tenliyix2a2 y2a2 z2c2 1 displaystyle frac x 2 a 2 frac y 2 a 2 frac z 2 c 2 1 tenliyidir Asagidaki sekilde 1 tenliyine daxil olan a displaystyle a b displaystyle b ve c displaystyle c ededlerinin muxtelif oldugu 3 u ve ya 2 sinin beraber oldugu hallarda ellipsoidin eyani tesviri verilmisdir 1 tenliyi ile teyin olunan ellipsoidler x2a2 y2b2 z2c2 1 displaystyle x 2 over a 2 y 2 over b 2 z 2 over c 2 1 sfera a b c sferoid a b c ellipsoid a b ve c ededleri cut cut ferqli olduqda Eger ellipsi boyuk oxu etrafinda firlatsaq onda yumurtavari fiqur alinar Eger ellipsi kicik oxu ertafinda firlatsaq onda yastilasdirilmis sfera alinar Yer kuresi ellipsoid formasindadir Yer kuresinin qutbleri arasindaki mesafe 12714 km onun ekvatorunun diametrinden 12756 km kicikdir Eger firlanma ellipsoidini ellipsin oxlarindan kecen musteviye sixsaq onda ucoxlu ellipsoidi alariq Tenliyi ise yuxarida gosterilmisdir Eger ededlerinden her hansi ikisi beraber olarsa onda yuxaridaki 1 tenliyi firlanma ellipsoidini tesvir edir Eger 1 tenliyinde a displaystyle a b displaystyle b c displaystyle c olarsa onda hemin tenlik sferani tesvir edir Eger ellipsoid absis oxu ox displaystyle ox ordinat oxu oy displaystyle oy ve aplikat oxu oz displaystyle oz olan duzbucaqli dekart koordinat sisteminde verilmisdirse onda hemin ellipsoidin ox displaystyle ox oxu ile kesisme noqteleri A a 0 0 displaystyle A a 0 0 ve A a 0 0 displaystyle A a 0 0 oy displaystyle oy oxu ile kesisme noqteleri B 0 b 0 displaystyle B 0 b 0 ve B 0 b 0 displaystyle B 0 b 0 oz displaystyle oz oxu ile kesisme noqteleri ise C 0 0 c displaystyle C 0 0 c ve C 0 0 c displaystyle C 0 0 c olar A displaystyle A A displaystyle A B displaystyle B B displaystyle B C displaystyle C ve C displaystyle C noqtelerine ellipsoidin tepe noqteleri AA displaystyle AA BB displaystyle BB CC displaystyle CC parcalarina ellipsoidin oxlari hemin oxlarin kesisme noqtesine ise ellipsoidin merkezi deyilir onu da qeyd edek ki 1 kanonik tenliyine daxil olan a displaystyle a b displaystyle b ve c displaystyle c ededlerine ellipsoidin yarimoxlarinin uzunluqlari deyilir x displaystyle x y displaystyle y ve z displaystyle z deyisenleri ellipsoidin 1 tenliyine kvadratlarla daxil oldugundan eger her hansi cari M x y z displaystyle M x y z noqtesi ellipsoidin 1 tenliyini odeyirse basqa sozle desek M x y z displaystyle M x y z noqtesi ellipsoide aiddirse onda M displaystyle M noqtesi ile koordinat oxlari koordinat mustevileri ve koordinat baslangicina nezeren simmetrik olan noqteler de bu tenliyi odeyecekler basqa sozle desek ellipsoide aid olacaqlar Demeli ellipsoid koordinat oxlarina koordinat mustevilerine ve koordinat baslangicina nezeren simmetrikdir Ucoxlu ellipsoid ucun de analoji olaraq deye bilerik ki ucoxlu ellipsoidin istenilen oxunu saxlayan duz xett onun simmetriya oxudur Ucoxlu ellipsoidin ixtiyari iki oxundan kecen mustevi onun simmetriya mustevisidir Ucoxlu ellipsoidin oxlarinin kesisme noqtesi onun simmetriya merkezidir Belelikle ucoxlu ellipsoidin uc simmetriya mustevisi uc simmetriya oxu bir simmetriya merkezi var EdebiyyatM Merdanov S Mirzeyev S Sadiqov Mekteblinin riyaziyyatdan izahli lugeti Baki 2016 Radius nesriyyati 296 seh Azerbaycan Sovet Ensiklopediyasi I X cild Baki 1976 1987 X Pasayev M Necefov Analitik hendeseden muhazireler Baki 2002 IstinadlarIngilisce vikipediya https en m wikipedia org wiki Ellipsoid
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State




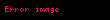


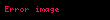
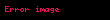

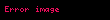

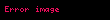
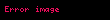










![{\displaystyle [AA']}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4MVpEaGtNR1V6TURCaVpHRTFZMkpsTnpBNE4yVmxPRFpqTVRRMVl6RTJaamRsTlRGbFpqSmsuc3Zn.svg)
![{\displaystyle [BB']}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4MU9UUTROemN4WVdZNE9Ea3dNakJrTnpZMlptSmlaamMzT1RJMk0yTmlabVF4WkdFeVlXRTEuc3Zn.svg)
![{\displaystyle [CC']}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4M01UQmtNR1F5TWpVeU9HVXhZbVkxWldJM056WTNZVEJpT0dabVltSTRNakZrWkdNellqVTAuc3Zn.svg)