Dürasiya

Dürasiya (ing. duration — "müddəti") — ödənişlər axınının orta çəkili müddəti. Çəkilər ödənişlərin diskont edilmiş dəyəridir. Dürasiya pul vəsaitlərinin hərəkətinin ən vacib xarakteristikasıdır ki, bu da onun cari dəyərinin faiz dərəcəsinin dəyişməsinə həssaslığını müəyyən edir. Bir axının dürasiyası təkcə onun strukturundan deyil, həm də cari faiz dərəcəsindən asılıdır. Faiz nə qədər yüksək olarsa, qısamüddətli ödənişlərə nisbətən uzunmüddətli ödənişlərin dəyərinin payı bir o qədər az olar və müddəti nə qədər qısa olarsa, əksinə, dərəcə nə qədər aşağı olarsa, ödəniş axınının müddəti də bir o qədər çox olar.

Dürasiya anlayışını amerikalı alim F. R. Makoli təqdim etmişdir.

Mahiyyəti

Dürasiya — çəkili orta

Qeyri-opsion istiqrazlarının müddəti orta çəkili düsturla aşağıdakı kimi hesablanır:

${\displaystyle D={\overline {T}}={\frac {\sum _{i}\ PV_{i}\cdot t_{i}}{\sum _{i}PV_{i}}}={\frac {\sum _{i}{\frac {CF_{i}}{(1+r)^{t_{i}}}}\cdot t_{i}}{\sum _{i}{\frac {CF_{i}}{(1+r)^{t_{i}}}}}}}$

və ya

${\displaystyle D={\overline {T}}={\frac {\sum _{i}{CF_{i}}\cdot {e}^{-{r_{c}}{t_{i}}}\cdot t_{i}}{\sum _{i}{CF_{i}}\cdot {e}^{-{r_{c}}{t_{i}}}}},}$

burada:

${\displaystyle CF_{i}}$ — ${\displaystyle i}$ ödəniş;

${\displaystyle r}$ — diskont dərəcəsi, vaxt vahidinə (il, rüb və s.) alternativ investisiyanın gəlirliliyi;

${\displaystyle r_{c}}$ — davamlı faiz hesablanması üçün diskont dərəcəsi;

${\displaystyle PV_{i}}$ — i-ci ödənişin güzəştli dəyəri;

${\displaystyle t_{i}}$ — i-ci ödənişin vaxtı;

Bu düsturun məxrəci verilmiş diskont dərəcəsi ilə pul vəsaitlərinin hərəkətinin cari dəyərinin təxminidir. Əgər pul vəsaitlərinin hərəkəti cari qiymətin bazar (və ya digər) qiymətləndirilməsi 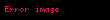${\displaystyle P}$ olan maliyyə aləti tərəfindən yaradılırsa, bu halda diskont dərəcəsi bu alətin daxili gəlir dərəcəsidir (istiqrazlar üçün — ödəmə müddətinə qədər gəlir). Bu nisbət bərabərlik əsasında müəyyən edilir

${\displaystyle P=PV(r)=\sum _{i}{\frac {CF_{i}}{(1+r)^{t_{i}}}}.}$

Ehtimal edilir ki, bazar tələb olunan uçot dərəcəsini effektiv şəkildə müəyyən edir və oxşar risk səviyyəsinə malik alətlər üzrə tələb olunan gəliri əks etdirir.

Faiz dərəcəsi riski

Əgər pul vəsaitlərinin hərəkətinin cari dəyərini faiz dərəcəsinin funksiyası kimi nəzərdən keçirsək, onda pul vəsaitlərinin hərəkətinin müddəti faiz dərəcəsi üzrə (və ya ekvivalent olaraq, 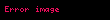${\displaystyle 1+r}$), yəni

${\displaystyle D=-{\frac {d\ln PV}{d\ln(1+r)}}=-{\frac {dPV/PV}{d(1+r)/(1+r)}}=-{\frac {1+r}{PV}}{\frac {dPV}{dr}}.}$

Nəticədə,

${\displaystyle dPV/PV=-Dd\ln(1+r)=-Ddr/(1+r).}$

Tariflərdə kiçik dəyişikliklər üçün diferensiallar sadə dəyişikliklərlə əvəz edilə bilər:

${\displaystyle \delta PV=\Delta PV/PV\approx =-D\delta r=-D\Delta r/(1+r).}$

Beləliklə, dürasiya alətin bazar qiymətinin faiz dərəcəsinin dəyişməsindən asılılıq dərəcəsinin sadələşdirilmiş qiymətləndirilməsinə imkan verir. Alətin müddəti nə qədər uzun olarsa, faiz dərəcələri dəyişdikdə onun bazar dəyəri bir o qədər çox olar, yəni faiz dərəcəsi riski bir o qədər yüksək olar.

Dəyişdirilmiş dürasiya

Yuxarıdakı təxmini bərabərlikdə dəyişdirilmiş müddətə bərabər olan sözdə istifadə edirik

${\displaystyle MD=-{\frac {d\ln PV}{dr}}=D/(1+r),}$

faiz dərəcəsi həssaslığının qiymətləndirilməsi sadələşdirilmişdir:

${\displaystyle \delta PV\approx -MD\cdot \Delta r.}$

Şərhi

(Dəyişdirilmiş) müddətdən istifadə etməklə pul vəsaitlərinin hərəkətinin ədalətli dəyərindəki mümkün dəyişikliyi qiymətləndirərkən bu təxminin təxmini xarakteri nəzərə alınmalıdır. Üstəlik, kəmiyyət qeyri-dəqiqlikləri ilə yanaşı, həqiqi asılılıq ilə müddət və ya dəyişdirilmiş müddətin köməyi ilə xəttiləşdirilmiş keyfiyyət fərqi də mövcuddur: faiz dərəcəsində eyni müsbət və mənfi dəyişikliklər eyni mütləq dəyərdə qiymət dəyişikliyinə təsir göstərir. Reallıqda bu belə deyil — qiymət artımı və azalan dərəcələrlə asimmetrik şəkildə dəyişir, yəni dərəcəsin aşağı salınması dərəcəsi eyni mütləq dəyərə qaldırarkən qiyməti aşağı salmaqdan daha çox qiymət artımına gətirib çıxarır. Aydınlaşdırma məqsədilə (həm kəmiyyət, həm də keyfiyyət), müddətlə yanaşı, pul vəsaitlərinin hərəkətinin ikinci dərəcəli düzəliş olan sözdə qabarıqlığından da istifadə olunur. Qiymət dəyişikliyinə bu düzəliş məzənnə dəyişikliyinin kvadratından asılıdır (yəni işarədən asılı deyil), ona görə də dərəcələr artdıqda, müddətlə proqnozlaşdırılan qiymət enişinin dərəcəsini azaldır, dərəcə azaldıqda isə müddəti ilə təxmin edilən artımı artırır. Beləliklə, asimmetriya da nəzərə alınır və təxmin kəmiyyətcə dəqiqləşdirilir.

Daha dəqiq qiymətləndirmənin başqa bir versiyası, keyfiyyət qeyri-dəqiqliyinin təkcə xəttiləşdirmə ilə deyil (və o qədər də çox deyil), həm də loqarifmlərdəki dəyişikliklərin adi artım templəri ilə əvəz edilməsi ilə əlaqəli olduğuna əsaslanır. Əgər loqarifmlərin özündən istifadə etsək, onda qiymətləndirmələr keyfiyyətcə həqiqi asılılığa daha adekvat olacaq (baxmayaraq ki, kəmiyyət qeyri-dəqiqliyi də olacaq):

${\displaystyle \Delta \ln PV=-D\Delta \ln(1+r).}$

Bu nisbətdən cari dəyərdəki dəyişikliyin aşağıdakı daha doğru təxmini asılılığı əldə edilir:

${\displaystyle \delta PV\approx (1+\Delta r/(1+r))^{-D}-1.}$

İstinadlar

1. "Macaulay Duration, Money Duration and Modified Duration". cfastudyguide.com. cfastudyguide.com. 28 March 2022 tarixində arxivləşdirilib. İstifadə tarixi: 10 December 2021.
2. Hull, John C., Options, Futures, and Other Derivative Securities (Second), Englewood Cliffs, NJ: Prentice-Hall, Inc., 1993, 99–101
3. Brealey, Richard A.; Myers, Stewart C.; Allen, Franklin, (Tenth), New York, NY: McGraw-Hill Irwin, 2011, 50–53