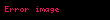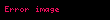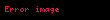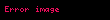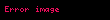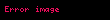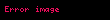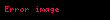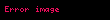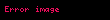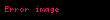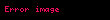Dispersiya təsadüfi dəyişənin sıçrama ölçüsüdür, yəni onun riyazi gözləmədən meyillənməsidir. O, ilə işarə olunur. Statistikada çox vaxt və ya işarələmələrindən istifadə edilir. Dispersiyanın kökü, yəni orta kvadratik meyillənmə adlanır. Standart meyillənmə də təsadüfi qiymətin vahidi ilə ölçülür. Dispersiya isə bu vahidin kvadratı ilə göstərilir.
Təyinatı
Tutaq ki, 
burada M göstərir.
Qeyd
- Əgər təsadüfi qiymət
həqiqi ədədlərdirsə, onda riyazi gözləmənin xətti olması əsasında aşağıdakı düstur düzgündür:
- Dispersiya təsadüfi qiymətin mərkəzi momenti sayılır;
- Disperisya sonsuz ola bilər. Məsələn .
- Disperisya moment funksiya yaradıcılarının köməyi ilə hesablana bilir
:
- Y1...Yn təsadüfi ardıcıllığın dispersiyasının riyazi gösləməsi belə hesablanır:
Xassələri
- İstənilən təsadüfi qiymətlərin disperisyası müsbətdir:
- Əgər təsadüfi qiymətlərin disperisyası sonludursa,onda onun riyazi gözləməsi də sonludur;
- Əgər təsadüfi qiymət konstanta bərabərdirsə, onda onun dispersiya sıfırdır:
Əksinə mülahizə də doğrudur: əgər
olrsa, onda
;
- İki təsadüfi qiymətlərin cəminin dispersiyası bərabərdir:
, burada
— onların ;
- Bir neçə təsadüfi qiymətlərin xətti kombinasiyasının istənilən disperisyası üçün aşağıdakı bərabərlik doğrudur:
, burada
;
- Xüsusi halda, istənilən asılı olmayan və ya korrelyasiya olmayan təsadüfi qiymətlər üçün bu düsturdan istifadə edilir:
çünki, onların kovariyasiyası sıfıra bərabərdir;
Mənbə
- 1.Колмогоров А.Н. Глава IV. Математические ожидания; §3. Неравенство Чебышева // Основные понятия теории вероятностей. — 2-е изд. — М.: Наука, 1974. — С. 63—65. — 120 с.
- 2.Боровков А.А. Глава 4. Числовые характеристики случайных величин; §5. Дисперсия // Теория вероятностей. — 5-е изд. — М.: Либроком, 2009. — С. 93-94. — 656 с.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Dispersiya tesadufi deyisenin sicrama olcusudur yeni onun riyazi gozlemeden meyillenmesidir O D X displaystyle D X ile isare olunur Statistikada cox vaxt sX2 displaystyle sigma X 2 ve ya s2 displaystyle displaystyle sigma 2 isarelemelerinden istifade edilir Dispersiyanin koku yeni s displaystyle displaystyle sigma orta kvadratik meyillenme adlanir Standart meyillenme de tesadufi qiymetin vahidi ile olculur Dispersiya ise bu vahidin kvadrati ile gosterilir TeyinatiTutaq ki X displaystyle X tesadufi qiymetdir onda D X M X M X 2 displaystyle D X M left X M X 2 right burada M gosterir QeydEger tesadufi qiymet X displaystyle X heqiqi ededlerdirse onda riyazi gozlemenin xetti olmasi esasinda asagidaki dustur duzgundur D X M X2 M X 2 displaystyle D X M X 2 left M X right 2 Dispersiya tesadufi qiymetin merkezi momenti sayilir Disperisya sonsuz ola biler Meselen Disperisya moment funksiya yaradicilarinin komeyi ile hesablana bilir U t displaystyle U t D X M X2 M X 2 U 0 U 0 2 displaystyle D X M X 2 left M X right 2 U 0 left U 0 right 2 Y1 Yn tesadufi ardicilligin dispersiyasinin riyazi goslemesi bele hesablanir D i 1nYi2 i 1nYi 2nn 1 displaystyle D dfrac sum i 1 n Y i 2 dfrac left sum i 1 n Y i right 2 n n 1 XasseleriIstenilen tesadufi qiymetlerin disperisyasi musbetdir D X 0 displaystyle D X geqslant 0 Eger tesadufi qiymetlerin disperisyasi sonludursa onda onun riyazi gozlemesi de sonludur Eger tesadufi qiymet konstanta beraberdirse onda onun dispersiya sifirdir D a 0 displaystyle D a 0 Eksine mulahize de dogrudur eger D X 0 displaystyle D X 0 olrsa onda X M X displaystyle X M X Iki tesadufi qiymetlerin ceminin dispersiyasi beraberdir D X Y D X D Y 2cov X Y displaystyle D X Y D X D Y 2 text cov X Y burada cov X Y displaystyle text cov X Y onlarin Bir nece tesadufi qiymetlerin xetti kombinasiyasinin istenilen disperisyasi ucun asagidaki beraberlik dogrudur D i 1nciXi i 1nci2D Xi 2 1 i lt j ncicjcov Xi Xj displaystyle D left sum i 1 n c i X i right sum i 1 n c i 2 D X i 2 sum 1 leqslant i lt j leqslant n c i c j text cov X i X j burada ci R displaystyle c i in mathbb R Xususi halda istenilen asili olmayan ve ya korrelyasiya olmayan tesadufi qiymetler ucun bu dusturdan istifade edilir D X1 Xn D X1 D Xn displaystyle D X 1 X n D X 1 D X n cunki onlarin kovariyasiyasi sifira beraberdir D aX a2D X displaystyle D left aX right a 2 D X D X D X displaystyle D left X right D X D X b D X displaystyle D left X b right D X Menbe1 Kolmogorov A N Glava IV Matematicheskie ozhidaniya 3 Neravenstvo Chebysheva Osnovnye ponyatiya teorii veroyatnostej 2 e izd M Nauka 1974 S 63 65 120 s 2 Borovkov A A Glava 4 Chislovye harakteristiki sluchajnyh velichin 5 Dispersiya Teoriya veroyatnostej 5 e izd M Librokom 2009 S 93 94 656 s
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State