Düz xətt — həndəsənin əsas elementlərindən biridir. Həndəsənin sistematik təsviri zamanı düz xətt yalnız birbaşa olmayan şəkildə aksiomalarla təsbit edilir.

Düz xəttin aşağıdakı xassələri vardır:
- İki üst-üstə düşməyən nöqtədən yalnız bir düz xətt keçirmək olar.
- Müstəvi üzərində üst-üstə düşməyən iki düz xətt ya bir nöqtədə kəsişir, ya da paraleldir.
Üçölçülü fəzada iki düz xəttin qarşılıqlı vəziyyətini təsvir etmək üçün 4 variant mövcuddur:
- düz xətlər paraleldirlər;
- düz xətlər kəsişirlər;
- düz xətlər perpendikulyardırlar;
- düz xətlər çarpazdır;
Dekart koordinat sistemində düz xətti birdərcəli tənliklə ifadə etmək olur.
Kəsişən düz xətlər
Müstəvi üzərində iki müxtəlif düz xəttin bir ortaq nöqtəsi olarsa, onda deyirlər ki, bu düz xətlər kəsişir.
Paralel düz xətlər
Bir müstəvi üzərində üst-üstə düşməyən və kəsişməyən düz xətlər paralel düz xətlər adlanır.
Çarpaz düz xətlər
Fəzada paralel olmayan və kəsişməyən iki düz xətt çarpaz düz xətlər adlanır.
Düz xətt tənlikləri
Düz xəttin bucaq əmsalı tənliyi

OX oxuna perpendikulyar olmayan hər hansı düz xəttin verilməsini fərz edək. Bu düz xəttin absis oxu ilə əmələ gətirdiyi bucaq φ, ordinat oxundan ayırdığı parça 
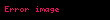
Burada 

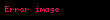



Əgər düz xətt absis oxuna perpendikulyar olarsa, onda 


Düz xəttin ümumi tənliyi
XOY sistemində bir düz xətti təyin edən ümumi tənlik aşağıdakı kimidir:

Burada müxtəlif hallar mümkündür. Aşağıdakı cədvəl bu halları əhatə edir.
| Əmsalların qiymətləri | Düz xəttin tənliyi | Düz xəttin vəziyyəti | |
|---|---|---|---|
| 1 |  , ,  , , 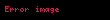 |    | İxtiyari düz xətt |
| 2 | 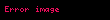 |  | Düz xətt koordinat başlanğıcından keçir |
| 3 |  |  , , 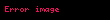 | OX oxuna paralele düz xətt |
| 4 |  |  | OY oxuna paralel düz xətt |
| 5 | 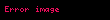 |  | OX oxu üzərinə düşən düz xətt |
| 6 |  |  | OY oxu üzərinə düşən düz xətt |
Düz xəttin parçalarla tənliyi

Şəkildə göstərildiyi kimi düz xətt koordinat oxlardan uyğun olaraq 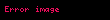
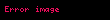


Belə halda 
Həmçinin bax
İstinadlar
- Səlimov, Fazil; Zülfüqarov, Eldar. Ali Riyaziyyat I. Bakı: Çaşıoğlu. 2001. səh. 32-33. (#accessdate_missing_url)
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Duz xett hendesenin esas elementlerinden biridir Hendesenin sistematik tesviri zamani duz xett yalniz birbasa olmayan sekilde aksiomalarla tesbit edilir Duz xetler Duz xettin asagidaki xasseleri vardir Iki ust uste dusmeyen noqteden yalniz bir duz xett kecirmek olar Mustevi uzerinde ust uste dusmeyen iki duz xett ya bir noqtede kesisir ya da paraleldir Ucolculu fezada iki duz xettin qarsiliqli veziyyetini tesvir etmek ucun 4 variant movcuddur duz xetler paraleldirler duz xetler kesisirler duz xetler perpendikulyardirlar duz xetler carpazdir Dekart koordinat sisteminde duz xetti birderceli tenlikle ifade etmek olur Kesisen duz xetlerMustevi uzerinde iki muxtelif duz xettin bir ortaq noqtesi olarsa onda deyirler ki bu duz xetler kesisir Paralel duz xetlerBir mustevi uzerinde ust uste dusmeyen ve kesismeyen duz xetler paralel duz xetler adlanir Carpaz duz xetlerFezada paralel olmayan ve kesismeyen iki duz xett carpaz duz xetler adlanir Duz xett tenlikleriDuz xettin bucaq emsali tenliyi Duz xettin bucaq emsali tenliyinin sekli OX oxuna perpendikulyar olmayan her hansi duz xettin verilmesini ferz edek Bu duz xettin absis oxu ile emele getirdiyi bucaq f ordinat oxundan ayirdigi parca OB b displaystyle OB b olsun Duz xett uzerinde sekildeki kimi ixtiyari M x y noqtesi goturek Bu zaman tan f y bx 0 displaystyle tan varphi frac y b x 0 Burada tan f k displaystyle tan varphi k oldugunu nezere alsaq y kx b displaystyle y kx b olar Sonuncu tenliye duz xettin bucaq emsali tenliyi deyilir k 0 displaystyle k 0 olduqda tan f 0 displaystyle tan varphi 0 olur ve belelikle de f 0 displaystyle varphi 0 olur Bu halda duz xett absis oxuna paralel olur ve duz xett tenliyi y b displaystyle y b seklinde olur Bu ise ordinat oxundan b uzunluqda parca ayirib absis oxuna paralel olan duz xettin tenliyidir Eger duz xett absis oxuna perpendikulyar olarsa onda f p2 displaystyle varphi frac pi 2 olur bu halda ise k tan p2 displaystyle k tan frac pi 2 olacaq yeni k nin bu qiymeti teyin edilmemisdir Bu halda duz xettin butun noqtelerinin basisleri eynidir ve duz xettin tenliyi x a displaystyle x a seklinde olur Belelikle butun hallarda duz xett x ve y lere nezeren birdereceli tenlikle xarakterize olunur Duz xettin umumi tenliyi XOY sisteminde bir duz xetti teyin eden umumi tenlik asagidaki kimidir Ax By C 0 displaystyle Ax By C 0 Burada muxtelif hallar mumkundur Asagidaki cedvel bu hallari ehate edir Emsallarin qiymetleri Duz xettin tenliyi Duz xettin veziyyeti1 A 0 displaystyle A neq 0 B 0 displaystyle B neq 0 C 0 displaystyle C neq 0 Ax By C 0 displaystyle Ax By C 0 displaystyle Rightarrow y kx b displaystyle y kx b Ixtiyari duz xett2 C 0 displaystyle C 0 Ax By 0 y ABx displaystyle Ax By 0 Rightarrow y frac A B x Duz xett koordinat baslangicindan kecir3 A 0 displaystyle A 0 y b displaystyle y b b CB displaystyle b frac C B OX oxuna paralele duz xett4 B 0 displaystyle B 0 x a a CA displaystyle x a a frac C A OY oxuna paralel duz xett5 C 0 displaystyle C 0 y 0 displaystyle y 0 OX oxu uzerine dusen duz xett6 B C 0 displaystyle B C 0 x 0 displaystyle x 0 OY oxu uzerine dusen duz xettDuz xettin parcalarla tenliyi Duz xettin parcalarla tenliyinin alinmasi Sekilde gosterildiyi kimi duz xett koordinat oxlardan uygun olaraq a 0 b 0 displaystyle a neq 0 b neq 0 parcalarini kesib kecir Onda A a 0 displaystyle a 0 B 0 b displaystyle 0 b olar Bu noqteleri nezere alaraq Duz xettin parcalarla tenliyi asagidaki kimi verilir xa yb 1 a 0 b 0 displaystyle frac x a frac y b 1 quad a neq 0 b neq 0 Bele halda Oy displaystyle Oy xettine paralel olan duz xett almaq mumkun olmur Hemcinin baxCepeki xettIstinadlarSelimov Fazil Zulfuqarov Eldar Ali Riyaziyyat I Baki Casioglu 2001 seh 32 33 accessdate missing url
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State