Çoxluqlar nəzəriyyəsi – riyaziyyatın çoxluqların ümumi xassələrini öyrənən bölməsi. Bir çox riyazi fənlər, o cümlədən cəbr, riyazi analiz, ölçü nəzəriyyəsi, stoxastik və topologiya çoxluq nəzəriyyəsinə əsaslanırlar. Əsası alman riyaziyyatçısı Qeorq Kantor tərəfindən qoyulmuşdur.
Anlayışlar
Hər hansı bir çoxluğu təşkil edən obyektlərə bu çoxluğun elementi deyilir. Çoxluqlar böyük hərflərlə, çoxluğun elementləri isə uyğun kiçik hərflərlə işarə olunur.
Çoxluq nəzəriyyəsində 





Alt Çoxluğu

Bir çoxluq 





- .
Bərabərlik
İki çoxluq o zaman bərabərdirlər ki, onlar eyni elementlərə malik olsunlar.
Bu analyış çoxluq nəzəriyyəsinin əsası hesab olunur. Formal olaraq belə ifadə olunur:
Boş çoxluq
Tərkibində heç bir element olmayan çoxluq boş çoxluq adlanır. O 
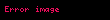
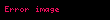

— A çoxluğunun boş alt çoxluğudur. Aşkar
Çoxluqların kəsişməsi

 və
və  -nin kəsişmə çoxluğu
-nin kəsişmə çoxluğuA və B çoxluqlarının hər ikisinə eyni zamanda daxil olan bütün elementlərdən ibarət olan C çoxluğuna bu çoxluqların kəsişməsi deyilir:
Bir qeyri-xətti 
Çoxluqların birləşməsi
- A və B çoxluqlarından heç olmasa birinə daxil olan bütün elementlərdən ibarət olan C çoxluğuna bu çoxluqların birləşməsi deyilir və simvolik olaraq А U В kimi işarə olunur. Başqa sözlə, A və B çoxluqlarından birləşməsi nəticəsində alınan yeni C çoxluğunda hər iki çoxluğun bütünü elementləri daxildir. Çoxluqların birləşməsini rəqəmlər çoxluqları üzərində göstərək: Fərz edək ki, A çoxluğu 1,2,3,4 rəqəmlərindən ibarətdir, B çoxluğu isə 3,4,5,6 rəqəmlərindən ibarətdir. Bu iki çoxluğun birləşməsi 1,2,3,4,5,6 rəqəmindən ibarət yeni çoxluq olacaq, çünki 3 və 4 rəqəmləri A çoxluğunda da, B çoxluğunda da var və tam olaraq həm A, həm də B çoxluğu nəticədə alınan çoxluğa daxildir. Əgər А={1,2,3,4}, B={3,4,5,6}, onda A U B = {1,2,3,4,5,6}:A və B çoxluqlarından heç olmasa birinə daxil olan bütün elementlərdən ibarət olan C çoxluğuna bu çoxluqların birləşməsi deyilir və simvolik olaraq А U В kimi işarə olunur. Başqa sözlə, A və B çoxluqlarından birləşməsi nəticəsində alınan yeni C çoxluğunda hər iki çoxluğun bütünü elementləri daxildir. Çoxluqların birləşməsini rəqəmlər çoxluqları üzərində göstərək: Fərz edək ki, A çoxluğu 1,2,3,4 rəqəmlərindən ibarətdir, B çoxluğu isə 3,4,5,6 rəqəmlərindən ibarətdir. Bu iki çoxluğun birləşməsi 1,2,3,4,5,6 rəqəmindən ibarət yeni çoxluq olacaq, çünki 3 və 4 rəqəmləri A çoxluğunda da, B çoxluğunda da var və tam olaraq həm A, həm də B çoxluğu nəticədə alınan çoxluğa daxildir. Əgər А={1,2,3,4}, B={3,4,5,6}, onda A U B = {1,2,3,4,5,6}:
.

 və
və  çoxluqlarından yaranmış birləşim çoxluğu
çoxluqlarından yaranmış birləşim çoxluğuƏdəbiyyat
- Николя Бурбаки. Основания математики. Логика. Теория множеств // Очерки по истории математики. Элементы математики. М: Издательство иностранной литературы. Башмакова, Изабелла Григорьевна (перевод с французского). 1963. 37–53.
- Г. Кантор. Труды по теории множеств. Классики науки (3450 nüs.). М.: Наука. 1985..
- Коэн, Пол Джозеф. Об основаниях теории множеств (PDF). XXIX (Успехи математических наук). М. Манин, Юрий Иванович (перевод). 1974 [P. J. Cohen, Comments on the foundations of set theory, Proc. Sym. Pure Math. 13:1 (1971), 9–15.] 169–176.
- Куратовский, Казимир, Мостовский, Анджей. Теория множеств. М.: Мир. Перевод с английского М. И. Кратко под редакцией А. Д. Тайманова. 1970.
- Медведев, Фёдор Андреевич. Развитие теории множеств в XIX веке (2500 nüs.). М.: Наука. 1965.
- Френкель, Адольф, И. Бар-Хиллел. Основания теории множеств. М.: Мир. Перевод с английского Ю. А. Гастева под редакцией Есенин-Вольпин, Александр Сергеевич. 1966.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Coxluqlar nezeriyyesi riyaziyyatin coxluqlarin umumi xasselerini oyrenen bolmesi Bir cox riyazi fenler o cumleden cebr riyazi analiz olcu nezeriyyesi stoxastik ve topologiya coxluq nezeriyyesine esaslanirlar Esasi alman riyaziyyatcisi Qeorq Kantor terefinden qoyulmusdur AnlayislarHer hansi bir coxlugu teskil eden obyektlere bu coxlugun elementi deyilir Coxluqlar boyuk herflerle coxlugun elementleri ise uygun kicik herflerle isare olunur Coxluq nezeriyyesinde a A displaystyle a in A munasibeti o demekdir ki a displaystyle a A displaystyle A coxlugunun elementidir Bunun inkari ise a A displaystyle a notin A kimi isare edililirler Bu munasibet ise onu gosterir ki a displaystyle a A displaystyle A coxlugunun elementi deyil Alt Coxlugu A coxlugu B nin altcoxlugudur Bir coxluq A displaystyle A diger coxlugun B displaystyle B o vaxt altcoxlugu adlanir ki A displaystyle A coxluguna aid olan ixtiyari element hem de B displaystyle B coxlugunun elementi olsun B displaystyle B o zaman A displaystyle A nin ustcoxlugu adlanir Formal olaraq A B x x A x B displaystyle A subseteq B Longleftrightarrow forall x left x in A rightarrow x in B right Beraberlik Iki coxluq o zaman beraberdirler ki onlar eyni elementlere malik olsunlar Bu analyis coxluq nezeriyyesinin esasi hesab olunur Formal olaraq bele ifade olunur A B x x A x B displaystyle A B Longleftrightarrow forall x left x in A leftrightarrow x in B right Bos coxluq Terkibinde hec bir element olmayan coxluq bos coxluq adlanir O displaystyle varnothing ve ya displaystyle ile isare olunur Beraberlik qanunundan alinir ki yalniz bir nir bos coxluq movcuddur Diger bos coxluqlar ele hemin elementleri ehate edirler yeni beraberdirler Uygun olaraq displaystyle emptyset ve displaystyle emptyset muxtelif olurlar Cunki sonuncu coxluq birinciden ferqli olan elemente sahibdir Bos coxluq her bir coxlugun alt coxlugudur Bos coxlugu hemcinin asagidaki kimi de ifade etmek olar A x A x A displaystyle emptyset A x in A mid forall x notin A A displaystyle emptyset A A coxlugunun bos alt coxlugudur AskarCoxluqlarin kesismesi A displaystyle A ve B displaystyle B nin kesisme coxlugu A ve B coxluqlarinin her ikisine eyni zamanda daxil olan butun elementlerden ibaret olan C coxluguna bu coxluqlarin kesismesi deyilir Bir qeyri xetti U displaystyle U coxlugu verilir Bu coxluqdan yaranmis kesisme coxlugu A ve B coxluqlarina aid olan elemntlerden teskil olunur Daha deqiq desek A ve B coxluqlarinin kesismesinden yaranan coxlugun elementleri bu her iki coxlugun altcoxlugudur Formal olaraq U x a U x a displaystyle bigcap U x mid forall a in U x in a Coxluqlarin birlesmesi A ve B coxluqlarindan hec olmasa birine daxil olan butun elementlerden ibaret olan C coxluguna bu coxluqlarin birlesmesi deyilir ve simvolik olaraq A U V kimi isare olunur Basqa sozle A ve B coxluqlarindan birlesmesi neticesinde alinan yeni C coxlugunda her iki coxlugun butunu elementleri daxildir Coxluqlarin birlesmesini reqemler coxluqlari uzerinde gosterek Ferz edek ki A coxlugu 1 2 3 4 reqemlerinden ibaretdir B coxlugu ise 3 4 5 6 reqemlerinden ibaretdir Bu iki coxlugun birlesmesi 1 2 3 4 5 6 reqeminden ibaret yeni coxluq olacaq cunki 3 ve 4 reqemleri A coxlugunda da B coxlugunda da var ve tam olaraq hem A hem de B coxlugu neticede alinan coxluga daxildir Eger A 1 2 3 4 B 3 4 5 6 onda A U B 1 2 3 4 5 6 A ve B coxluqlarindan hec olmasa birine daxil olan butun elementlerden ibaret olan C coxluguna bu coxluqlarin birlesmesi deyilir ve simvolik olaraq A U V kimi isare olunur Basqa sozle A ve B coxluqlarindan birlesmesi neticesinde alinan yeni C coxlugunda her iki coxlugun butunu elementleri daxildir Coxluqlarin birlesmesini reqemler coxluqlari uzerinde gosterek Ferz edek ki A coxlugu 1 2 3 4 reqemlerinden ibaretdir B coxlugu ise 3 4 5 6 reqemlerinden ibaretdir Bu iki coxlugun birlesmesi 1 2 3 4 5 6 reqeminden ibaret yeni coxluq olacaq cunki 3 ve 4 reqemleri A coxlugunda da B coxlugunda da var ve tam olaraq hem A hem de B coxlugu neticede alinan coxluga daxildir Eger A 1 2 3 4 B 3 4 5 6 onda A U B 1 2 3 4 5 6 U x x A textstyle bigcap U x mid forall x notin A A displaystyle A ve B displaystyle B coxluqlarindan yaranmis birlesim coxluguEdebiyyatNikolya Burbaki Osnovaniya matematiki Logika Teoriya mnozhestv Ocherki po istorii matematiki Elementy matematiki M Izdatelstvo inostrannoj literatury Bashmakova Izabella Grigorevna perevod s francuzskogo 1963 37 53 G Kantor Trudy po teorii mnozhestv Klassiki nauki 3450 nus M Nauka 1985 Koen Pol Dzhozef Ob osnovaniyah teorii mnozhestv PDF XXIX Uspehi matematicheskih nauk M Manin Yurij Ivanovich perevod 1974 P J Cohen Comments on the foundations of set theory Proc Sym Pure Math 13 1 1971 9 15 169 176 Kuratovskij Kazimir Mostovskij Andzhej Teoriya mnozhestv M Mir Perevod s anglijskogo M I Kratko pod redakciej A D Tajmanova 1970 Medvedev Fyodor Andreevich Razvitie teorii mnozhestv v XIX veke 2500 nus M Nauka 1965 Frenkel Adolf I Bar Hillel Osnovaniya teorii mnozhestv M Mir Perevod s anglijskogo Yu A Gasteva pod redakciej Esenin Volpin Aleksandr Sergeevich 1966
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State