1. Qamma-funksiya


Qamma-funksiyasının əsas xassəsi
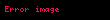
düsturu ilə ifadə olunur. Əgər 
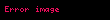

2. Tamamlama düsturu


Bu düstur arqumentin mənfi qiymətləri üçün qamma-funksiyasını təyin etməyə imkan verir.
3. Beta-funksiya




düsturu dogrudur
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
1 Qamma funksiyax gt 0 displaystyle x gt 0 olduqda G x 0 tx 1e tdt displaystyle Gamma x int limits 0 infty t x 1 e t dt Qamma funksiyasinin esas xassesi G x 1 xG x displaystyle Gamma x 1 x Gamma x dusturu ile ifade olunur Eger n displaystyle n natural ededdirse onda G n n 1 displaystyle Gamma n n 1 G n 12 1 3 2n 1 2np displaystyle Gamma n tfrac 1 2 tfrac 1 times 3 2n 1 2 n sqrt pi 2 Tamamlama dusturux displaystyle x tam ededden ferqli olduqda G x G 1 x psin px displaystyle Gamma x Gamma 1 x tfrac pi sin pi x Bu dustur arqumentin menfi qiymetleri ucun qamma funksiyasini teyin etmeye imkan verir 3 Beta funksiyax gt 0 displaystyle x gt 0 ve y gt 0 displaystyle y gt 0 olduqda B x y 01tx 1 1 t y 1dt displaystyle mathrm B x y int limits 0 1 t x 1 1 t y 1 dt B x y G x G y G x y displaystyle mathrm B x y tfrac Gamma x Gamma y Gamma x y dusturu dogrudur
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська