Ortaq bölən və ən böyük ortaq bölən
TƏRİF. 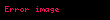

Məsələn, 60, 25, 45 ədədləri üçün 5 ədədi ortaq böləndir.
TƏRİF.Verilən 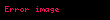
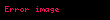
ƏBOB-u 
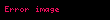


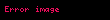
Bu təriflərdən nəticə kimi alına bilən aşağıdakı iki teoremi isbat edək.
TEOREM 1.Verilən 

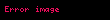

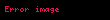
İSBATI.Aşkardır ki, 


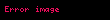






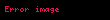
TEOREM 2. 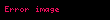



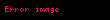
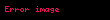
İSBATI.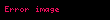
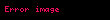
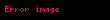


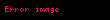







Teorem isbat olunur.
Evklid alqoritmi
Müasir riyaziyyatda ən böyük ortaq bölənin bir çox cəhətdən daha əhəmiyyətli olan aşağıdakı tərifi də var.
TƏRİF 2.


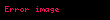

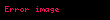

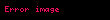
Məsələn 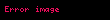










…………………………………………………
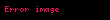
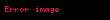
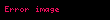
Əgər 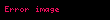




İndi aşağıdakı teoremi isbat edək.
TEOREM. 

İSBATI.Əvvəlcə göstərək ki, 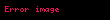


Sonuncu 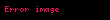
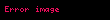
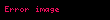
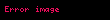
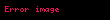


İndi 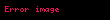
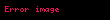



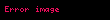
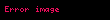
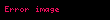
…………………………………….
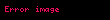
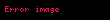
şəklində yazaq. 
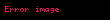
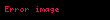
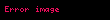
Teorem isbat olundu.
QEYD.İki 

Ədəbiyyat
- Вандер Варден Б.Л. Алгебра "Наука" 1976.
- Куликов Л.Я. Алгебра и теория чисел. М.. Высшая школа, 1979.
- Курош А.Г. Курс высшей алгебры. М., Наука. 1977
- Бухштаб А.А. Теория чисел. М., Просвещение, 1966.
- Столл Р.С. Множества.Логинка.Аксиоматические теории. Просвещение. 1968.
- Qasımov V.Ə. Cəbr və ədədlər nəzəriyyəsi. I və II his. 1998, 1999. BDU nəşriyyatı.
- M.H.Cavadov, R.Ə.Eyyubov, F.H.Əfəndiyev: Cəbr və ədədlər nəzəriyyəsi I hissə, 1988.
- M.H.Cavadov, R.Ə.Eyyubov, F.H.Əfəndiyev: Cəbr və ədədlər nəzəriyyəsi II hissə, 1989.
- M.H.Cavadov, R.Ə.Eyyubov, F.H.Əfəndiyev: Cəbr və ədədlər nəzəriyyəsi III hissə, 1992.
- Abdulkərimov L.Ş., Baxşəliyev Y.R. və b. Cəbr və ədədlər nəzəriyyəsi IV hissə, 1995.
Xarici keçidlər
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Ortaq bolen ve en boyuk ortaq bolenTERIF a1 a2 an displaystyle a 1 a 2 a n tam ededlerinin her birinin eyni zamanda bolunduyu d displaystyle d ededine bu ededlerin ortaq boleni deyilir Meselen 60 25 45 ededleri ucun 5 ededi ortaq bolendir TERIF Verilen a1 a2 an displaystyle a 1 a 2 a n ededlerinin ortaq bolenleri icerisinden en boyuyune bu ededlerin en boyuk ortaq boleni EBOB deyib onu a1 a2 an displaystyle a 1 a 2 a n kimi isare edirler EBOB u D displaystyle D ile a1 a2 an D displaystyle a 1 a 2 a n D isare edek Xususi halda iki a displaystyle a ve b displaystyle b ededleri ucun EBOB a b D displaystyle a b D Bu teriflerden netice kimi alina bilen asagidaki iki teoremi isbat edek TEOREM 1 Verilen a displaystyle a ve b displaystyle b ededlerinden a b displaystyle a b ise onda bunlarin butun ortaq bolenleri b displaystyle b ededinin bolenlerinden ibaret olur ve xususi halda a b b displaystyle a b b olur ISBATI Askardir ki a displaystyle a ve b displaystyle b nin ortaq bolenleri eyni zamanda her ikisinin o cumleden b displaystyle b nin ortaq bolenleridir Diger terefden a b displaystyle a b oldugundan b displaystyle b nin her bir boleni eyni zamanda a displaystyle a nin da boleni olmalidir Bu ise o demekdir ki a displaystyle a ve b displaystyle b nin ortaq bolenler coxlugu b displaystyle b ededinin bolenleri coxlugu ile ust uste dusur b displaystyle b ededinin en boyuk boleni ozu oldugundan a b b displaystyle a b b olur Teorem isbat olundu TEOREM 2 a bq c displaystyle a bq c munasibetinde olan a displaystyle a ve b displaystyle b ededlerinin ortaq boleni b displaystyle b ve c displaystyle c nin ortaq bolenleri ile eynidir ve xususi halda a b b c displaystyle a b b c ISBATI a bq c displaystyle a bq c ve yaxud buradan alinan a bq c displaystyle a bq c a c bq displaystyle a c bq beraberlikleri gosterir ki a displaystyle a ve b displaystyle b nin her bir ortaq boleni eyni zamanda c displaystyle c nin ortaq bolenleri olur tersine b displaystyle b ile c displaystyle c nin istenilen ortaq bolenleri a displaystyle a nin da bolenleridir ve demeli a displaystyle a ve b displaystyle b nin ortaq bolenleri olurlar Belelikle aliriq ki a displaystyle a ve b displaystyle b nin ortaq bolenleri eyni zamanda b displaystyle b ile c displaystyle c nin ortaq bolenleridir EBOB da bu ortaq bolenler icerisinde oldugu ucun a b b c displaystyle a b b c olur Teorem isbat olunur Evklid alqoritmiMuasir riyaziyyatda en boyuk ortaq bolenin bir cox cehetden daha ehemiyyetli olan asagidaki terifi de var TERIF 2 a1 a2 an displaystyle a 1 a 2 a n ededlerinin ortaq bolenleri icerisinde elesine EBOB deyirler ki o diger ortaq bolenlerin hamisina bolunsun Basqa sozle D displaystyle D ededinin verilen ededlerin EBOB u olmasi ucun iki sert odenmelidir D displaystyle D ededi a1 a2 an displaystyle a 1 a 2 a n ededlerinin ortaq bolenidir D displaystyle D ededi a1 a2 an displaystyle a 1 a 2 a n ededlerinin ixtiyari bir d displaystyle d ortaq bolenine bolunur D d displaystyle D forall d Meselen a 30 displaystyle a 30 ve c 105 displaystyle c 105 ededlerinin ortaq bolenleri 1 displaystyle 1 3 displaystyle 3 5 displaystyle 5 15 displaystyle 15 ededleridir Burada EBOB D 15 displaystyle D 15 gorunduyu kimi 15 1 displaystyle 15 1 15 3 displaystyle 15 3 15 5 displaystyle 15 5 Sonuncu 2 ci terifin ustunluyu ondadir ki EBOB anlayisini asanliqla genis riyazi obyektler coxlugu ucun umumilesdirmeye imkan verir Terif 2 den bele bir askar netice cixir ki a displaystyle a ve b displaystyle b ededlerinin butun ortaq bolenler coxlugu bunlarin EBOB nun yeni a b D displaystyle a b D ededinin bolenler coxlugu ile ust uste dusur Iki a displaystyle a ve b displaystyle b ededlerinin EBOB nu tapmaq ucun istifade edilen semereli usullardan biri antik dovrun boyuk riyaziyyatcisi Evklidin adi ile bagli olan Evklid alqorifmidir Evklid alqorifmi verilen a displaystyle a ve b displaystyle b ededlerine qaliqli bolme alqorifmini ve buradan qismet ve qaliqlara ardicil tetbiq etmekdir Bele ki verilen a displaystyle a ve b displaystyle b ededleri ucun a gt b displaystyle a gt b sertile a bq1 r1 displaystyle a bq 1 r 1 0 r1 lt b1 displaystyle 0 leq r 1 lt b 1 sonra b gt r1 displaystyle b gt r 1 ucun b r1q2 r2 displaystyle b r 1 q 2 r 2 0 r2 lt r1 displaystyle 0 leq r 2 lt r 1 0 r1 lt b1 displaystyle 0 leq r 1 lt b 1 sonra r1 gt r lt 2 displaystyle r 1 gt r lt 2 ucun r1 r2q3 r3 displaystyle r 1 r 2 q 3 r 3 0 r3 lt r2 displaystyle 0 leq r 3 lt r 2 sonra r2 gt r3 displaystyle r 2 gt r 3 ucun ve s Bu proses qaliq sifra beraber olanda qurtarir ve asagidaki beraberlikler sistemi alinir E 1 displaystyle E 1 a bq1 r1 displaystyle a bq 1 r 1 0 r1 lt b displaystyle 0 leq r 1 lt b E 2 displaystyle E 2 b r1q2 r2 displaystyle b r 1 q 2 r 2 0 r2 lt r1 displaystyle 0 leq r 2 lt r 1 E 3 displaystyle E 3 r lt 1 r2q3 r3 displaystyle r lt 1 r 2 q 3 r 3 0 r3 lt r2 displaystyle 0 leq r 3 lt r 2 E 4 displaystyle E 4 r2 r3q4 r4 displaystyle r 2 r 3 q 4 r 4 0 r4 lt r lt 3 displaystyle 0 leq r 4 lt r lt 3 E k 2 displaystyle E k 2 rk 4 rk 2qk 2 rk 2 displaystyle r k 4 r k 2 q k 2 r k 2 0 rk 2 lt rk 3 displaystyle 0 leq r k 2 lt r k 3 E k 1 displaystyle E k 1 rk 3 rk 2qk 1 rk 1 displaystyle r k 3 r k 2 q k 1 r k 1 0 rk 1 lt rk 2 displaystyle 0 leq r k 1 lt r k 2 E k displaystyle E k rk 2 rk 1qk rk displaystyle r k 2 r k 1 q k r k 0 rk lt r lt k 1 displaystyle 0 leq r k lt r lt k 1 E k 1 displaystyle E k 1 rk 1 rk lt qk 1 0 displaystyle r k 1 r k lt q k 1 0 E displaystyle E beraberliklerini Evklid beraberlikler sistemi adlandirirlar Eger b gt a displaystyle b gt a olardisa onda b displaystyle b ni a displaystyle a ya bolmekle baslayib E displaystyle E beraberliklerinde b displaystyle b ile a displaystyle a nin yerini deyiserdik Indi asagidaki teoremi isbat edek TEOREM a displaystyle a ve b displaystyle b edelerinin EBOB u E displaystyle E beraberlikler sistemindeki sonuncu 0 displaystyle 0 dan ferqli qaliqdir yeni D rk displaystyle D r k ISBATI Evvelce gosterek ki rk displaystyle r k ededi a displaystyle a ve b displaystyle b nin ortaq bolenidir Sonuncu E k 1 displaystyle E k 1 beraberliyinden gorunur ki rk 1 rk displaystyle r k 1 r k Bunu nezere alib E k displaystyle E k beraberliyine diqqet yetirsek aydin olur ki rk 2 rk displaystyle r k 2 r k cunki rk rk displaystyle r k r k ve rk 1 rk displaystyle r k 1 r k Bunu nezere alib E k 1 displaystyle E k 1 tapiriq ki rk 3 rk displaystyle r k 3 r k ve s Bu muhakimeni yuxariya dogru davam etdirmekle E 2 displaystyle E 2 den b rk displaystyle b r k E 1 displaystyle E 1 den ise a rk displaystyle a r k tapiriq Demeli rk displaystyle r k ededi a displaystyle a ve b displaystyle b nin ortaq bolenidir Indi rk displaystyle r k nin EBOB olmasi ucun 2 ci terife gore gostermeliyik ki rk displaystyle r k ededi a displaystyle a ve b displaystyle b nin ixtiyari bir d displaystyle d ortaq bolenine bolunur E displaystyle E beraberliklerini E 1 displaystyle E 1 prime a bq1 r1 displaystyle a bq 1 r 1 E 2 displaystyle E 2 prime b r1q2 r2 displaystyle b r 1 q 2 r 2 E 3 displaystyle E 3 prime r1 r2q3 r3 displaystyle r 1 r 2 q 3 r 3 E k 1 displaystyle E k 1 prime rk 3 rk 2qk 1 rk 1 displaystyle r k 3 r k 2 q k 1 r k 1 E k displaystyle E k prime rk 2 rk 1q lt k rk displaystyle r k 2 r k 1 q lt k r k E k 1 displaystyle E k 1 prime rk 1 rkqk 1 0 displaystyle r k 1 r k q k 1 0 seklinde yazaq d displaystyle d ixtiyari ortaq bolen oldugundan a d displaystyle a d ve b d displaystyle b d onda E 1 displaystyle E 1 prime den aydin olur ki r1 d displaystyle r 1 d E 2 displaystyle E 2 prime den r2 d displaystyle r 2 d E 3 displaystyle E 3 prime den r3 d displaystyle r 3 d ve s nehayet E k displaystyle E k prime den rk d displaystyle r k d oldugunu tapiriq Ona gore de a b rk D displaystyle a b r k D Teorem isbat olundu QEYD Iki a displaystyle a ve b displaystyle b ededleri b 0 displaystyle b neq 0 ucun hemise qaliqli bolme alqorifmi oldugundan en boyuk ortaq bolenin varligi da askar olur EdebiyyatVander Varden B L Algebra Nauka 1976 Kulikov L Ya Algebra i teoriya chisel M Vysshaya shkola 1979 Kurosh A G Kurs vysshej algebry M Nauka 1977 Buhshtab A A Teoriya chisel M Prosveshenie 1966 Stoll R S Mnozhestva Loginka Aksiomaticheskie teorii Prosveshenie 1968 Qasimov V E Cebr ve ededler nezeriyyesi I ve II his 1998 1999 BDU nesriyyati M H Cavadov R E Eyyubov F H Efendiyev Cebr ve ededler nezeriyyesi I hisse 1988 M H Cavadov R E Eyyubov F H Efendiyev Cebr ve ededler nezeriyyesi II hisse 1989 M H Cavadov R E Eyyubov F H Efendiyev Cebr ve ededler nezeriyyesi III hisse 1992 Abdulkerimov L S Baxseliyev Y R ve b Cebr ve ededler nezeriyyesi IV hisse 1995 Xarici kecidlerhttp eqworld ipmnet ru ru library mathematics numtheory htm http adpu edu az gen html azl fakulte Riyaziyyat fakultesi kafedra Cebr ve hendese ftp 7 htm 2016 10 12 at the Wayback Machine
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State