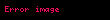Loqarifm - b ədədini almaq üçün a əsasını yüksəltmək lazım gələn qüvvət üstünə b ədədinin a əsasına görə loqarifmi deyilir: . "Loqarifm" terminini elmə ilk dəfə şotlandiya alimi Con Nepyer (1550-1617) gətirmişdir.

Loqarifmik eyniliklər
Aşağıdakı cədvəlin 1-ci tərəfində düstur, 2-ci tərəfində isə bu düsturlara aid misallar verilmişdir:
| Düstur | Misal | |
|---|---|---|
| Vurma | 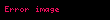 |  |
| Bölmə | 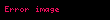 |  |
| Yüksəltmə |  | 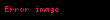 |
| Kökaltı ifadə | 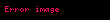 |  |
Xarici keçidlər
- Colin Byfleet, Educational video on logarithms, İstifadə tarixi: 12/10/2010
- Edward Wright, , 2007-06-27 tarixində orijinalından arxivləşdirilib, İstifadə tarixi: 12/10/2010
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Loqarifm b ededini almaq ucun a esasini yukseltmek lazim gelen quvvet ustune b ededinin a esasina gore loqarifmi deyilir loga b displaystyle log a b Loqarifm terminini elme ilk defe sotlandiya alimi Con Nepyer 1550 1617 getirmisdir Loqarifmik funksiyasinin qrafikiLoqarifmik eyniliklerAsagidaki cedvelin 1 ci terefinde dustur 2 ci terefinde ise bu dusturlara aid misallar verilmisdir Dustur MisalVurma logb xy logb x logb y displaystyle log b xy log b x log b y log3 243 log3 9 27 log3 9 log3 27 2 3 5 displaystyle log 3 243 log 3 9 cdot 27 log 3 9 log 3 27 2 3 5 Bolme logb xy logb x logb y displaystyle log b left frac x y right log b x log b y log2 16 log2 644 log2 64 log2 4 6 2 4 displaystyle log 2 16 log 2 left frac 64 4 right log 2 64 log 2 4 6 2 4 Yukseltme logb xp plogb x displaystyle log b x p p log b x log2 64 log2 26 6log2 2 6 displaystyle log 2 64 log 2 2 6 6 log 2 2 6 Kokalti ifade logb xp logb x p displaystyle log b sqrt p x frac log b x p log10 1000 12log10 1000 32 1 5 displaystyle log 10 sqrt 1000 frac 1 2 log 10 1000 frac 3 2 1 5 Xarici kecidlerColin Byfleet Educational video on logarithms Istifade tarixi 12 10 2010 Edward Wright 2007 06 27 tarixinde orijinalindan arxivlesdirilib Istifade tarixi 12 10 2010
 Azərbaycanca
Azərbaycanca සිංහල
සිංහල Türkçe
Türkçe