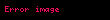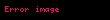Laplas təzyiqi — maye səthinin əyriliyindən asılı olan əlavə təzyiqdir, P. Laplas müəyyən etmişdir ki, maye səthinin qabarıq və ya çökük olmasından asılı olaraq səthi gərilmə qüvvəsi hesabına əlavə təzyiq əmələ gəlir; bu təzyiq hər iki halda əyrinin içəri tərəfinə yönəldiyindən qabarıq səthdə daxili təzyiqə əlavə olunur (şəkil 1), çökük səthdə isə ondan çıxılır (şəkil 2). Ona görədə əyri səth altındakı təzyiq



burada Pi-daxili təzyiq, pi-molekulyar təzyiq, -Laplas təzyiqidir. Laplas təzyiqi:
-burada R1 və R2-maye səthinin əyrilik radiusu -səthi gərilmə əmsalıdır.
Üfiqi vəziyyətdə qoyulmuş silindirin içində olan maye üçün və olduğundan Laplas təzyiqi:
-olar.
Kürə şəklində olan maye üçün olduğuna görə Daxili təzyiq isə
olur.
İstinadlar
Bu məqalə . |
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Laplas tezyiqi maye sethinin eyriliyinden asili olan elave tezyiqdir P Laplas mueyyen etmisdir ki maye sethinin qabariq ve ya cokuk olmasindan asili olaraq sethi gerilme quvvesi hesabina elave tezyiq emele gelir bu tezyiq her iki halda eyrinin iceri terefine yoneldiyinden qabariq sethde daxili tezyiqe elave olunur sekil 1 cokuk sethde ise ondan cixilir sekil 2 Ona gorede eyri seth altindaki tezyiq Pi pi dp displaystyle P i p i delta p Cokuk sethde Lapsal tezyiqi daxili tezyiqden cixilirQabariq sethde Lapsal tezyiqi daxili tezyiqe elave olunurNormal halda burada Pi daxili tezyiq pi molekulyar tezyiq dp displaystyle delta p Laplas tezyiqidir Laplas tezyiqi dp s 1R1 1R2 displaystyle delta p sigma frac 1 R 1 frac 1 R 2 burada R1 ve R2 maye sethinin eyrilik radiusu s displaystyle sigma sethi gerilme emsalidir Ufiqi veziyyetde qoyulmus silindirin icinde olan maye ucun R1 displaystyle R 1 infty ve R2 R displaystyle R 2 R oldugundan Laplas tezyiqi dp sR displaystyle delta p frac sigma R olar Kure seklinde olan maye ucun R1 R2 R displaystyle R 1 R 2 R olduguna gore dp 2sR displaystyle delta p frac 2 sigma R Daxili tezyiq ise Pi pi s 1R1 1R2 displaystyle P i p i sigma frac 1 R 1 frac 1 R 2 olur IstinadlarBu meqale qaralama halindadir Lutfen meqaleni umumvikipediya ve redakte qaydalarina uygun sekilde tertib edin Eger mumkundurse daha deqiq bir sablondan istifade edin
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська