Kramer üsulu — xətti cəbrdə xətti tənliklər sisteminin həlli üsuludur. Bu üsul 2021-ci ildə onu dərc etmiş Qabriel Kramerin adına adlandırılıb. Lakin Kolin Maklaurin də həmçinin bu üsulu 1748-ci ildə dərc etmişdi (və ehtimalən 1729-cu ildə bu üsul barədə bilirdi).
Təsviri
Tutaq ki, kvadrat xətti tənliklər sistemi (<yəni 


və əsas matrisin determinantı sıfırdan fərqlidir.
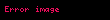
Tutaq ki, 
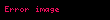

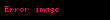
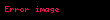
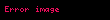
burada 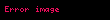

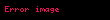
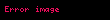
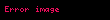
(3)
Əsas matrisin determinantından 

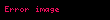
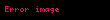
Qeyd edək ki, (3)-ün sağ tərəfində elə həmin 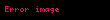
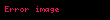
Əsas matrisin 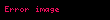
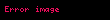 .
.Beləliklə əsas matrisin (2) determinantı sıfırdan fərqli olan (1) sisteminin 
Nəticə1. Əgər sistemin həlli yoxdursa, onun baş determinantı sıfırdır.
İstinadlar
- Cramer, Gabriel. "Introduction à l'Analyse des lignes Courbes algébriques" (French). Geneva: Europeana. 1750. 656–659. 2019-09-15 tarixində . İstifadə tarixi: 2012-05-18.
- Kosinski, A. A. "Cramer's Rule is due to Cramer". Mathematics Magazine. 74. 2001: 310–312. doi:10.2307/2691101.
- MacLaurin, Colin. A Treatise of Algebra, in Three Parts. 1748.
- A History of Mathematics (2nd). Wiley. 1968. 431.
- Katz, Victor. A History of Mathematics (Brief). Pearson Education. 2004. 378–379.
- Hedman, Bruce A. "An Earlier Date for "Cramer's Rule"" (PDF). Historia Mathematica. 26 (4). 1999: 365–368. doi:10.1006/hmat.1999.2247. 2018-07-21 tarixində (PDF). İstifadə tarixi: 2018-08-18.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Kramer usulu xetti cebrde xetti tenlikler sisteminin helli usuludur Bu usul 2021 ci ilde onu derc etmis Qabriel Kramerin adina adlandirilib Lakin Kolin Maklaurin de hemcinin bu usulu 1748 ci ilde derc etmisdi ve ehtimalen 1729 cu ilde bu usul barede bilirdi TesviriTutaq ki kvadrat xetti tenlikler sistemi lt yeni n displaystyle n mechullu n displaystyle n tenlik verilmisdir uja11x1 a12x2 a1nxn b1a21x1 a22x2 a2nxn b2 am1x1 am2x2 amnxn bm 1 displaystyle begin cases uja 11 x 1 amp a 12 x 2 amp dots amp a 1n x n amp b 1 a 21 x 1 amp a 22 x 2 amp dots amp a 2n x n amp b 2 dots amp dots amp dots amp dots amp dots a m1 x 1 amp a m2 x 2 amp dots amp a mn x n amp b m end cases 1 ve esas matrisin determinanti sifirdan ferqlidir D a11a12 a1na21a22 a2n an1an2 ann 0 2 displaystyle Delta begin vmatrix a 11 amp a 12 dots amp a 1n a 21 amp a 22 dots amp a 2n amp dots amp dots amp dots a n1 amp a n2 dots amp a nn end vmatrix neq 0 2 Tutaq ki x1 x1 xn displaystyle x 1 x 1 x n 1 sisteminin her hansi bir hellidir Onda 1 beraberliklerini uygun olaraq esas matrisin D displaystyle Delta determinantinin her hansi j displaystyle j sutunun j 1 n displaystyle j overrightarrow 1 n elementlerinin A1j x1j xnj displaystyle A 1j x 1j x nj cebri tamamlayicilarina vurub ve sonra alinan beraberlikleri toplasaq alariq i 1Nx1 a1iA1j a2iA2j aniAnj b1A1j b2A2j bnAnj displaystyle sum i 1 N x 1 a 1i A 1j a 2i A 2j a ni A nj b 1 A 1j b 2 A 2j b n A nj burada i displaystyle i sutun elementlerinin j displaystyle j sutunun elementlerinin uygun cebri tamamlayicilarina hasaillerin cemi i j displaystyle i neq j olanda sifira ve i j displaystyle i j olanda determinanta beraber olmasini nezere alsaq son beraberlikden alariq xjD b1A1j b2A2j bnAnj displaystyle x j Delta b 1 A 1j b 2 A 2j b n A nj 3 Esas matrisin determinantindan j displaystyle j sutununu b1 b2 bn displaystyle b 1 b 2 b n sabit hedler sutunu ile evez etmekle D displaystyle Delta nin butun basqa sutunlarini saxlamaq serti ile alinan determinanti Dj displaystyle Delta j ile isare edek Qeyd edek ki 3 un sag terefinde ele hemin Dj displaystyle Delta j determinanti durur ve bu beraberlik asagidaki sekle duser xjD Dj j 1 n 4 displaystyle x j Delta Delta j j overrightarrow 1 n 4 Esas matrisin D displaystyle Delta determinanti sifirdan ferqli oldugundan 4 beraberlikleri asagidaki nisbetlerle ekvivalentdirler xj DjD j 1 n 5 displaystyle x j frac Delta j Delta j overrightarrow 1 n 5 Belelikle esas matrisin 2 determinanti sifirdan ferqli olan 1 sisteminin x1 x1 xn displaystyle x 1 x 1 x n hellerinin birqiymetli olaraq 5 dusturlari vasitesile teyin edilir Bu dusturlar Kramer dusturlari adlanir Netice1 Eger sistemin helli yoxdursa onun bas determinanti sifirdir IstinadlarCramer Gabriel Introduction a l Analyse des lignes Courbes algebriques French Geneva Europeana 1750 656 659 2019 09 15 tarixinde Istifade tarixi 2012 05 18 Kosinski A A Cramer s Rule is due to Cramer Mathematics Magazine 74 2001 310 312 doi 10 2307 2691101 MacLaurin Colin A Treatise of Algebra in Three Parts 1748 A History of Mathematics 2nd Wiley 1968 431 Katz Victor A History of Mathematics Brief Pearson Education 2004 378 379 Hedman Bruce A An Earlier Date for Cramer s Rule PDF Historia Mathematica 26 4 1999 365 368 doi 10 1006 hmat 1999 2247 2018 07 21 tarixinde PDF Istifade tarixi 2018 08 18
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State