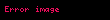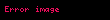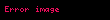Huk qanunu — cismin deformasiyası zamanı yaranan elastiklik qüvvəsi, bu deformasiyanın ölçüsü ilə düz mütənasibdir. Huk qanunu 1660-cl ildə ingilis alimi Robert Huk tərəfindən kəşf olunmuşdur. F= -kx
Huk qanunu ancaq kiçik deformasiyalarda doğrudur mütənasiblik həddini aşdıqda, gərginliklə deformasiya arasındakı asılılıq qeyri xətti olur.
Nazik çubuqlar üçün Huk qanunu
Nazik çubuğun dartılmasında Hüq qanunu aşağıdakı kimi yazılır:
Burada 

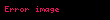
Elastikiyyət əmsalı materialın xassəsindən və ölçülərindən asılıdır. Aşkar şəkildə çubuğun ölçülərini istifadə edərək elastikiyyət əmsalını aşağıdakı kimi yazmaq olar. (kəsiyinin en sahəsi 


en kəsiyindəki normal gərginlik
Bu forma materialın hər kiçik hissəsində doğrudur.
Ümumiləşdirilmiş Huk qanunu
Ümumi halda gərginlik deformasiya üç ölçükü fəzada 2 ranqlı tenzorla istifadə olunur. (9 komponentə malikdir.) Onları əlaqələndirən tenzoru 4 ranqlı tenzor olmaqla 

burada 


gərginlik və deformasiya tenzorlarının simmetrik olması şərtindən istifadə edərək Hük qanununu aşağıdakı kimi hallarda yazmaq olar.
Xətti elastik cisim üçün:
burada 


İstinadlar
Həmçinin baxın
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Huk qanunu cismin deformasiyasi zamani yaranan elastiklik quvvesi bu deformasiyanin olcusu ile duz mutenasibdir Huk qanunu 1660 cl ilde ingilis alimi Robert Huk terefinden kesf olunmusdur F kx Huk qanunu ancaq kicik deformasiyalarda dogrudur mutenasiblik heddini asdiqda gerginlikle deformasiya arasindaki asililiq qeyri xetti olur Nazik cubuqlar ucun Huk qanunuNazik cubugun dartilmasinda Huq qanunu asagidaki kimi yazilir F kDl displaystyle F k Delta l Burada F displaystyle F quvve Dl displaystyle Delta l mutleq uzanma ya a k displaystyle k Elastikiyyet emsali materialin xassesinden ve olculerinden asilidir Askar sekilde cubugun olculerini istifade ederek elastikiyyet emsalini asagidaki kimi yazmaq olar kesiyinin en sahesi S displaystyle S ve uzunluq L displaystyle L k ESL displaystyle k frac ES L E displaystyle E ve materialin mexaniki xarakterikdir e DlL displaystyle varepsilon frac Delta l L en kesiyindeki normal gerginlik s FS displaystyle sigma frac F S s Ee displaystyle sigma E varepsilon Bu forma materialin her kicik hissesinde dogrudur Dl FLES displaystyle Delta l frac FL ES Umumilesdirilmis Huk qanunuUmumi halda gerginlik deformasiya uc olcuku fezada 2 ranqli tenzorla istifade olunur 9 komponente malikdir Onlari elaqelendiren tenzoru 4 ranqli tenzor olmaqla Cijkl displaystyle C ijkl 81 sabit teskil edir Tenzor Cijkl displaystyle C ijkl simmetrik oldugu halda getginlik ve deformasiya tenzorunda yalniz 21 sabitden asili olurlar Bu zaman Huk qanununu asagidaki kimi yazmaq olar sij klCijkl ekl displaystyle sigma ij sum kl C ijkl cdot varepsilon kl burada sij displaystyle sigma ij ekl displaystyle varepsilon kl Izatrop materialin tenzoru Cijkl displaystyle C ijkl gerginlik ve deformasiya tenzorlarinin simmetrik olmasi sertinden istifade ederek Huk qanununu asagidaki kimi hallarda yazmaq olar Xetti elastik cisim ucun ex sxE mEsy mEsz displaystyle varepsilon x frac sigma x E frac mu E sigma y frac mu E sigma z ey syE mEsx mEsz displaystyle varepsilon y frac sigma y E frac mu E sigma x frac mu E sigma z ez szE mEsx mEsy displaystyle varepsilon z frac sigma z E frac mu E sigma x frac mu E sigma y gxy txyG displaystyle gamma xy frac tau xy G gyz tyzG displaystyle gamma yz frac tau yz G gxz txzG displaystyle gamma xz frac tau xz G burada E displaystyle E m displaystyle mu G E2 1 m displaystyle G frac E 2 1 mu IstinadlarHemcinin baxin
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans