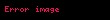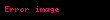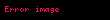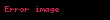şəklində tənliyə Rikkati tənliyi deyilir. Rikkati tənliyi olduqda xətti, olduqda isə çevrilir. Rikkati tənliyinin hər hansı xüsusi həlli məlum olduqda əvəzləməsi vasitəsilə Bernulli tənliyinə gətirlir. Ümumi halda, Rikkati tənliyi kvadraturaya gətirilə bilmir, yəni həll etmək olmur.
Tarixi
Xüsusi halda:
haradakı 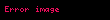




Xassələri
olduqda dəyişənlərinə ayrılan,
olduqda bircins,
olduqda ümumiləşmiş bircns tənliyə çevrilir.
Nümunə.
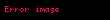
Həlli:
tənliyin həlli olduğunu bilavasitə yoxlamaq olar. Onda
əvəzləməsini aparmaqla alırıq:

Alınan tənliyi həll etsək, 
- Deməli,
Rikkati tənliyinin ümumi həlli olur.
- Deməli,
Ədəbiyyat
- Q.T. Əhmədov, K.Q. Həsəov, M.H. Yaqubov, Adi diferensial tənliklər kursu, Bakı, Maarif, 1978.
- И.Г.Петровский, Лекции по теории обыкновенных дифференциальных уравнений, М., Наука, 1984.
- Л.С.Понтрягин, Обыкновеные дифференциальные уравнения, М., Наука, 1982.
- В.В.Степанов, Курс дифференциальных уравнений, М., 1959.
- А.Ф.Филиппов, Сборник задач по дифференциальным уравнениям, М., 2004.
- X.M. Quliyev, K.Q. Həsəov, Difernsial tənliklər, Məsələ və misallar tənliyi, Bakı, Çaşıoğlu, 2001.
- M.H. Yaqubov, Y.T. Mehrəliyev, Birtərtibli adi difernsial tənliklər, BDU, Bakı, 1999.
- Л.Э.Эльсгольц, Дифференциальные уравнения и вариационные исчисление, Москва, 1969.
- Н.М.Матвеев, Методы интегрирования обыкновеных дифференциальных уравнений, Минск, Выщэйщая школа, 1974.
- А.Н.Тихонов, А.Б.Васильева, А.Г.Свешников, Дифференциальные уравнения, Москва, Наука, 1985.
İstinadlar
- Riccati J. F. Animadversationes in aequationes differentiales secundi gradus. Acta Eruditorum Quae Lipside Publicantur, 1724. Supplementa 8.
- Cantor M. Vorlesungen über Geschichte der Mathematik (V. 4). Leipzig, 1901.[ölü keçid]
- Grugnetti L. Sur Carteggio Jacopo Riccati — Nicola 2 Bernulli. J. Riccati e la Cultura della Marca nel Settecento Europeo. Firence, 1992.
Xarici keçidlər
- Wolfram Math. World: Riccati Differential Equation
- Eq. World: General Riccati equation
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
y a x y b x y2 c x 0 displaystyle y prime a x y b x y 2 c x 0 displaystyle seklinde tenliye Rikkati tenliyi deyilir Rikkati tenliyi b x 0 displaystyle b x 0 olduqda xetti c x 0 displaystyle c x 0 olduqda ise cevrilir Rikkati tenliyinin her hansi y1 x displaystyle y 1 x xususi helli melum olduqda y x y1 x z x displaystyle y x y 1 x z x evezlemesi vasitesile Bernulli tenliyine getirlir Umumi halda Rikkati tenliyi kvadraturaya getirile bilmir yeni hell etmek olmur TarixiXususi halda bdxdt x2 ata displaystyle b frac dx dt x 2 at alpha quad dd haradaki a a b 0 displaystyle alpha a b neq 0 sabiti ilk defe italyan riyaziyyatcisi tedqiq etmisdir Yakopo Francesko Rikkati ve ailelerini Bernulli a 4n 1 2n n N displaystyle alpha 4n 1 2n n in mathbb N ili a 2 displaystyle alpha 2 Jozef Liuvill 1841 isbat etmisdir displaystyle sekilde umumi Rikkati tenliyi displaystyle ise xususi Rikkati tenliyi adlanir Xasseleriy m x Ay By2 C 0 displaystyle y prime m x Ay By 2 C 0 olduqda deyisenlerine ayrilan y Ayx B yx 2 C 0 displaystyle y prime A frac y x B left frac y x right 2 C 0 olduqda bircins y Ayx B y 2 Cx2 0 displaystyle y prime A frac y x B y 2 frac C x 2 0 olduqda umumilesmis bircns tenliye cevrilir Numune y 2yex y2 e2x ex displaystyle y prime 2ye x y 2 e 2x e x Rikkati tenliyini hell edin Helli y1 x ex displaystyle y 1 x e x tenliyin helli oldugunu bilavasite yoxlamaq olar Onda y x z ex displaystyle y x z e x evezlemesini aparmaqla aliriq dd z ex 2 z ex ex z ex 2 e2x ex z z2 0 displaystyle z prime e x 2 z e x e x z e x 2 e 2x e x z prime z 2 0 Alinan tenliyi hell etsek z 1x C displaystyle z frac 1 x C Demeli y ex 1x C displaystyle y e x frac 1 x C Rikkati tenliyinin umumi helli olur dd EdebiyyatQ T Ehmedov K Q Heseov M H Yaqubov Adi diferensial tenlikler kursu Baki Maarif 1978 I G Petrovskij Lekcii po teorii obyknovennyh differencialnyh uravnenij M Nauka 1984 L S Pontryagin Obyknovenye differencialnye uravneniya M Nauka 1982 V V Stepanov Kurs differencialnyh uravnenij M 1959 A F Filippov Sbornik zadach po differencialnym uravneniyam M 2004 X M Quliyev K Q Heseov Difernsial tenlikler Mesele ve misallar tenliyi Baki Casioglu 2001 M H Yaqubov Y T Mehreliyev Birtertibli adi difernsial tenlikler BDU Baki 1999 L E Elsgolc Differencialnye uravneniya i variacionnye ischislenie Moskva 1969 N M Matveev Metody integrirovaniya obyknovenyh differencialnyh uravnenij Minsk Vyshejshaya shkola 1974 A N Tihonov A B Vasileva A G Sveshnikov Differencialnye uravneniya Moskva Nauka 1985 IstinadlarRiccati J F Animadversationes in aequationes differentiales secundi gradus Acta Eruditorum Quae Lipside Publicantur 1724 Supplementa 8 Cantor M Vorlesungen uber Geschichte der Mathematik V 4 Leipzig 1901 olu kecid Grugnetti L Sur Carteggio Jacopo Riccati Nicola 2 Bernulli J Riccati e la Cultura della Marca nel Settecento Europeo Firence 1992 Xarici kecidlerWolfram Math World Riccati Differential Equation Eq World General Riccati equation
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State