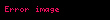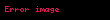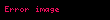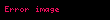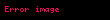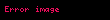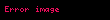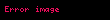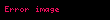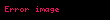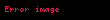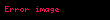Qauss funksiyalarının inteqrallarının siyahısı

Bu ifadələrdə,

${\displaystyle \phi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}}$

standart normal ehtimal sıxlığı funksiyası,

${\displaystyle \Phi (x)=\int _{-\infty }^{x}\phi (t)\,dt={\frac {1}{2}}\left(1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right)}$

müvafiq kumulativ paylama funksiyası (erf xəta funksiyasdır) və

${\displaystyle T(h,a)=\phi (h)\int _{0}^{a}{\frac {\phi (hx)}{1+x^{2}}}\,dx}$

Ouen funksiyasıdır.

Qeyri-müəyyən inteqrallar

${\displaystyle \int \phi (x)\,dx=\Phi (x)+C}$

${\displaystyle \int x\phi (x)\,dx=-\phi (x)+C}$

${\displaystyle \int x^{2}\phi (x)\,dx=\Phi (x)-x\phi (x)+C}$

${\displaystyle \int x^{2k+1}\phi (x)\,dx=-\phi (x)\sum _{j=0}^{k}{\frac {(2k)!!}{(2j)!!}}x^{2j}+C}$

${\displaystyle \int x^{2k+2}\phi (x)\,dx=-\phi (x)\sum _{j=0}^{k}{\frac {(2k+1)!!}{(2j+1)!!}}x^{2j+1}+(2k+1)!!\,\Phi (x)+C}$

Bu inteqrallarda n!! ikiqat faktorialdır: n cüt ədəd olduqda bu faktorialın qiyməti 2-dən n ə qədər olan bütün cüt ədədlərin hasilinə, n tək olduqda isə 1-dən n ə qədər olan bütün tək ədədlərin hasilinə bərabərdir. Əlavə olaraq qəbul edilir ki, 0 !! = (−1) !! = 1.

${\displaystyle \int \phi (x)^{2}\,dx={\frac {1}{2{\sqrt {\pi }}}}\Phi \left(x{\sqrt {2}}\right)+C}$

${\displaystyle \int \phi (x)\phi (a+bx)\,dx={\frac {1}{t}}\phi \left({\frac {a}{t}}\right)\Phi \left(tx+{\frac {ab}{t}}\right)+C,\qquad t={\sqrt {1+b^{2}}}}$

${\displaystyle \int x\phi (a+bx)\,dx=-{\frac {1}{b^{2}}}\left(\phi (a+bx)+a\Phi (a+bx)\right)+C}$

${\displaystyle \int x^{2}\phi (a+bx)\,dx={\frac {1}{b^{3}}}\left((a^{2}+1)\Phi (a+bx)+(a-bx)\phi (a+bx)\right)+C}$

${\displaystyle \int \phi (a+bx)^{n}\,dx={\frac {1}{b{\sqrt {n(2\pi )^{n-1}}}}}\Phi \left({\sqrt {n}}(a+bx)\right)+C}$

${\displaystyle \int \Phi (a+bx)\,dx={\frac {1}{b}}\left((a+bx)\Phi (a+bx)+\phi (a+bx)\right)+C}$

${\displaystyle \int x\Phi (a+bx)\,dx={\frac {1}{2b^{2}}}\left((b^{2}x^{2}-a^{2}-1)\Phi (a+bx)+(bx-a)\phi (a+bx)\right)+C}$

${\displaystyle \int x^{2}\Phi (a+bx)\,dx={\frac {1}{3b^{3}}}\left((b^{3}x^{3}+a^{3}+3a)\Phi (a+bx)+(b^{2}x^{2}-abx+a^{2}+2)\phi (a+bx)\right)+C}$

${\displaystyle \int x^{n}\Phi (x)\,dx={\frac {1}{n+1}}\left(\left(x^{n+1}-nx^{n-1}\right)\Phi (x)+x^{n}\phi (x)+n(n-1)\int x^{n-2}\Phi (x)\,dx\right)+C}$

${\displaystyle \int x\phi (x)\Phi (a+bx)\,dx={\frac {b}{t}}\phi \left({\frac {a}{t}}\right)\Phi \left(xt+{\frac {ab}{t}}\right)-\phi (x)\Phi (a+bx)+C,\qquad t={\sqrt {1+b^{2}}}}$

${\displaystyle \int \Phi (x)^{2}\,dx=x\Phi (x)^{2}+2\Phi (x)\phi (x)-{\frac {1}{\sqrt {\pi }}}\Phi \left(x{\sqrt {2}}\right)+C}$

${\displaystyle \int e^{cx}\phi (bx)^{n}\,dx={\frac {e^{\frac {c^{2}}{2nb^{2}}}}{b{\sqrt {n(2\pi )^{n-1}}}}}\Phi \left({\frac {b^{2}xn-c}{b{\sqrt {n}}}}\right)+C,\qquad b\neq 0,n>0}$

Müəyyən inteqrallar

${\displaystyle \int _{-\infty }^{\infty }x^{2}\phi (x)^{n}\,dx={\frac {1}{\sqrt {n^{3}(2\pi )^{n-1}}}}}$

${\displaystyle \int _{-\infty }^{0}\phi (ax)\Phi (bx)dx={\frac {1}{2\pi |a|}}\left({\frac {\pi }{2}}-\arctan \left({\frac {b}{|a|}}\right)\right)}$

${\displaystyle \int _{0}^{\infty }\phi (ax)\Phi (bx)\,dx={\frac {1}{2\pi |a|}}\left({\frac {\pi }{2}}+\arctan \left({\frac {b}{|a|}}\right)\right)}$

${\displaystyle \int _{0}^{\infty }x\phi (x)\Phi (bx)\,dx={\frac {1}{2{\sqrt {2\pi }}}}\left(1+{\frac {b}{\sqrt {1+b^{2}}}}\right)}$

${\displaystyle \int _{0}^{\infty }x^{2}\phi (x)\Phi (bx)\,dx={\frac {1}{4}}+{\frac {1}{2\pi }}\left({\frac {b}{1+b^{2}}}+\arctan(b)\right)}$

${\displaystyle \int _{0}^{\infty }x\phi (x)^{2}\Phi (x)\,dx={\frac {1}{4\pi {\sqrt {3}}}}}$

${\displaystyle \int _{0}^{\infty }\Phi (bx)^{2}\phi (x)\,dx={\frac {1}{2\pi }}\left(\arctan(b)+\arctan {\sqrt {1+2b^{2}}}\right)}$

${\displaystyle \int _{-\infty }^{\infty }\Phi (a+bx)^{2}\phi (x)\,dx=\Phi \left({\frac {a}{\sqrt {1+b^{2}}}}\right)-2T\left({\frac {a}{\sqrt {1+b^{2}}}},{\frac {1}{\sqrt {1+2b^{2}}}}\right)}$

${\displaystyle \int _{-\infty }^{\infty }x\Phi (a+bx)^{2}\phi (x)\,dx={\frac {2b}{\sqrt {1+b^{2}}}}\phi \left({\frac {a}{t}}\right)\Phi \left({\frac {a}{{\sqrt {1+b^{2}}}{\sqrt {1+2b^{2}}}}}\right)}$

${\displaystyle \int _{-\infty }^{\infty }\Phi (bx)^{2}\phi (x)\,dx={\frac {1}{\pi }}\arctan {\sqrt {1+2b^{2}}}}$

${\displaystyle \int _{-\infty }^{\infty }x\phi (x)\Phi (bx)\,dx=\int _{-\infty }^{\infty }x\phi (x)\Phi (bx)^{2}\,dx={\frac {b}{\sqrt {2\pi (1+b^{2})}}}}$

${\displaystyle \int _{-\infty }^{\infty }\Phi (a+bx)\phi (x)\,dx=\Phi \left({\frac {a}{\sqrt {1+b^{2}}}}\right)}$

${\displaystyle \int _{-\infty }^{\infty }x\Phi (a+bx)\phi (x)\,dx={\frac {b}{t}}\phi \left({\frac {a}{t}}\right),\qquad t={\sqrt {1+b^{2}}}}$

${\displaystyle \int _{0}^{\infty }x\Phi (a+bx)\phi (x)\,dx={\frac {b}{t}}\phi \left({\frac {a}{t}}\right)\Phi \left(-{\frac {ab}{t}}\right)+{\frac {1}{\sqrt {2\pi }}}\Phi (a),\qquad t={\sqrt {1+b^{2}}}}$

${\displaystyle \int _{-\infty }^{\infty }\ln(x^{2}){\frac {1}{\sigma }}\phi \left({\frac {x}{\sigma }}\right)\,dx=\ln(\sigma ^{2})-\gamma -\ln 2\approx \ln(\sigma ^{2})-1.27036}$

İstinadlar

1. Patel, Read, (1996) lists this integral above without the minus sign, which is an error. See calculation by WolframAlpha Arxivləşdirilib 2019-11-06 at the Wayback Machine
2. Patel, Read, (1996) report this integral with error, see WolframAlpha Arxivləşdirilib 2019-11-06 at the Wayback Machine
3. Patel, Read, (1996) report this integral incorrectly by omitting x from the integrand

• Patel, Jagdish K.; Read, Campbell B. Handbook of the normal distribution (2nd). CRC Press. 1996. ISBN .

• Owen, D. "A table of normal integrals". Communications in Statistics: Simulation and Computation. B9. 1980: 389–419.