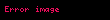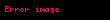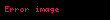Mikroiqtisadiyyatda istifadə olunan Marşal tələb funksiyası (ing. Marshallian demand function) (Alfred Marşal şərəfinə) göstərir ki, istehlakçı hər bir qiymət və var-dövlət vəziyyətində nə qədər alacaq, nəzərə alaraq ki bu qərar faydanın maksimallaşdırılmasının problemini həll edəcək. Marşal tələb funksiyası həm də Valras tələbi (Leon Valrasın şərəfinə) və ya "əvəzini verməyən tələb funksiyası" kimi tanınır, çünki Marşalın ilkin təhlili var-dövlətin effektlərini nəzərə almırdı.
Faydanın maksimallaşdırılması probleminə uyğun olaraq, p qiymətlərinə L məhsullar var. w var-dövlətinə malik olan istehlakçı və bir sıra imkanı çatan seçimlər mövcüddur:
- ,
burada, qiymətlərin daxili məhsul fəzası və məhsulların sayıdır. İstehlakçının faydalılıq düsturu aşağıdakı kimidir:
- .
İstehlakçının Marşal tələb müvafiqliyi belə təyin olunur:
- .
Əgər faydanı maksimallaşdıran seçim hər bir qiymət və var-dövlət üçün yeganədirsə, bu Marşal tələb funksiyası adlanır.
Misal
Əgər iki məhsul varsa, onda öz gəlirini həmişə hər bir məhsul üçün yarıya bölən istehlakçı Marşal tələb funksiyasına malikdir.
Həmçinin bax
İstinadlar
- Mas-Colell, Andreu; Whinston, Michael; & Green, Jerry (1995). Microeconomic Theory. Oxford: Oxford University Press.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Mikroiqtisadiyyatda istifade olunan Marsal teleb funksiyasi ing Marshallian demand function Alfred Marsal serefine gosterir ki istehlakci her bir qiymet ve var dovlet veziyyetinde ne qeder alacaq nezere alaraq ki bu qerar faydanin maksimallasdirilmasinin problemini hell edecek Marsal teleb funksiyasi hem de Valras telebi Leon Valrasin serefine ve ya evezini vermeyen teleb funksiyasi kimi taninir cunki Marsalin ilkin tehlili var dovletin effektlerini nezere almirdi Faydanin maksimallasdirilmasi problemine uygun olaraq p qiymetlerine L mehsullar var w var dovletine malik olan istehlakci ve bir sira imkani catan secimler movcuddur B p w x p x w displaystyle B p w x langle p x rangle leq w burada p x displaystyle langle p x rangle qiymetlerin daxili mehsul fezasi ve mehsullarin sayidir Istehlakcinin faydaliliq dusturu asagidaki kimidir u R L R displaystyle u textbf R L rightarrow textbf R Istehlakcinin Marsal teleb muvafiqliyi bele teyin olunur x p w argmaxx B p w u x displaystyle x p w operatorname argmax x in B p w u x Eger faydani maksimallasdiran secim her bir qiymet ve var dovlet ucun yeganedirse bu Marsal teleb funksiyasi adlanir MisalEger iki mehsul varsa onda oz gelirini hemise her bir mehsul ucun yariya bolen istehlakci Marsal teleb funksiyasina malikdir x p1 p2 w w2p1 w2p2 displaystyle x p 1 p 2 w left frac w 2p 1 frac w 2p 2 right Hemcinin baxHiks teleb funksiyasi Faydanin maksimallasdirilmasi problemiIstinadlarMas Colell Andreu Whinston Michael amp Green Jerry 1995 Microeconomic Theory Oxford Oxford University Press ISBN 0 19 507340 2
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State