Bifurkasiya nəzəriyyəsi (ing. Bifurcation theory) — bir sistemin parametrlərindəki kiçik dəyişikliklərin onun uzunmüddətli davranışını necə dəyişə biləcəyini araşdıran riyazi sahədir. Bu nəzəriyyə qeyri-xətti dinamik sistemlərdə kritik keçid nöqtələrini müəyyənləşdirmək üçün istifadə olunur və müxtəlif elmi sahələrdə, o cümlədən fizikada, biologiyada, mühəndislikdə və iqtisadiyyatda tətbiq edilir.

Bifurkasiya nəzəriyyəsi qeyri-xətti sistemlərin anlaşılmasında vacib vasitədir. Kiçik dəyişikliklərin böyük nəticələrə səbəb ola biləcəyi vəziyyətləri təhlil etmək üçün istifadə olunur. Sistemlərdə sabitlik və sabit nöqtələrin dəyişməsi, real dünyadakı dinamik proseslərin proqnozlaşdırılması və idarə olunmasında əsas rol oynayır.
Bifurkasiya növləri
- Süngərsəl (ing. Pitchfork) Bifurkasiya — parametr müəyyən bir kritik həddə çatdıqda, bir sabit nöqtə iki yeni sabit nöqtəyə ayrılır.
- İki növü var:
- Sabitlik qorunan (superkritik): Yaranan yeni sabit nöqtələr sabit olur.
- Sabitlik itən (subkritik): Yeni sabit nöqtələr sabit olmur.
- İki növü var:
- Şeytan çarxı (Hopf) Bifurkasiya — sabit nöqtənin sabitliyi dəyişir və sistemdə dövr edən həllər yaranır (limit dövrələr).
- Qəfil dəyişiklik (Səviyyəli) Bifurkasiya — parametrdə kiçik dəyişiklik, sistemdə ani və dramatik dəyişikliklərə səbəb olur.
- Qatlanan (Fold) Bifurkasiya — iki sabit nöqtə birləşir və yox olur. Bu, sistemin sabit həllərdən qeyri-sabit həllərə keçidini ifadə edir.
Riyazi ifadə
Bifurkasiya nəzəriyyəsi adətən diferensial tənliklər və ya xətti olmayan xətti tənliklər vasitəsilə təsvir edilir. Tənlik forması:
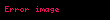
Burada:
— sistem vəziyyətini təsvir edən dəyişən.
— sistem parametri.
— dinamik funksiyanı təsvir edən tənlik.
Bifurkasiya baş verən nöqtələrdə 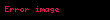
İstinadlar
- Blanchard, P.; ; Hall, G. R. Differential Equations. London: Thompson. 2006. 96–111. ISBN .
- Nonlinear Dynamics and Chaos. Addison-Wesley. 1994. səh. 262. ISBN .
- Gutzwiller, Martin C. Chaos in Classical and Quantum Mechanics. New York: Springer-Verlag. 1990. ISBN .
- Henri Poincaré. "L'Équilibre d'une masse fluide animée d'un mouvement de rotation". Acta Mathematica, vol.7, pp. 259-380, Sept 1885.
- Luo, Dingjun. Bifurcation Theory and Methods of Dynamical Systems. World Scientific. 1997. səh. 26. ISBN .
- James P. Keener, "Infinite Period Bifurcation and Global Bifurcation Branches", SIAM Journal on Applied Mathematics, Vol. 41, No. 1 (August, 1981), pp. 127–144.
Ədəbiyyat
- Guardia, M.; Martinez-Seara, M.; Teixeira, M. A. (2011). Generic bifurcations of low codimension of planar Filippov Systems. "Journal of differential equations", Febrer 2011, vol. 250, núm. 4, pp. 1967–2023. DOI:10.1016/j.jde.2010.11.016
- Wiggins, Stephen. Global bifurcations and Chaos: Analytical Methods. New York: Springer. 1988. ISBN .
- Afrajmovich, V. S.; Arnold, V. I.; və b. Bifurcation Theory and Catastrophe Theory. Springer. 1994. ISBN .
Xarici keçidlər
- Nonlinear dynamics
- Bifurcations and Two Dimensional Flows by Elmer G. Wiens
- Introduction to Bifurcation theory by John David Crawford
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Bifurkasiya nezeriyyesi ing Bifurcation theory bir sistemin parametrlerindeki kicik deyisikliklerin onun uzunmuddetli davranisini nece deyise bileceyini arasdiran riyazi sahedir Bu nezeriyye qeyri xetti dinamik sistemlerde kritik kecid noqtelerini mueyyenlesdirmek ucun istifade olunur ve muxtelif elmi sahelerde o cumleden fizikada biologiyada muhendislikde ve iqtisadiyyatda tetbiq edilir Yeher duyunlerinin bifurkasiyasini gosteren merhele portreti Bifurkasiya nezeriyyesi qeyri xetti sistemlerin anlasilmasinda vacib vasitedir Kicik deyisikliklerin boyuk neticelere sebeb ola bileceyi veziyyetleri tehlil etmek ucun istifade olunur Sistemlerde sabitlik ve sabit noqtelerin deyismesi real dunyadaki dinamik proseslerin proqnozlasdirilmasi ve idare olunmasinda esas rol oynayir Bifurkasiya novleriSungersel ing Pitchfork Bifurkasiya parametr mueyyen bir kritik hedde catdiqda bir sabit noqte iki yeni sabit noqteye ayrilir Iki novu var Sabitlik qorunan superkritik Yaranan yeni sabit noqteler sabit olur Sabitlik iten subkritik Yeni sabit noqteler sabit olmur Seytan carxi Hopf Bifurkasiya sabit noqtenin sabitliyi deyisir ve sistemde dovr eden heller yaranir limit dovreler Qefil deyisiklik Seviyyeli Bifurkasiya parametrde kicik deyisiklik sistemde ani ve dramatik deyisikliklere sebeb olur Qatlanan Fold Bifurkasiya iki sabit noqte birlesir ve yox olur Bu sistemin sabit hellerden qeyri sabit hellere kecidini ifade edir Riyazi ifadeBifurkasiya nezeriyyesi adeten diferensial tenlikler ve ya xetti olmayan xetti tenlikler vasitesile tesvir edilir Tenlik formasi dxdt f x m displaystyle frac dx dt f x mu Burada x displaystyle x sistem veziyyetini tesvir eden deyisen m displaystyle mu sistem parametri f x m displaystyle f x mu dinamik funksiyani tesvir eden tenlik Bifurkasiya bas veren noqtelerde f x m displaystyle f x mu 0 serti temin olunur ve sabitlik analizi ucun funksiyanin toremeleri istifade edilir IstinadlarBlanchard P Hall G R Differential Equations London Thompson 2006 96 111 ISBN 978 0 495 01265 8 Nonlinear Dynamics and Chaos Addison Wesley 1994 seh 262 ISBN 0 201 54344 3 Gutzwiller Martin C Chaos in Classical and Quantum Mechanics New York Springer Verlag 1990 ISBN 978 0 387 97173 5 Henri Poincare L Equilibre d une masse fluide animee d un mouvement de rotation Acta Mathematica vol 7 pp 259 380 Sept 1885 Luo Dingjun Bifurcation Theory and Methods of Dynamical Systems World Scientific 1997 seh 26 ISBN 981 02 2094 4 James P Keener Infinite Period Bifurcation and Global Bifurcation Branches SIAM Journal on Applied Mathematics Vol 41 No 1 August 1981 pp 127 144 EdebiyyatGuardia M Martinez Seara M Teixeira M A 2011 Generic bifurcations of low codimension of planar Filippov Systems Journal of differential equations Febrer 2011 vol 250 num 4 pp 1967 2023 DOI 10 1016 j jde 2010 11 016 Wiggins Stephen Global bifurcations and Chaos Analytical Methods New York Springer 1988 ISBN 978 0 387 96775 2 Afrajmovich V S Arnold V I ve b Bifurcation Theory and Catastrophe Theory Springer 1994 ISBN 978 3 540 65379 0 Xarici kecidlerNonlinear dynamics Bifurcations and Two Dimensional Flows by Elmer G Wiens Introduction to Bifurcation theory by John David Crawford
 Azərbaycanca
Azərbaycanca සිංහල
සිංහල Türkçe
Türkçe

