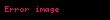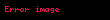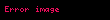0.999… (həmçinin 0.9, 0.(9) kimi yazılır) — Riyaziyyatda onluq nöqtədən sonra yazılan sonsuz sayda 9 rəqəmindən ibarət olan rasional ədəd. 0.999… ədədi 0.9, 0.99, 0.999 və s. kimi ədədlərin hamısından böyükdür. Bu ədəd 1-ə bərabər olaraq göstərilə bilər. Başqa sözlə "0.999 …" və "1" eyni ədədi təmsil edir. Bu bərabərliyin riyazi olaraq sübuta yetirilməsinin bir çox yolu var.

Cəbri isbatlar
Dövri kəsrlərdən
Hər rasional ifadə sonlu sayda rəqəm ehtiva edən onluq ədədlərlə ifadə edilə bilməz. Məsələn;
kimi.
Əgər ikinci bərabərliyin hər iki tərəfini 3-ə vursaq:
bərabərliyini alarıq.
Dörd əməliyyatdan


Hər iki tərəfi 10-a vuraq.
Hər iki tərəfdən ədədin özünü, yəni 
Sadələşdirək.
Limitdən
Ədədimizi limit dilində ifadə ədək:

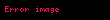
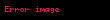
dir.
Sonsuz ardıcıllıqlardan
Teorem:


Ümumi termini 
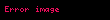

olduğunu görə bilərik.
İstinadlar
- 0.9, 0.99, 0.999 və s. kimi ifadələrdə sonuncu mərtəbədən sonra 0 rəqəmləri yazıla bilər və bu ifadənin qiymətini dəyişmir. Riyaziyyatdan məlumdur ki:
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
0 999 hemcinin 0 9 0 9 kimi yazilir Riyaziyyatda onluq noqteden sonra yazilan sonsuz sayda 9 reqeminden ibaret olan rasional eded 0 999 ededi 0 9 0 99 0 999 ve s kimi ededlerin hamisindan boyukdur Bu eded 1 e beraber olaraq gosterile biler Basqa sozle 0 999 ve 1 eyni ededi temsil edir Bu beraberliyin riyazi olaraq subuta yetirilmesinin bir cox yolu var Onluq kesrde 9 reqemi sonsuza kimi tekrarlanir Cebri isbatlarDovri kesrlerden Her rasional ifade sonlu sayda reqem ehtiva eden onluq ededlerle ifade edile bilmez Meselen 59 0 5 displaystyle frac 5 9 0 5 13 0 3 displaystyle frac 1 3 0 3 kimi Eger ikinci beraberliyin her iki terefini 3 e vursaq 33 3 0 3 displaystyle frac 3 3 3 times 0 bar 3 1 0 9 displaystyle 1 0 9 beraberliyini alariq Dord emeliyyatdan 0 9 displaystyle 0 9 ededini riyaziyyat dilinde mechul ifadelere verilen x displaystyle x ile evezleyek x 0 9 displaystyle x 0 9 Her iki terefi 10 a vuraq 10x 9 9 displaystyle 10x 9 9 Her iki terefden ededin ozunu yeni x displaystyle x i cixaq 9x 10x x 9 9 0 9 9 displaystyle 9x 10x x 9 9 0 9 9 Sadelesdirek x 1 displaystyle x 1 Limitden Ededimizi limit dilinde ifade edek 0 999 limn 0 99 9 n limn k 1n910k limn 1 110n displaystyle 0 999 ldots lim n to infty 0 underbrace 99 ldots 9 n lim n to infty sum k 1 n frac 9 10 k lim n to infty left 1 frac 1 10 n right n displaystyle n sonsuza yaxinlasarken 110n displaystyle frac 1 10 n ifadesi 0 displaystyle 0 a beraberdir Buradan alinir ki 1 limn 110n 1 displaystyle 1 lim n to infty frac 1 10 n 1 dir Sonsuz ardicilliqlardan Teorem r lt 1 displaystyle r lt 1 ve a displaystyle a sabit ededdir ve ar ar2 ar3 ar1 r displaystyle ar ar 2 ar 3 cdots frac ar 1 r dir Umumi termini r 110 displaystyle r textstyle frac 1 10 ve sabit ededi 9 displaystyle 9 olan ardicilliq 0 9 displaystyle 0 9 dur Teoremimizi ededimize tetbiq etsek 0 999 9 110 9 110 2 9 110 3 9 110 1 110 1 displaystyle 0 999 ldots 9 tfrac 1 10 9 tfrac 1 10 2 9 tfrac 1 10 3 cdots frac 9 tfrac 1 10 1 tfrac 1 10 1 oldugunu gore bilerik Istinadlar0 9 0 99 0 999 ve s kimi ifadelerde sonuncu mertebeden sonra 0 reqemleri yazila biler ve bu ifadenin qiymetini deyismir Riyaziyyatdan melumdur ki 0 9000 lt 0 9900 lt lt 0 9999 displaystyle 0 9000 lt 0 9900 lt lt 0 9999
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська