Bu məqaləni lazımdır. |
Bu məqalədəki məlumatların olması üçün əlavə mənbələrə ehtiyac var. |
1) 2; 5; 8; 11; 14; ... ,
2) – 1; 3; 7; 11; 15; ... ,
3) 3; 1; – 1; – 3; – 5; ... , ədədi ardıcıllıqlarından (1)-də ikincidən başlayaraq hər bir hədd özündən əvvəlki hədlə 3-ün cəminə, (2)-də ikincidən başlayaraq hər bir hədd özündən əvvəlki hədlə 4-ün cəminə, (3)-də ikincidən başlayaraq hər bir hədd özündən əvvəlki hədlə (– 2)-nin cəminə bərabərdir. Bu növ ədədi ardıcıllıqlar ədədi silsilə adlanır.
İkincidən başlayaraq hər bir həddi özündən əvvəlki hədlə eyni bir ədədin cəminə bərabər olan ədədi ardıcıllığa ədədi silsilə deyilir. Başqa sözlə, istənilən natural üçün
- olarsa, ardıcıllığına ədədi silsilə deyilir, burada hər hansı ədəddir.
Ədədi silsilənin bu tərifindən görünür ki, birinci dən başlayaraq hər bir həddən özündən əvvəlki həddi çıxsaq, eyni bir ədədi alınar. ədədinə ədədi silsilənin fərqi deyilir:
- bu düsturda əgər olarsa, ədədi silsilə artan ardıcıllıq, olarsa, azalan ardıcıllıq, olarsa, sabit ardıcıllıq olur.
Ədədi silsilə o zaman verilmiş hesab edilir ki, onun - birinci həddi və - silsilə fərqi verilmiş olsun. Yəni və verilsə ədədi silsiləsinin istənilən həddini
- düsturu ilə tapmaq olar. Bu düstura ədədi silsilənin n-ci həddinin düsturu deyilir.
- düsturunu şəklində yazıb, , işarə etsək, alarıq.
Ədədi silsilənin xassələri
Ədədi silsilənin 
1. Sonlu ədədi silsilədə uclardan eyni uzaqlıqda duran hədlərin cəmi kənar hədlərin cəminə bərabərdir. Yəni, 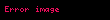
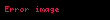

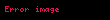
burada,
əvvəldən
-cı hədd,
isə axırdan
-cı həddir.
2. Ədədi silsilədə indekslərinin cəmi bərabər olan hədlərin cəmi bərabərdir. Yəni, 

3. 

4. Ədədi silsilədə ikincidən başlayaraq hər bir hədd özündən əvvəlki və sonrakı hədlərin ədədi ortasına bərabərdir. Yəni,
buna ədədi silsilənin xarakterik xassəsi deyilir.
5. 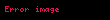
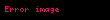

6. 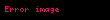
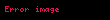


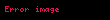

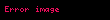
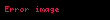

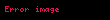
. Bu düsturda
olduğunu nəzərə alsaq daha ətraflı olan bu düsturu alarıq:
. Bu düsturların hər ikisi ədədi silsilənin ilk
həddinin cəmi düsturları adlanır.
7. Ədədi silsilənin 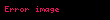

düsturu ilə hesablanır.
8. Ədədi silsilənin ilk 

düsturu ilə hesablamaq olar.
Həmçinin bax
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Bu meqaleni vikilesdirmek lazimdir Lutfen meqaleni umumvikipediya ve redakte qaydalarina uygun sekilde tertib edin Bu meqaledeki melumatlarin yoxlanilabiler olmasi ucun elave menbelere ehtiyac var Daha etrafli melumat ve ya meqaledeki problemlerle bagli muzakire aparmaq ucun diqqet yetire bilersiniz Lutfen meqaleye etibarli menbeler elave ederek bu meqaleni tekmillesdirmeye komek edin Menbesiz mezmun problemler yarada ve siline biler Problemler hell edilmemis sablonu meqaleden cixarmayin 1 2 5 8 11 14 2 1 3 7 11 15 3 3 1 1 3 5 ededi ardicilliqlarindan 1 de ikinciden baslayaraq her bir hedd ozunden evvelki hedle 3 un cemine 2 de ikinciden baslayaraq her bir hedd ozunden evvelki hedle 4 un cemine 3 de ikinciden baslayaraq her bir hedd ozunden evvelki hedle 2 nin cemine beraberdir Bu nov ededi ardicilliqlar ededi silsile adlanir Ikinciden baslayaraq her bir heddi ozunden evvelki hedle eyni bir ededin cemine beraber olan ededi ardicilliga ededi silsile deyilir Basqa sozle istenilen natural n displaystyle n ucun an 1 an d displaystyle a n 1 a n d olarsa an displaystyle a n ardicilligina ededi silsile deyilir burada d displaystyle d her hansi ededdir Ededi silsilenin bu terifinden gorunur ki birinci den baslayaraq her bir hedden ozunden evvelki heddi cixsaq eyni bir d displaystyle d ededi alinar d displaystyle d ededine ededi silsilenin ferqi deyilir an 1 an d displaystyle a n 1 a n d bu dusturda eger d gt 0 displaystyle d gt 0 olarsa ededi silsile artan ardicilliq d lt 0 displaystyle d lt 0 olarsa azalan ardicilliq d 0 displaystyle d 0 olarsa sabit ardicilliq olur Ededi silsile o zaman verilmis hesab edilir ki onun a1 displaystyle a 1 birinci heddi ve d displaystyle d silsile ferqi verilmis olsun Yeni a1 displaystyle a 1 ve d displaystyle d verilse an displaystyle a n ededi silsilesinin istenilen heddini an a1 n 1 d displaystyle a n a 1 n 1 d dusturu ile tapmaq olar Bu dustura ededi silsilenin n ci heddinin dusturu deyilir an a1 n 1 d displaystyle a n a 1 n 1 d dusturunu an nd a1 d displaystyle a n nd a 1 d seklinde yazib d k displaystyle d k a1 d b displaystyle a 1 d b isare etsek an kn b displaystyle a n kn b alariq Ededi silsilenin xasseleriEdedi silsilenin n displaystyle n ci heddinin dusturunun tetbiqi ile onun asagidaki xasseleri alinir 1 Sonlu ededi silsilede uclardan eyni uzaqliqda duran hedlerin cemi kenar hedlerin cemine beraberdir Yeni a1 displaystyle a 1 a2 displaystyle a 2 a3 displaystyle a 3 an 1 displaystyle a n 1 an displaystyle a n ededi silsilesinde bu dustur alinir ak an k 1 a1 an displaystyle a k a n k 1 a 1 a n burada ak displaystyle a k evvelden k displaystyle k ci hedd an k 1 displaystyle a n k 1 ise axirdan k displaystyle k ci heddir 2 Ededi silsilede indekslerinin cemi beraber olan hedlerin cemi beraberdir Yeni n m k l displaystyle n m k l olarsa an am ak al displaystyle a n a m a k a l olar 3 n k l2 displaystyle n frac k l 2 olduqda ededi silsilede an ak al2 displaystyle a n frac a k a l 2 olur 4 Ededi silsilede ikinciden baslayaraq her bir hedd ozunden evvelki ve sonraki hedlerin ededi ortasina beraberdir Yeni an an 1 an 12 n gt 1 displaystyle a n frac a n 1 a n 1 2 n gt 1 buna ededi silsilenin xarakterik xassesi deyilir 5 an displaystyle a n ededi silsilesinde n gt m displaystyle n gt m olduqda an am n m d displaystyle a n a m n m d beraberliyi dogrudur 6 n gt m displaystyle n gt m olduqda an displaystyle a n ededi silsilesi ucun d an amn m displaystyle d frac a n a m n m beraberliyi dogrudur d displaystyle d ededi silsilenin ferqidir an displaystyle a n ededi silsilesinin ilk n displaystyle n heddinin cemi yeni a1 displaystyle a 1 a2 displaystyle a 2 a3 displaystyle a 3 an displaystyle a n cemi bu dusturla hesablanir Sn a1 an2 n displaystyle S n frac a 1 a n 2 n Bu dusturda an a1 n 1 d displaystyle a n a 1 n 1 d oldugunu nezere alsaq daha etrafli olan bu dusturu alariq Sn 2a1 n 1 d2 n displaystyle S n frac 2a 1 n 1 d 2 n Bu dusturlarin her ikisi ededi silsilenin ilk n displaystyle n heddinin cemi dusturlari adlanir 7 Ededi silsilenin k displaystyle k ci heddi melum olduqda onun ilk 2k 1 displaystyle 2k 1 sayda heddinin cemi S2k 1 2k 1 ak displaystyle S 2k 1 2k 1 a k dusturu ile hesablanir 8 Ededi silsilenin ilk n displaystyle n heddinin cemi Sn displaystyle S n in ifadesi melum olduqda onun her hansi k displaystyle k nomreli heddini ak Sk Sk 1 displaystyle a k S k S k 1 dusturu ile hesablamaq olar Hemcinin baxHendesi silsile
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська


















